| Codeforces Beta Round 80 (Div. 1 Only) |
|---|
| Закончено |
...И пошел старик к синему морю; видит, на море черная буря. Стал он кликать золотую рыбку, но, увы, появился лишь Ктулху...
А на другом конце земного шара Пентагон уже вовсю собирает данные, прогнозирует поведение монстра и готовит сверхсекретное супероружие. Из-за высокой сейсмической активности и плохих погодных условий до сих пор не удалось сделать качественные фотоснимки со спутников. Результатом первичного анализа объекта оказался неориентированный граф c n вершинами и m ребрами. Теперь лучшим умам мира предстоит определить, можно ли считать этот граф Ктулху или нет.
Для простоты предположим, что Ктулху из космоса выглядит как некоторое сферическое тело, к которому прикреплены отростки-щупальца. Формально, Ктулху назовем такой неориентированный граф, который может быть представлен как набор из трех или более корневых деревьев, корни которых соединены простым циклом.
Гарантируется, что граф не содержит кратных ребер и петель.

В первой строке даны два целых числа — количество вершин n и количество ребер m графа (1 ≤ n ≤ 100, 0 ≤ m ≤ 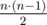 ).
).
В каждой из последующих m строк записаны пары целых чисел x и y, которые обозначают существование ребра между вершинами x и y в графе (1 ≤ x, y ≤ n, x ≠ y). Гарантируется, что граф не содержит кратных ребер и петель.
Выведите «NO», если граф не является Ктулху, и «FHTAGN!» в противном случае.
6 6
6 3
6 4
5 1
2 5
1 4
5 4
FHTAGN!
6 5
5 6
4 6
3 1
5 1
1 2
NO
Простым циклом назовем множество из v вершин, которые можно пронумеровать так, что будут существовать ребра только между вершинами с номерами 1 и 2, 2 и 3, ..., v - 1 и v, v и 1.
Дерево — связный неориентированный граф из n вершин и n - 1 ребер (n > 0).
Корневое дерево — дерево, в котором выделена одна вершина, корень.
| Название |
|---|




