Точка принадлежит треугольнику, если она лежит в треугольнике или на его границе. Два треугольника не пересекаются, если на плоскости нет точки, принадлежащей обоим треугольникам.
Вам даны $$$n$$$ точек на плоскости. Никакие две из них не совпадают, никакие три не лежат на одной прямой.
Найдите количество различных способов выбрать два непересекающихся треугольника с вершинами в данных точках. Два способа, отличающиеся только перестановкой первого и второго треугольника или перестановкой вершин в треугольниках считаются одинаковыми.
Первая строка содержит одно целое число $$$n$$$ ($$$6 \le n \le 2000$$$) — количество точек.
Каждая из следующих $$$n$$$ строк содержит два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$|x_i|, |y_i| \le 10^9$$$) — координаты очередной точки.
Никакие две точки не совпадают, никакие три точки не лежат на одной прямой.
Выведите одно целое число — количество способов выбрать два непересекающихся треугольника.
6
1 1
2 2
4 6
4 5
7 2
5 3
6
7
0 -1000000000
-5 -5
5 -5
-5 0
5 0
-2 2
2 2
21
В первом примере есть шесть пар непересекающихся треугольников, они показаны на рисунке ниже.
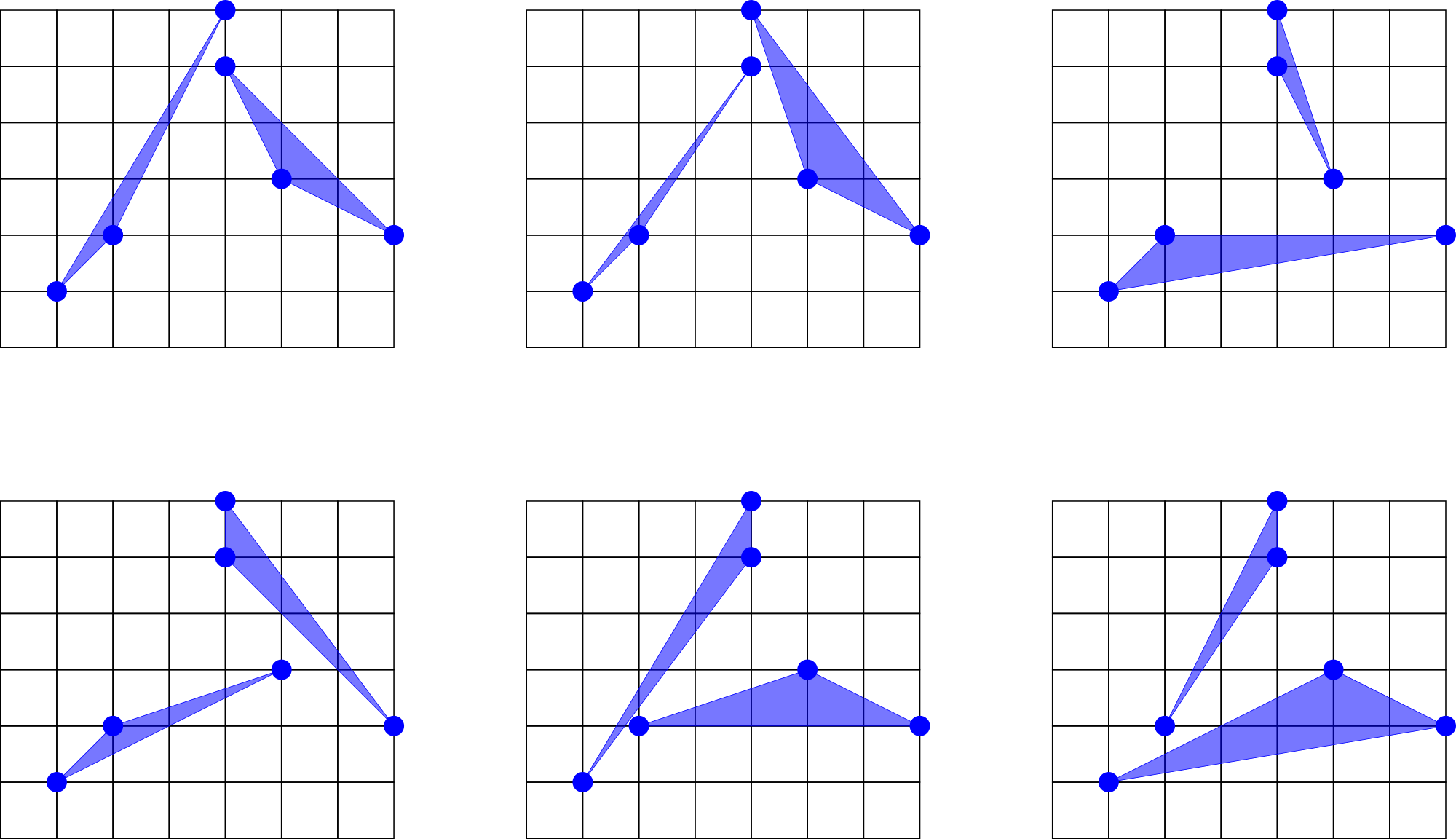
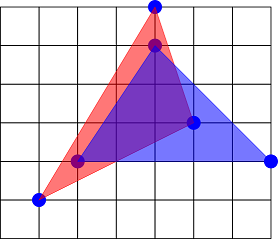
Остальные пары треугольников пересекаются, например так:
| Название |
|---|




