Группа исследователей изучает популяцию рыб в естественной системе рек и озер. Система состоит из $$$n$$$ озёр, соединённых между собой $$$n - 1$$$ реками. Каждая река имеет целочисленную длину (в километрах) и допускает перемещение в обоих направлениях. От любого озера можно добраться до любого другого по рекам (иными словами, система представляет собой дерево).
В озёрах живёт неизвестное количество рыб, неотличимых друг от друга. В день $$$1$$$ рыбы произвольно распределены по озёрам. Рыбы могут перемещаться между озёрами по рекам. Рыба может проплыть реку длиной $$$l$$$ километров за $$$l$$$ дней. Также любая рыба, которая посещает какое-либо озеро, может оставаться в нём любое количество дней. В наблюдаемый период в системе не появляется новых рыб, и присутствующие рыбы не исчезают. В любом озере в любой момент времени может находиться сколь угодно большое количество рыб одновременно.
Исследователи провели несколько наблюдений. $$$j$$$-е из этих наблюдений определило, что в день $$$d_j$$$ в озере $$$p_j$$$ находилось не менее $$$f_j$$$ различных рыб. Помогите исследователям определить наименьшее возможное общее количество рыб, проживающих в озёрах, которое не противоречило бы сделанным наблюдениям.
В первой строке записано одно целое число $$$n$$$ ($$$1 \leq n \leq 10^5$$$) — количество озёр в системе.
Следующие $$$n - 1$$$ строк описывают реки. В $$$i$$$-й из этих строк записано три целых числа $$$u_i$$$, $$$v_i$$$, $$$l_i$$$ ($$$1 \leq u_i, v_i \leq n$$$, $$$u_i \neq v_i$$$, $$$1 \leq l_i \leq 10^3$$$) — номера озёр (в нумерации с $$$1$$$), соединённых $$$i$$$-й рекой, и длина этой реки.
Следующая строка содержит одно целое число $$$k$$$ ($$$1 \leq k \leq 10^5$$$) — количество наблюдений.
Следующие $$$k$$$ описывают наблюдения. В $$$j$$$-й из этих строк записано три целых числа $$$d_j$$$, $$$f_j$$$, $$$p_j$$$ ($$$1 \leq d_j \leq 10^8$$$, $$$1 \leq f_j \leq 10^4$$$, $$$1 \leq p_j \leq n$$$) — номер дня, количество замеченных рыб и номер озера для $$$j$$$-го наблюдения. Никакие два наблюдения не были сделаны в один и тот же день в одном и том же озере одновременно.
Выведите одно число — наименьшее общее количество рыб, не противоречащее наблюдениям.
4
1 2 1
1 3 1
1 4 1
5
1 1 2
1 1 3
2 2 1
3 1 4
3 1 2
2
5
1 2 1
1 3 1
1 4 1
1 5 1
4
1 1 2
2 1 3
3 1 4
4 1 5
2
5
2 5 1
5 1 1
2 4 1
5 3 3
6
5 2 4
2 1 1
2 1 3
2 2 4
4 7 5
4 1 2
10
В первом примере одна из рыб могла проплыть через озёра $$$2$$$, $$$1$$$ и $$$4$$$, а вторая — через озёра $$$3$$$, $$$1$$$ и $$$2$$$.
Во втором примере одна рыба не могла быть замечена во всех наблюдениях одновременно, но две рыбы, плывущие по маршрутам $$$2 \to 1 \to 4$$$ и $$$3 \to 1 \to 5$$$, могли.
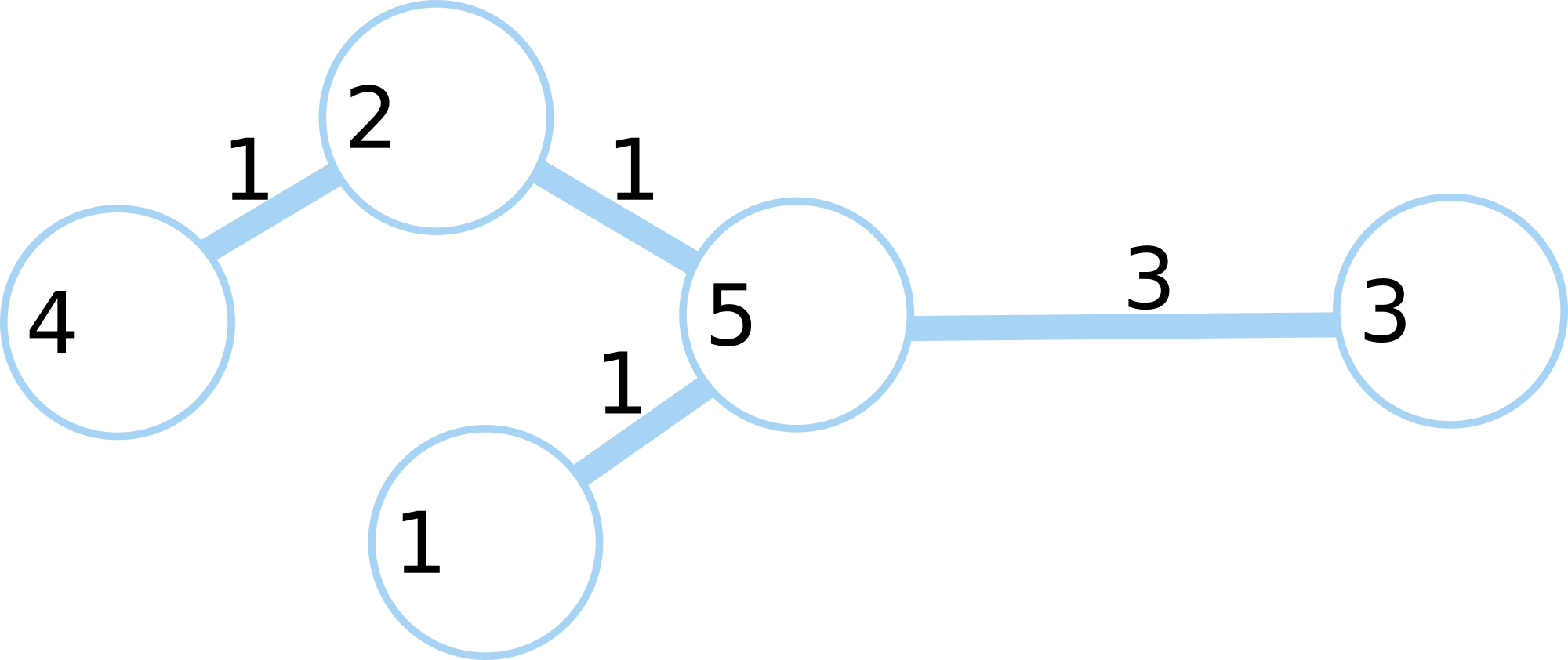
В третьем примере одна рыба могла приплыть из озера $$$1$$$ в озеро $$$5$$$, а остальные могли все время находиться в одном и том же озере: две рыбы в озере $$$4$$$, шесть рыб в озере $$$5$$$, одна рыба в озере $$$3$$$. Система озер показана на рисунке ниже.
| Название |
|---|




