F. Дерево
ограничение по времени на тест
7 секунд
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

На Марсе растёт Главное Марсианское Дерево. Оно представляет собой бинарное дерево (корневое дерево, у каждой вершины которого не более двух сыновей) с $$$n$$$ вершинами, корнем которого является вершина с номером $$$1$$$. Его плодами являются Главные Марсианские Фрукты. Сейчас лето, поэтому на этом дереве ещё нет фруктов.

Скоро наступит осень, и у дерева начнут опадать листья и ветки. Понятно, что если у дерева после этого нет какой-то вершины, то и всего её поддерева тоже нет. Кроме того, корень дерева должен остаться. Формально: у дерева останется некоторое связное подмножество вершин, содержащее корень.

После этого у дерева (в тех вершинах, которые остались) появятся плоды. В корне будет расти ровно $$$x$$$ плодов. Количество плодов в каждой оставшейся вершине не меньше, чем сумма количеств плодов в оставшихся сыновьях этой вершины. Допустимо, что в некоторых вершинах плодов не появится.

Наташе интересно, сколько вариантов деревьев может быть после описанных изменений. Поскольку это количество вариантов может быть очень большим, выведите его по модулю $$$998244353$$$.

Два варианта получившегося дерева считаются разными, если выполняется одно из двух условий:

  • в них остались разные подмножества вершин;
  • в них осталось одинаковое подмножество вершин, и есть вершина из этого подмножества, для которой количество фруктов в ней в одном варианте дерева не совпадает с количеством фруктов в ней в другом варианте дерева.
Входные данные

Первая строка содержит два целых числа: $$$n$$$ и $$$x$$$ ($$$1 \le n \le 10^5$$$, $$$0 \le x \le 10^{18}$$$) — размер дерева и количество фруктов в корне.

$$$i$$$-я из следующих $$$(n-1)$$$ строк содержит два целых числа $$$a_i$$$ и $$$b_i$$$ ($$$1 \le a_i, b_i \le n$$$) — вершины, которые соединяет $$$i$$$-е ребро дерева.

Гарантируется, что входные данные задают корректное бинарное дерево с корнем в вершине $$$1$$$.

Выходные данные

Выведите одно число — количество вариантов получившегося дерева по модулю $$$998244353$$$.

Примеры
Входные данные
3 2
1 2
1 3
Выходные данные
13
Входные данные
2 5
1 2
Выходные данные
7
Входные данные
4 10
1 2
1 3
3 4
Выходные данные
441
Примечание

Рассмотрим первый тестовый пример.

В вершине $$$1$$$ находятся $$$2$$$ фрукта. Возможны такие $$$13$$$ вариантов:

  • вершины $$$2$$$ нет, вершины $$$3$$$ нет;
  • вершины $$$2$$$ нет, в вершине $$$3$$$ нет фруктов;
  • вершины $$$2$$$ нет, в вершине $$$3$$$ есть $$$1$$$ фрукт;
  • вершины $$$2$$$ нет, в вершине $$$3$$$ есть $$$2$$$ фрукта;
  • в вершине $$$2$$$ нет фруктов, вершины $$$3$$$ нет;
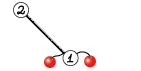
  • в вершине $$$2$$$ нет фруктов, в вершине $$$3$$$ нет фруктов;
  • в вершине $$$2$$$ нет фруктов, в вершине $$$3$$$ есть $$$1$$$ фрукт;
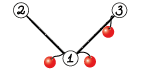
  • в вершине $$$2$$$ нет фруктов, в вершине $$$3$$$ есть $$$2$$$ фрукта;
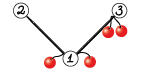
  • в вершине $$$2$$$ есть $$$1$$$ фрукт, вершины $$$3$$$ нет;
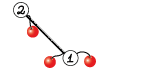
  • в вершине $$$2$$$ есть $$$1$$$ фрукт, в вершине $$$3$$$ нет фруктов;
  • в вершине $$$2$$$ есть $$$1$$$ фрукт, в вершине $$$3$$$ есть $$$1$$$ фрукт;
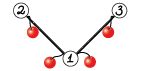
  • в вершине $$$2$$$ есть $$$2$$$ фрукта, вершины $$$3$$$ нет;
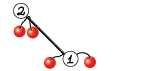
  • в вершине $$$2$$$ есть $$$2$$$ фрукта, в вершине $$$3$$$ нет фруктов.

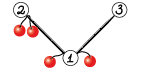
Рассмотрим второй тестовый пример. В вершине $$$1$$$ находятся $$$5$$$ фруктов. Возможны такие $$$7$$$ вариантов:

  • вершины $$$2$$$ нет;
  • в вершине $$$2$$$ нет фруктов;
  • в вершине $$$2$$$ есть $$$1$$$ фрукт;
  • в вершине $$$2$$$ есть $$$2$$$ фрукта;
  • в вершине $$$2$$$ есть $$$3$$$ фрукта;
  • в вершине $$$2$$$ есть $$$4$$$ фрукта;
  • в вершине $$$2$$$ есть $$$5$$$ фруктов.