| Codeforces Round 498 (Div. 3) |
|---|
| Закончено |
В этой задаче вам требуется помочь Берляндской армии организовать их систему распространения приказов.
Всего в Берляндской армии есть $$$n$$$ офицеров. Первый офицер — командующий армии, он не имеет никаких вышестоящих командующих. Любой другой офицер имеет ровно одного непосредственного командующего. Если офицер $$$a$$$ является непосредственным командующим офицера $$$b$$$, то можно сказать, что офицер $$$b$$$ непосредственный подчиненный офицера $$$a$$$.
Офицер $$$x$$$ является подчиненным (непосредственным или по цепочке) офицера $$$y$$$, если выполняется одно из следующих условий:
- офицер $$$y$$$ непосредственный командующий офицера $$$x$$$;
- непосредственный командующий офицера $$$x$$$ является подчиненным офицера $$$y$$$.
Например, на картинке ниже подчиненными офицера $$$3$$$ являются: $$$5, 6, 7, 8, 9$$$.
Структура Берляндской армии организована таким образом, что каждый офицер, кроме командующего, является подчиненным командующего армией.
Формально, Берляндская армия может быть представлена как дерево, состоящее из $$$n$$$ вершин, в котором вершина $$$u$$$ соответствует офицеру с номером $$$u$$$. Предок вершины $$$u$$$ соответствует непосредственному командующему офицера $$$u$$$. Корень (который имеет номер $$$1$$$) соответствует командующему армией.
Военное министерство Берляндии приказало вам ответить на $$$q$$$ запросов, $$$i$$$-й запрос представлен в виде $$$(u_i, k_i)$$$, где $$$u_i$$$ — это некоторый офицер, а $$$k_i$$$ — некоторое натуральное число.
Для обработки $$$i$$$-го запроса представим, как приказ, отданный офицером с номером $$$u_i$$$ распространяется по поддереву $$$u_i$$$. Этот алгоритм очень похож на DFS (depth first search, обход в глубину).
Представим, что сейчас распространяет приказ офицер с номером $$$a$$$. Офицер $$$a$$$ выбирает $$$b$$$ — одного из своих непосредственных подчиненных (то есть сына в дереве), который еще не получил приказ. Если существует несколько таких непосредственных подчиненных, тогда $$$a$$$ выбирает офицера с минимальным индексом среди них. Офицер $$$a$$$ отдает приказ офицеру $$$b$$$. После этого $$$b$$$ использует такой же самый алгоритм, чтобы распространить приказ в своем поддереве. После того, как $$$b$$$ прекращает распространять приказ, офицер $$$a$$$ выбирает следующего непосредственного подчиненного (при помощи такого же алгоритма). Когда $$$a$$$ не может выбрать непосредственного подчиненного, еще не получившего приказ, офицер $$$a$$$ прекращает распространять приказ.
Посмотрим на следующий пример:
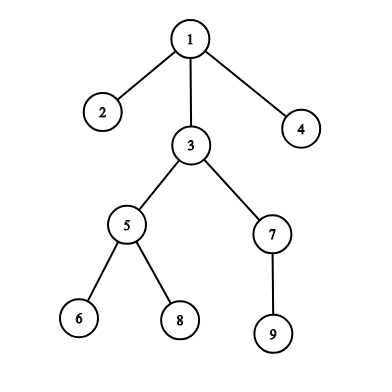
Если офицер $$$1$$$ распространяет приказ, офицеры в его поддереве получат приказ в следующем порядке : $$$[1, 2, 3, 5 ,6, 8, 7, 9, 4]$$$.
Если офицер $$$3$$$ распространяет приказ, офицеры в его поддереве получат приказ в следующем порядке: $$$[3, 5, 6, 8, 7, 9]$$$.
Если офицер $$$7$$$ распространяет приказ, офицеры в его поддереве получат приказ в следующем порядке: $$$[7, 9]$$$.
Если офицер $$$9$$$ распространяет приказ, офицеры в его поддереве получат приказ в следующем порядке: $$$[9]$$$.
Чтобы ответить на $$$i$$$-й запрос $$$(u_i, k_i)$$$, сформируем последовательность того, в каком порядке офицеры будут получать приказ, если $$$u_i$$$-й офицер начал его распространять. Ответом будет являться $$$k_i$$$-й элемент сформированной последовательности или -1, если в ней меньше $$$k_i$$$ элементов.
Запросы необходимо рассматривать независимо. Запрос не затрагивает следующие запросы.
Первая строка входных данных содержит два целых числа $$$n$$$ и $$$q$$$ ($$$2 \le n \le 2 \cdot 10^5, 1 \le q \le 2 \cdot 10^5$$$) — количество офицеров в Берляндской армии и количество запросов.
Вторая строка входных данных содержит $$$n - 1$$$ целое число $$$p_2, p_3, \dots, p_n$$$ ($$$1 \le p_i < i$$$), где $$$p_i$$$ — номер офицера, являющегося непосредственным командующим офицера с номером $$$i$$$. Командующий армией имеет номер $$$1$$$ и не имеет непосредственного командующего.
Следующие $$$q$$$ строк описывают запросы. Запрос с номером $$$i$$$ описан парой ($$$u_i, k_i$$$) ($$$1 \le u_i, k_i \le n$$$), где $$$u_i$$$ — номер офицера, который начинает распространять приказ, и $$$k_i$$$ — позиция требуемого офицера в порядке распространения приказа.
Выведите $$$q$$$ чисел, где $$$i$$$-е число — это офицер на позиции $$$k_i$$$ в порядке распространения приказа в поддереве офицера $$$u_i$$$, если распространение приказа начинается с него. Выведите "-1", если количество офицеров, получивших приказ, меньше $$$k_i$$$.
Запросы необходимо рассматривать независимо. Они не влияют друг на друга.
9 6
1 1 1 3 5 3 5 7
3 1
1 5
3 4
7 3
1 8
1 9
3
6
8
-1
9
4
| Название |
|---|




