| Codeforces Beta Round 10 |
|---|
| Закончено |
Залы всех кинотеатров Берлядии представляют собой прямоугольники в K рядов по K кресел в каждом, причем K — нечетное число. Ряды и места нумеруются с 1 до K. Из соображений безопасности, человек, пришедший в кассу за билетами, не может сам выбрать места. Раньше это делал кассир, а теперь этим будет заниматься специальная программа рассадки. Было выяснено, что подавляющее большинство жителей Берляндии в кинотеатре предпочитают смотреть фильм, поэтому хотят сидеть как можно ближе к центру зала. Кроме того, компания из M человек, желающая посмотреть фильм, хочет непременно занять M последовательных мест в одном ряду. Сформулируем алгоритм, в соответствии с которым программа выдает людям билеты. При поступлении запроса на M мест программа должна определить номер ряда x и отрезок [yl, yr] номеров кресел на этом ряду, причем yr - yl + 1 = M. Из всех таких возможных вариантов программа должна выдать тот, для которого значение функции суммарной удаленности от центра минимально. Пусть 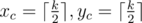 — номер ряда и номер места у самого "центрального" кресла. Тогда значением функции удаленности от центра зала будет
— номер ряда и номер места у самого "центрального" кресла. Тогда значением функции удаленности от центра зала будет 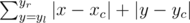 . Если вариантов с минимальным значением этой функции несколько, то программа должна выдать тот, что ближе к экрану (т.е. номер ряда x меньше). Если же вновь имеется неоднозначность, следует выдать вариант с минимальным yl. Если вы еще не догадались, то ваша задача — промоделировать работу программы.
. Если вариантов с минимальным значением этой функции несколько, то программа должна выдать тот, что ближе к экрану (т.е. номер ряда x меньше). Если же вновь имеется неоднозначность, следует выдать вариант с минимальным yl. Если вы еще не догадались, то ваша задача — промоделировать работу программы.
Первая строка содержит два целых числа N и K (1 ≤ N ≤ 1000, 1 ≤ K ≤ 99) — число запросов и размер зала соответственно. Во второй строке содержится N целых чисел Mi из диапазона [1, K], разделенных пробелами, — запросы к программе.
Выведите N строк. В i-й строке выведите «-1» (без кавычек), если невозможно найти Mi свободных подряд идущих кресел в одном ряду, или выведите тройку x, yl, yr в противном случае. Числа разделяйте пробелами.
2 1
1 1
1 1 1
-1
4 3
1 2 3 1
2 2 2
1 1 2
3 1 3
2 1 1
| Название |
|---|




