I participated in this year's Facebook Hacker Cup and have enjoyed all the problems so far. The only problem I couldn't solve during the contest was the last problem of Round 2 named "Seafood" (link). Facebook always uploads solutions right after the contest, which I'm thankful for, so I checked the solution for that problem. However, I couldn't see why the solution works just from their description. Maybe I'm not thinking through it enough, but I found it hard to justify their approach in mathematical rigor. So I picked up key ideas from their description and filled out the details. I'm writing this for myself, and it turns out to be more complicated than I thought but I hope this helps some folks out there. If you have any simpler solution/description I'm happy to know.
Here is a short synopsis of the problem. You start at position $$$0$$$ of a number line and move around. There are clams and rocks on the number line. Each clam/rock have distinct positive coordinates and also its own strength as a number. When you are on a position where a clam is placed, you can take the clam immediately and you can hold multiple clams at a time. When you are on a position where a rock is placed, you can use the rock to break open any clam you have with lesser strength. Your goal is to open all the clams in minimum distance moved (or determine that you can't). You should do this in quasilinear time over the number of clams+rocks.
Some facts were evident. For example, there is no harm at picking clams as soon as we meet them. Also, we may assume that the rocks we use decrease in strength, because if we planned to use stronger rock later we can actually skip the weaker one and open the clams with stronger one later. However, this observation turned out to be a red herring as we don't use this assumption in the solution below.
If we move in the left direction on an optimum path, I thought it is because there is a rock we have to use even if we pay the cost of moving back and then forward without getting any clams. With this, one thing that recurred in my mind was that the optimum path should have a particular shape. For example, if this is one possible path
--------------->
x<-------
------------->
x<-------
----------------->
where 'x' denotes the stone we use, there seemed no reason to use two overlapping intervals and we can just use
-------------------->
x<---x--------
---------------------->
instead. With this, my idea was that the optimum path consists of such disjoint 'Z-shaped' overlapping intervals, ending with
-------------------->
or
-------------------->
x<------------
But I couldn't justify any of them formally nor use these observations to find an effective algorithm. In particular, how can we determine where does the path end and how far does the path extend? At that time I felt damn sleepy (after 3 hours of contest it was 5AM here) and gave up. Fortunately I finished at around 160-ish and get the T-shirt and so.
The optimum path should turn its direction or end where either a clam or rock is, or we waste some distance in the middle. Call any interval with endpoints at 0/clam/rocks with no clams nor rocks inside a simple interval. An optimal path will consist of sequence of simple intervals with directions. We will use this observation later.
The optimum path should extend to at least the rightmost clam $$$c_r$$$ because we have to pick it. As soon as we pick $$$c_r$$$, we have collected all the clams so the only thing left to do is to find the rock that opens all the collected yet unopened clams. Therefore, the optimum path will (i) visit $$$c_r$$$ and (ii) move in shortest distance to a rock $$$e$$$ that opens all remaining clams and end. The first key is to assume that we know $$$e$$$ in prior. This takes a bit of courage, but it will completely determine the optimum path and enable us to compute the optimum path effectively. Say the rightmost position we visit is $$$r$$$. We have $$$r = \max(c_r, e)$$$.
The second key is to distinguish between clams that are 'naturally' opened during the journey and clams that need to be carried back(left) to open. Fix arbitrary clam $$$c$$$. (a) If there is a stronger rock $$$r_c$$$ in between $$$c$$$ and $$$r$$$ (inclusive) we will eventually hit $$$r_c$$$ after picking $$$c$$$ by mean value theorem so there is no need to worry about $$$c$$$. (b) Otherwise, we should reach $$$c$$$ to pick and then move to left to find any stronger rock (if exists).
Discard clams of case (a) and for any clam $$$c$$$ of case (b), let's compute the rightmost rock $$$r_c$$$ that is stronger than $$$c$$$, which should be on the left side of $$$c$$$. Then an optimal path sweep through any simple interval inside $$$I_c = [r_c, c]$$$ from right to left at some moment to carry $$$c$$$ to $$$r_c$$$. Take union over such $$$I_c$$$'s and call the union $$$S$$$. Then we see that a simple interval in $$$S \cap [0, e]$$$ has to be swept at least three times (right, then left because the interval is in $$$S$$$, then right to finish at $$$e$$$). All the other simple intervals in $$$[0, e]$$$ has to be swept at least one time (from left to right) and intervals in $$$[e, r]$$$ at least two times (to visit $$$r$$$ and finish at $$$e$$$). This gives an lower bound on the path length; for each simple interval in between $$$[0, r]$$$, multiply its length with its multiplicity and sum over.
Is the lower bound attainable? Yes: Say $$$S = \cup_i [a_i, b_i]$$$ where $$$[a_i, b_i]$$$ are disjoint maximal intervals inside $$$S$$$, ordered so that $$$a_1 < b_1 < a_2 < b_2 < \cdots$$$. Start moving from 0 to right. For each interval $$$[a_i, b_i]$$$ with $$$b_i \leq e$$$, go to $$$b_i$$$ then move back to $$$a_i$$$ and then move in right direction again. Do this in the increasing order of $$$i$$$. After all such intervals are processed, keep moving until we hit $$$r$$$. From $$$r$$$, if the unique interval $$$[a_i, b_i]$$$ such that $$$a_i < e < b_i$$$ exists, move to $$$a_i$$$ and then $$$e$$$. Otherwise, move from $$$r$$$ to $$$e$$$ directly. By definition this path attains the multiplicity bound described in previous paragraph. Also, this path sweeps each $$$[a_i, b_i]$$$ from right to left at some point, so all clams $$$c$$$ are carried to $$$r_c$$$ as $$$[r_c, c] \subseteq [a_i, b_i]$$$ for some $$$i$$$. Therefore, we have found the optimum path assuming the value of $$$e$$$.
It only remains to compute $$$S$$$ (the multiplicity of each simple interval) effectively as we change over $$$e$$$. Iterate $$$e$$$ over all rocks from right to left. As $$$e$$$ moves from right to left, intervals of form $$$[r_c, c]$$$ only adds up, so as one interval $$$I = [r_c, c]$$$ forms we can just update $$$S$$$ by $$$S := S \cup I$$$. This can be done effectively by various means (maintain $$$S$$$ or its complement as std::set, union-find, etc). For each update, observe the simple intervals added to $$$S$$$ and update the length of optimum path. As each simple interval adds to $$$S$$$ at most once, the total time taken is the number of simple interval times multiplied by time taken for adding an interval to $$$S$$$. This makes the total time quasilinear over the number of clams/rocks (I'm being sketchy here. Please let me know if you want the details).
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <set>
#include <string>
using namespace std;
long long solve(int n,
vector<int> p,
vector<int> h,
const string &s);
int main() {
int T;
scanf("%d", &T);
for (int t = 1; t <= T; t++) {
int n;
scanf("%d", &n);
long long a, b, c, d;
vector<int> p(n);
scanf("%d %d %lld %lld %lld %lld", &p[0], &p[1], &a, &b, &c, &d);
for (int i = 2; i < n; i++)
p[i] = ((a * p[i - 2] + b * p[i - 1] + c) % d) + 1;
vector<int> h(n);
scanf("%d %d %lld %lld %lld %lld", &h[0], &h[1], &a, &b, &c, &d);
for (int i = 2; i < n; i++)
h[i] = ((a * h[i - 2] + b * h[i - 1] + c) % d) + 1;
string s;
cin >> s;
printf("Case #%d: %lld\n", t, solve(n, p, h, s));
}
return 0;
}
struct thing {
int p, h;
char t;
int data;
thing() {}
thing(int p, int h, char t) : p(p), h(h), t(t) {}
};
const int tmax = 1048575;
const int inf = 1000000000;
struct FenwickTree {
int tree[tmax + 1];
void clear() {
for (int i = 1; i <= tmax; i++)
tree[i] = -inf;
}
FenwickTree() {
clear();
}
void upd(int i, int val) {
i++;
while (i <= tmax) {
tree[i] = max(tree[i], val);
i += (i & -i);
}
}
int calc(int i) {
i++;
if (i <= 0)
return -inf;
assert(1 <= i && i <= tmax);
int res = tree[i];
while (i > 0) {
res = max(res, tree[i]);
i -= (i & -i);
}
return res;
}
};
struct IntervalUnion {
set<int> complement;
vector<int> weights;
long long weight = 0LL;
IntervalUnion(vector<int> w) : weights(w) {
for (int i = 0; i <= tmax; i++)
complement.insert(i);
}
void add(int i, int j) {
auto l = complement.lower_bound(i);
auto u = complement.lower_bound(j);
for (auto it = l; it != u; it++) {
weight += weights[*it];
}
complement.erase(l, u);
}
bool subtract(int i) {
if (complement.count(i) == 0) {
complement.insert(i);
weight -= weights[i];
return true;
} else {
return false;
}
}
};
vector<int> pivots[tmax];
long long solve(
int n,
vector<int> p,
vector<int> h,
const string &s) {
vector<thing> things(n);
for (int i = 0; i < n; i++)
things[i] = thing(p[i], h[i], s[i]);
sort(things.begin(), things.end(), [](const thing &t1, const thing &t2) {
return t1.p < t2.p;
});
sort(h.begin(), h.end());
h.resize(unique(h.begin(), h.end()) - h.begin());
for (auto &t : things) {
t.h = lower_bound(h.begin(), h.end(), t.h) - h.begin();
t.h = int(h.size()) - 1 - t.h;
}
FenwickTree ft;
for (int i = 0; i < n; i++) {
if (things[i].t == 'R') {
ft.upd(things[i].h, i);
} else {
things[i].data = ft.calc(things[i].h - 1);
}
}
vector<int> weights(n);
for (int i = 0; i < n; i++)
weights[i] = things[i].p - (i == 0 ? 0 : things[i - 1].p);
IntervalUnion iu(weights);
ft.clear();
for (int i = 0; i <= tmax; i++)
pivots[i].clear();
for (int i = n - 1; i >= 0; i--) {
if (things[i].t == 'R') {
ft.upd(things[i].h, -i);
} else {
int cc = ft.calc(things[i].h - 1);
if (cc == -inf) {
// no rock in forward to handle
if (things[i].data < 0)
return -1;
else {
iu.add(things[i].data + 1, i + 1);
}
} else {
assert(-cc >= 0 && -cc < n);
pivots[-cc].push_back(i);
}
}
}
long long ans = 1000000000000000000LL;
long long cans;
bool met_clam = false;
long long clam_pos = -1LL;
for (int i = n - 1; i >= 0; i--) {
if (things[i].t == 'R') {
if (!met_clam) {
cans = things[i].p + 2LL * iu.weight;
} else { // met_clam
cans = 2LL * clam_pos - things[i].p + 2LL * iu.weight;
}
ans = min(ans, cans);
} else if (!met_clam) {
met_clam = true;
clam_pos = things[i].p;
}
if (things[i].t == 'R' && !met_clam) {
for (auto clamback : pivots[i]) {
iu.add(things[clamback].data + 1, clamback + 1);
}
}
iu.subtract(i);
}
return ans;
}









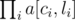 , basically because only cycles of same length interact.
, basically because only cycles of same length interact. values of
values of 
