(Context: https://codeforces.me/blog/entry/136021)
Oh, hello there! It’s me, the stuffed penguin. You might think I’m just sitting around here, looking cute with my pink feet and fluffy wings, but little do you know, I’m actually the perfect embodiment of wisdom. Or, well, that’s what I tell myself to feel better about my life of plushy leisure.
I often get teased about being “lazy, just like a segment tree.” Honestly, I don’t even mind. Have you ever seen a segment tree in action? It looks like it’s doing absolutely nothing most of the time, just like me! But when the moment calls for it, bam, it comes out of nowhere and solves complex range queries with ease. That’s kind of my approach to life: hang out, chill in my little spot, and when the time comes to be cuddled or admired, I deliver. Efficiently.
Now, let’s get one thing straight: just because I spend most of my time sitting next to this igloo house (which I rarely leave), doesn’t mean I’m not doing anything. Much like a segment tree, I’m always “ready.” In programming terms, I’m in a state of restful, pre-processed calm. You never know when you’ll need me to provide comfort or inspiration. I like to think that I’m working smarter, not harder, like a true optimization master.
So, next time you see me lounging around, remember—there’s more going on behind these plushy eyes than you think!








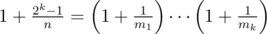 .
. 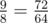 . Hmmm now how could we do this?
. Hmmm now how could we do this? 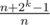 to a range
to a range 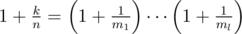 , where
, where 
