Hi! The motivation for writing this editorial is because lot of programmers were asking for explanation of solution for $$$D$$$ in comments and I was also one of them stuck in it. Since official editorial has not been published yet, I have thought of writing one.
First of all I would like to give credit to this comment by code_hard123 which was a huge help for me to solve this problem.
Editorial
Problem: Link
Let us first be clear with the fact that whenever there is cycle of odd length in a graph it can never be a bipartite graph. I recommend to read more about this if you don't understand before moving ahead. You can read it from here.
Claim: Only elements with same powers of $$$2$$$ in $$$B$$$ will form a bipartite graph. For example $$$B=(6,12)$$$ will not form a bipartite graph while $$$B=(4,12)$$$ will form one.
Proof: We can easily check if any two elements can be in $$$B$$$ at same time to form a bipartite graph. Let us consider two numbers $$$a$$$ and $$$b$$$. Then they form a cycle of length $$$\frac{lcm(a,b)}a$$$ $$$+ \frac{lcm(a,b)}b$$$.
Consider $$$a=8$$$ and $$$b=12$$$ and see following graph.
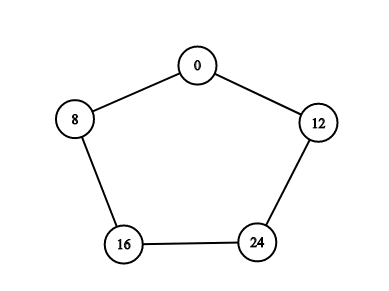
Now $$$\frac{lcm(a,b)}a$$$ $$$+ \frac{lcm(a,b)}b$$$ will be odd when $$$x\neq y$$$ where $$$a=2^x \times c$$$ and $$$b=2^y \times d$$$.
When $$$x>y$$$ then $$$\frac{lcm(a,b)}a$$$ will be $$$2^{x-x} \times e$$$ which is odd and $$$\frac{lcm(a,b)}b$$$ will be $$$2^{x-y} \times f$$$ which is even.
When $$$x<y$$$ then $$$\frac{lcm(a,b)}a$$$ will be $$$2^{y-x} \times e$$$ which is even and $$$\frac{lcm(a,b)}b$$$ will be $$$2^{y-y} \times f$$$ which is odd.
Hence, we have proved that only elements with same powers of $$$2$$$ in $$$B$$$ will form a bipartite graph.
The task is simple now. Just find highest powers of $$$2$$$ for every element in $$$B$$$. Now we keep majority elements with same power and discard the rest.
Time Complexity: $$$O(nlog(maxB))$$$
Suggestions are welcomed :)
PS: At the time of writing this editorial, the official one was already posted.











