Hello, Codeforces! new round dropping soon btw
There are ways to modify Li Chao Tree to support more powerful types of operations, some of which are already described here. This tutorial will focus on extending the aforementioned data structure to solve the following problem:
- Operation 1: Add a new line
- Operation 2: For a given point, find the line that yields the $$$k$$$-th minimum value at that point
We will assume, without loss of generality, that $$$k$$$ does not change during the queries. Our goal is to perform those operations in $$$O(k \cdot log C)$$$ each. Note that a simple Li Chao Tree solves our problem for $$$k=1$$$.
The Idea
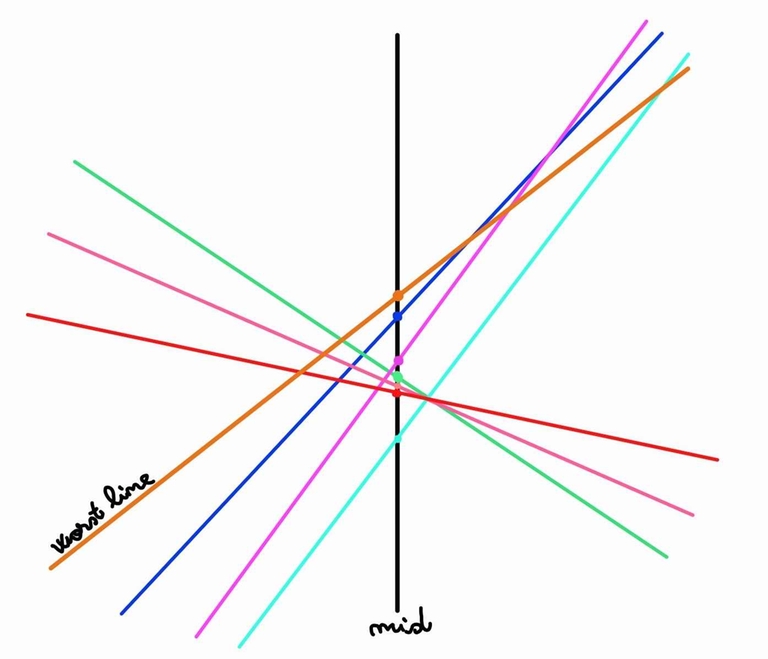
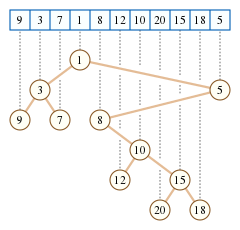
Since a normal Li Chao Tree stores the best line in each node, it is natural to think that all we need to do is to keep the best $$$k$$$ lines. ( where the best line is defined as the line that gives the minimum value when evaluated at the midpoint of the segment ).
This insight, however, proves to be only halfway right, because when popping the worst line from the set we can't really tell where to push it next because it might be useful in both halves. The fix is surprisingly simple: keep $$$2 \cdot k - 1$$$ lines instead.
Why does this work?
It turns out that the worst line will always be above any of the other $$$2 \cdot k - 1$$$ lines in either half.
Suppose it will be above $$$a$$$ lines in the first half and $$$b$$$ in the second. By the claim above, it follows that $$$a + b = 2 \cdot k - 1$$$. Thus, $$$max(a,b) \ge \lceil \frac{2 \cdot k - 1}{2} \rceil = k$$$. This essentially means that in one of the halves it can't be among the $$$k$$$ best lines since there are already $$$k$$$ lines better than it. Now, we can traverse only $$$O(logC)$$$ nodes every update.
Implementation
The overall code slightly differs from the one of a normal Li Chao Tree. To avoid an extra log factor, one could use partial sorting methods, such as nth_element in C++, which works linearly on average.
Last but not least, thanks to AlexLuchianov for helping development of this trick.
UPD: here is another discussion about this problem.