Всем привет! Хочу рассказать о достаточно простом приеме (не знаю как называется) для оптимизации динамики. Очень часто бывает так, что при пересчете нам надо искать минимум в какой-нибудь уже посчитанной таблице, но при этом игнорируя некоторое конечное количество строк и столбцов; как оптимизировать такое и подобное, описано в блоге.
Постановка задачи
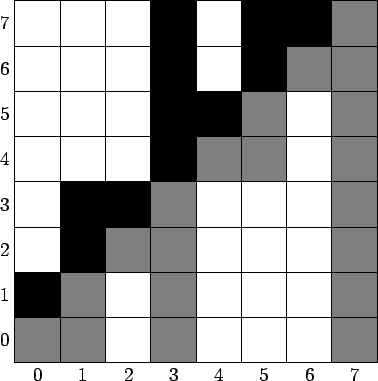
Итак, у нас есть таблица, предположим, что большая — $$$N \times N$$$, и мы хотим сделать какое-то большое количество запросов вида «Найди максимальное значение в таблице, которое не лежит в столбцах из множества $$$C$$$ и строках из множества $$$R$$$», при этом для каждого запроса гарантируется, что $$$max ( |C|, |R| ) \leq K$$$, где $$$K$$$ -- какая-то очень маленькая константа. Эту задачу мы бы могли решать, например, с помощью двумерного ДО -- но это работает долго и занимает гораздо больше памяти.
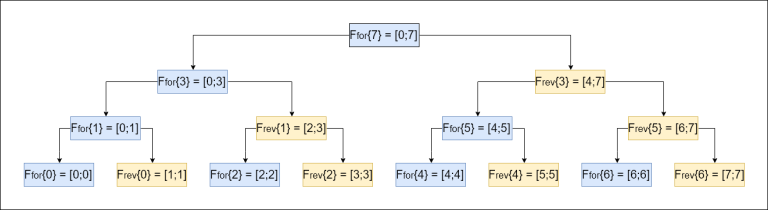
Решается задача просто, давайте для начала, найдем $$$x_1$$$ — глобальный максимум в таблице и запомним его позицию $$$(i_1, j_1)$$$. Далее, при дальнейших запросах, возможен вариант, что либо $$$i_1 \in C$$$, либо $$$j_1 \in R$$$, поэтому давайте запустим два рекурсивных вызова, с поиском максимума в таблице, в одном из них запретив строку $$$i_1$$$, а в другом -- столбец $$$j_1$$$. Таким образом каждая рекурсивная функция считает максимум, в случае, если мы запрещаем столбцы $$$C'$$$ и строки $$$R'$$$. Заметим, что при $$$C' > k$$$ и $$$R' > k$$$ значения нам считать не надо, так что можно смело обрывать рекурсию.
Чтобы в таком случае искать максимум можно просто пройтись по кандидатам $$$O(C_{2K}^K)$$$ или используя дерево рекурсивных вызовов пройтись по нему и найти максимум за $$$O(K)$$$, во всяком случае, вы понимаете, что это работает быстро. Да, кстати, по очевидным причинам алгоритм построения этой таблицы работает за $$$O(N^2 \cdot C_{2K}^K)$$$, и алгоритм является корректным. Почему? Ну потому что если вдруг глобальный максимум не будет запрещен по обоим кандидатам, то очевидно, это будет ответ на запрос, а в ином случае, если запрещена строка, в которой он находится, то в одном из рекурсивных вызовов мы посчитали другого кандидата и так далее.
Почему это бывает полезно?
Приведу пример задачи на эту тему. У нас есть дерево размером $$$N$$$, в каждой вершине которого записана буква от $$$a$$$ до $$$z$$$, назовем строку хорошей, если ни одна его подстрока длиной больше $$$1$$$ не является палиндромом. Требуется найти максимальную подпоследовательность, какого-то простого пути в дереве, такую, что если записать символы в вершинах этой последовательности, то получится хорошая строка.
Докинем в афлавит фиктивный символ $$$\epsilon$$$. За $$$\Sigma$$$ обозначим размер алфавита, в данном случае $$$\Sigma = 26 + 1$$$. Заведем трехмерную динамику $$$dp$$$ с размерностью $$$N \times \Sigma \times \Sigma$$$, в $$$dp[v][i][j]$$$ будем хранить максимальную подпоследовательность, пути идущего сверху-вниз до вершины $$$v$$$, два последних символа которой равны $$$i$$$ и $$$j$$$, $$$i=j=\epsilon$$$ значит, что строка пустая, $$$i=\epsilon$$$ значит, что строка содержит ровно один символ. Динамика очень легко пересчитывается и это суммарно отработает за $$$O(N \cdot \Sigma ^ 2)$$$. Чтобы посчитать ответ на задачу требуется перебрать LCA двух конечных вершин пути и с помощью посчитанных значений динамики найти максимальное значение $$$dp'[u][x][y] + dp[v][z][w]$$$, где $$$dp'[u]$$$ обозначает динамику $$$dp$$$, посчитанную для путей исходящих из поддерева вершины $$$u$$$ и заканчивающих свой путь в предке $$$u$$$, при этом $$$u$$$ и $$$v$$$ -- братья и при этом $$$y \neq z$$$, $$$y \neq w$$$, $$$x \neq z$$$. При этом такой максимум уже можно найти за $$$O(N{\Sigma}^4)$$$, это медленно.. Можно постараться и найти его за $$$O(N{\Sigma}^3)$$$. Но с помощью структуры данных, описанных выше это можно сделать тривиальным образом за $$$O(N{\Sigma}^2)$$$.
Кстати, с помощью нашей структуры данных можно пойти гораздо дальше. Можно сказать, что все состояния динамики нам совершенно не нужны. Давайте вместо трехмерной динамики $$$dp$$$ построим динамику $$$dc$$$ размера $$$N$$$, основанную на CandidateSet, в котором есть не более одного запрета $$$x$$$ и не более двух запретов на $$$y$$$, для каждого состояния исходной динамики. Пересчитывать ее очень просто и приятно -- это работает за $$$O(N)$$$, единственная вещь, которую я не описал -- это объединение множества кандидатов и его обрезание, но я верю в то, что вы и сами справитесь :D. Утверждается, что глобальный максимум по $$$dp'[u][x][y] + dp[v][z][w]$$$ достигается и среди сумм $$$dc'[u][x][y] + dc[v][x][y]$$$, определенных по такому же принципу. Доказать это очень просто, пусть это останется как упражнение читателю, но с помощью этого простого трюка наше решение превращается в гордый $$$O(N)$$$ с большой константой. Ура!