Let n is a positive integer.
n = p1e1p2e2...pkek is the complete prime factorization of n.
Let me define a function f(n)
f(n) = p1c1p2c2...pkck where ck = ek if ek is divisible by pk, otherwise ck = ek - 1
Example:
72 = 2332, so f(72) = 23 - 132 - 1 = 2231 = 12
144 = 2432, so f(144) = 2432 - 1 = 2431 = 48, as 4 is divisible by 2, exponent of 2 remains same.
Now let
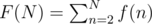
Example: F(10) = 1 + 1 + 4 + 1 + 1 + 1 + 4 + 3 + 1 = 17
Now I want to evaluate F(N) for a fairly large value of N, say 1014. Can I do it without factorizing each number?
It is more difficult than the previous one.










