Hello!
My question is simple. Can someone give me a test sample for maximum matching in bipartite graphs on which Kuhn's algorithm preforms badly (something like O(N * M) in time). Thanks in advance.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 154 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
Hello!
My question is simple. Can someone give me a test sample for maximum matching in bipartite graphs on which Kuhn's algorithm preforms badly (something like O(N * M) in time). Thanks in advance.
Hello!
Some time ago I thought of the following problem:
We have a bracket sequence with length n (n ≤ 105) and we have q (q ≤ 105) queries for finding the length of the longest correct bracket substring (with consecutive elements) in a interval [l;r] (1 ≤ l ≤ r ≤ n).
Sample:
6
((()()
3
1 6 -> Answer is 4 (substring from 3rd to 6th position)
1 2 -> There is no correct bracket substring so the answer is 0
1 4 -> Answer is 2 (substring from 3rd to 4th position)
So I found a 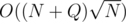 solution with MO's algorithm but I am curious if there is an online solution. So if anyone has one, please share it. Thanks in advance.
solution with MO's algorithm but I am curious if there is an online solution. So if anyone has one, please share it. Thanks in advance.
Hello everyone!
Today I was solving a problem and I reduced it to finding a maximum of a function. So in short what I need is the following:
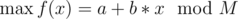 , where M, a, b ≤ 109.
, where M, a, b ≤ 109.
It's obvious that 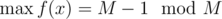 iff
iff 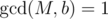 , but I cannot find an easy way to get the maximum if
, but I cannot find an easy way to get the maximum if 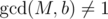 . I will appreciate any help on the problem.
. I will appreciate any help on the problem.
PS: a, b and M are given as queries so I need an algorithm to answer up to 105 queries.
UPDATE: It's actually pretty simple. 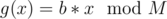 actually has values of form
actually has values of form 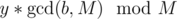 . Then it's obvious that the solution will be
. Then it's obvious that the solution will be 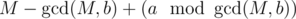 .
.
Hello everyone!
I was solving a problem (from a Bulgarian competition) which is about the game Lights Out — https://en.m.wikipedia.org/wiki/Lights_Out_(game). In the problem you are given a NxM table (N*M<=1000) — the initial configuration of the game. You whant to make all the cells equal to zero. You should print a way to do this.
The problem can be solved with meet in the middle and bitmask dp, with the given constraints. Another way is using Gauss elimination modulo 2 with N*M equations for each cell. But this approach is O((N * M)3). It actually can be reduced to 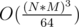 with a bitset.
with a bitset.
In the editorial of the problem it is said that there exists a solution for much larger data — N,M<=500, using Gauss elimination but it isn't explained. If someone knows it can he/she explain it. I will appreciate your help!
I decided to look the new blog posts on codeforces. I logged in and saw that I'm a candidate master but with 1899 rating. After failing yesterday's contest because of bug in my Div2 E, I ended 243. So my rating increased by +7. But it was shown that I'm expert with 1906 rating.
So now what is my current rating 1899 or 1906, because I'm curious if I can participate in the today's codeforces round.
PS: I also saw that a couple of my submissions are gone (the last ones).
Hello!
Today, at 08:00 UTC will be held Deadline24's qualifying round.
Let's discuss problems here, after the contest of course!
Hello!
I was solving problem Minxor from second day of RMI 2014. In short the problem is:
You have 3 types of queries.
1 x -> inserts x into the set
2 x -> deletes x from the set
3 -> asks for the smallest xor of any two numbers in the set
I solved the problem offline using a trie + divide and conquer. My solution is similar to link. Again in short: compressing all updates as "number x appears from time I to time J". Here is the code. The complexity is O(M * log(M) * 32);
So my question is:
Is there a solution which runs faster than that or/is online. Thanks in advance :)
While solving Goodbye 2015, E i was getting TL on test 11. Now after the contest I decided to see what was the problem.
After some debugging I found that when you do lower bound on an empty set it gives TL:
http://codeforces.me/contest/611/submission/15127498 — AC
http://codeforces.me/contest/611/submission/15126396 — TL11
The only difference is if(s.size() == 0) break;
So I want to ask if there are similar issues with the std::set.
PS: This was a good lesson for me. Next time I wont try debugging one solution for 2 hours and will solve the other problems.
Hello codeforces,
I was solving this problem:
You are given a graph, and you have to answer queries of type:
1) Delete edge from U to V
2) Add edge from U to V
3) See if vertexes U and V are in the same connected component.
I couldn't come with an online solution, but I think I found an offline one.
So first I compress all queries of adding or removing and edge as: edge from U to V is available in time [i; j], where i is the time of adding and j is time of removing. Now we can do divide and conquare with dsu. This will be like that:
Rec(L, R, dsu)
{
Look for all queries that are q.L <= L and R <= q.R
([L; R] lies in [q.L; q.R]) and add unite q.U and q.V in dsu
IF L == R -> if query[L] is of type 3 then answer it and stop (and also undo changes to dsu).
Mid = (L + R) / 2;
Rec(L, Mid, dsu);
Rec(Mid + 1, R, dsu);
Undo changes to dsu
}
So this solution is O(M*logM*Cost_of_dsu). But the problem is in the DSU (the undoing of operations). I couldn't find how to do persistent DSU or DSU with restoring/undoing/backtracking. So if someone knows how to do this I will really appriciate if he helps! :)
PS: By DSU I mean disjoint set union
Hello codeforces,
I was solving IZHO problems from past years but I couldn't solveIZHO 201problem E — "K blocks" (link; the second problem). I wrote the O( N * N * K ) dp solution, but I'm not sure how to reduce it to O( N * K ). I tought of Convex hull trick, but unfortunately i don't know how to apply it.
So can someone share his solution? Thanks ;)
On 25-26 April The Bulgarian National Olympiad in Informatics took place. Here are the tasks:
There is a sequence of stones numbered 0,1,...,10^9 from left to right respectively. A chameleon is placed on the stone with number 0. There are N (1<=N<=10^5) flies on the other stones and more than one fly can share the same stone. To reach the i-th stone with his tongue, the chameleon loses i unities of energy. When he reach the i-th stone, he eats one of the flies on the stone. The flies on stones 1,2,...,i-1 moves one stone to the left, the flies on stones, i+1,... moves one stone to the right and the remaining flies on the i-th stone don't move. Given the number of flies N and their positions on the stones 1<=a1,a2,...,aN<=10^9, you are to find the minimum energy the chameleon will lose in order to eat all flies.
Given a dictionary of consisting of N (1<=N<=2000) words with length up to 20 lowercase letters and a string with up to 100 lowercase letters. It's known that the string is a sentence consisting of words from the dictionary written without spaces, you are to find the minimum number of words we need to use in a sentence so that writing it without spaces results in the given string. You need to print the actual sentence. If there are multiple solutions, print the one where the first word have minimum length. If there are still multiple solutions, print the one where the second word have the minimum length and so on and so on.
Just a short description of it. You need to write a compiler for a programming language called "EASY". The language uses 10 variables R0,R1,...,R9 and integer numbers from 0 to 999 inclusively. R0 is the value that the main function is called with and R9 contains the returning value. There are operations like MOV, ADD, SUB, MUL, DIV, MOD that you need to implement with the given variables or integer numbers from 0 to 999 inclusively. There are operators IFEQ(if equal), IFNEQ(if not equal), IFG(if greater), IFL(if less), IFGE(if greater or equal), IFLE(if less or equal) and an ENDIF operator for each of them. There are operators CALL and RET. CALL calls the main function recursively with a new value and RET returns a value. All R0,...,R8 are local, only R9 isn't since it stores the answer(the returned value). So it is all about coding and having strong nerves.
In this task you are given a string. You can mark a prefix of it and then by clicking a button your mark moves to the next occurence of the marked substring that does not overlap the current marked part. If there is no such an occurence, the mark stays at its place.
Some examples:
1 2312312312 -------> 123 1 2312312
12 312312312 -------> 123 12 312312
123 12312312 -------> 123 123 12312
1231 2312312 -------> 123123 1231 2
12312 312312 -------> 123123 12312
123123 12312 -------> 123123 12312
Your task is to find the length and the starting position of the longest substring such that after pressing that button the marked part to move.
In 15% of the tests 0 < n < 1000
In 25% of the tests 999 < n < 10000
In 60% of the tests 9999 < n < 1000000
Where n is the length of the string.
You are given a numeric system in base N where the first digits are: 1, 2, 3, ... N. Let them be c1, c2, c3, ... cN. You can write only 2-digit numbers. The task is to find the number of strictly increasing sequences in witch every digit is written twice and every number's first digit is less than its second. For example if N = 3 there is only 1 sequences of this type: c1c2, c1c3, c2,c3. Find the answer modulo 987654321.
You are given a matrix NxM. You need to delete all elements in the table. You can delete any side of the matrix. This operation will cost you the maximum number in the row/column. You need to find the minimum cost to delete the matrix. Example:
Input:
3 4
6 8 7 2
3 0 9 1
4 2 9 1
Output:
24
Explanation: One way you can delete the matrix for minimal cost: up, right, right, left, down
8 + 1 + 9 + 4 + 2 = 24
| Название |
|---|


