On every submission I get Ooops! Something has broken down in Codeforces page. Example problem that I've tried. Even if I submit solutions to problems that I've already solved before. I've tried multiple browsers: Brave, Chromium, Firefox. At the same time I see some other people having their problems judged.
cc: MikeMirzayanov
P.S. I couldn't find bug report option, so had to write a blog for that.
UPD: The issue is resolved shortly after posting this blog.









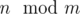 компонент размера
компонент размера 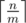 и
и 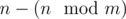 компонент размера
компонент размера 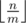 . Аналогично, для того, чтобы максимизировать количество ребер, на каждом шаге необходимо добавлять очередную вершину в компонентну связности наибольшего размера. Если действовать согласно такой стратегии, то образуется одна компонента связности размера
. Аналогично, для того, чтобы максимизировать количество ребер, на каждом шаге необходимо добавлять очередную вершину в компонентну связности наибольшего размера. Если действовать согласно такой стратегии, то образуется одна компонента связности размера 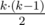 . Следует помнить про необходимость использовать 64-битный тип данных для хранения количества ребер, которое квадратично зависит от значения
. Следует помнить про необходимость использовать 64-битный тип данных для хранения количества ребер, которое квадратично зависит от значения 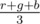 . Мы всегда можем украсить столько столов тремя воздушными шарами разных цветов. Очевидно, что оставшееся количество шаров будет меньше трех и, следовательно, не может быть использовано для украшения стола в любом случае. Все оставшиеся случаи имеет смысл свести к ранее рассмотренному. Если есть один цвет такой, что количество шариков этого цвета больше, чем суммарное количество шариков для оставшихся двух цветов, то всега выгодно украшать стол двумя шарами этого цвета и одним шаром того из оставшихся цветов, которого больше на данный момент. Далее можно разными способами группировать операции и выполнять более одной операции за раз. Другим решением можно назвать тот факт, что ответ будет отличен от
. Мы всегда можем украсить столько столов тремя воздушными шарами разных цветов. Очевидно, что оставшееся количество шаров будет меньше трех и, следовательно, не может быть использовано для украшения стола в любом случае. Все оставшиеся случаи имеет смысл свести к ранее рассмотренному. Если есть один цвет такой, что количество шариков этого цвета больше, чем суммарное количество шариков для оставшихся двух цветов, то всега выгодно украшать стол двумя шарами этого цвета и одним шаром того из оставшихся цветов, которого больше на данный момент. Далее можно разными способами группировать операции и выполнять более одной операции за раз. Другим решением можно назвать тот факт, что ответ будет отличен от 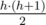 кубиков. Следовательно, высота полученной башни для заданных ограничений никогда не превысит
кубиков. Следовательно, высота полученной башни для заданных ограничений никогда не превысит 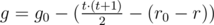 , где
, где 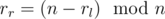 .
.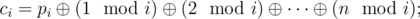
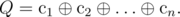
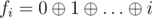 . Посчитаем значение этой функции для всех значений
. Посчитаем значение этой функции для всех значений 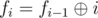 .
.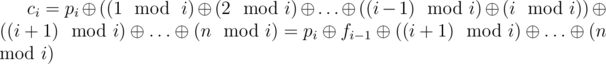
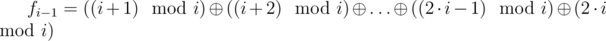

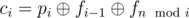 , иначе —
, иначе —  .
. 

 , где
, где