There are $$$m$$$ positive integers that add up to $$$n$$$. On each step take any two numbers, add the minimum of the two to the result and replace those two numbers with their sum (the size of the number set decreases by one). Repeat that until there is only one number left. Why is the result at most $$$n \log_2 n$$$? I have proof below which I don't know is correct or not. But I want to understand the intuition behind this one. Is there somewhere where I could read about this?

My idea is to use induction and see for myself that for small $$$n$$$ this works. Look at the last merge, we will have $$$n_1$$$ and $$$n_2$$$ such that $$$n_1+n_2=n$$$ and $$$n_1 \leq n_2$$$. By induction, the result by now is at most $$$n_1 \log n_1 + n_2 \log n_2$$$. We want to prove that $$$n_1 \log n_1 + n_2 \log n_2 + n_1 \leq n \log n$$$. To see that we can define $$$k = \frac{n_1}{n} \leq \frac 1 2$$$. We now want to prove:

But we know that $$$k \leq \frac 1 2$$$ meaning $$$\log k \leq -1$$$ and hence $$$1 + \log k \leq 0$$$ and now it's clear that both summands in the last line are at most 0.

Given n ≤ 10⁶ points with integer coordinates on a 2D plane, for each point compute the number of points with coordinates greater than those of the current one.

I can only think of a solution in which sorts the points using x coordinate, and then for every point count the number of points after it with greater y coordinate. That can be done by using Fenwick tree or segment tree.

Can we do better than that? Can we do something simpler without using a segment tree or Fenwick tree?

The other day in COCI Round #3 I didn't solve the problem Zoltan. Turns out the problem involved counting the # of LIS (longest increasing subsequence) in an array. I never coded this before and wanted to ask Codeforces community to verify that what I do is correct.

My idea is the following:

FindNumberOfLIS(nums):
    len is an array where len[i] is the length of LIS that ends at nums[i]
    cnt is an array where cnt[i] is the number of such LIS that end at nums[i]
    for i in [1..n]:
        let maxlen be the maximum len[j] for j in [1..i-1] and nums[j] < nums[i]
        let sumcnt be the sum of cnt[j] for j in [1..i-1] and nums[j] < nums[i] and len[j] == maxlen
        then len[i] is clearly maxlen+1 and cnt[i] = sumcnt
    return cnt[j] associated with maximum len[j]

The algorithm above is O(n²). If not for the constraint nums[j] < nums[i] we could have used segment tree. Therefore what I do is sort the initial nums into sortednums and create a segment tree relative to sortednums. Now on each step I would find maxlen and sumcnt in my segment tree from 1 to position of nums[i] in sortednums. In the end I return the sumcnt on the entire segment tree.

Can anyone tell me if it's correct? And if possible, tell me how you deal with duplicates since they are pretty annoying.

Given a rectangle on 2D plane ((0, 0), (a, b)) where 2 ≤ a, b ≤ 1000, two different points of me and another person (x₁, y₁) ≠ (x₂, y₂) such that x₁, y₁, x₂, y₂ are integers, 0 < x₁, x₂ < a, 0 < y₁, y₂ < b, and d — the range of our gun where 2 ≤ d ≤ 10000, find how many angles we can shoot at so that the bullet hits the other person and traveled at most a distance d.

When the bullet hits the wall it geometrically reflects against it, and if it hits the corner it bounces back.

Shooting another person means that the first person the bullet hits is the other person and not me, and the distance traveled by the bullet is at most d.

Sample: (a, b) = (3, 2), my position = (1, 1), other guy's position = (2, 1), d = 4

The answer is 7.

My solution right now is kind of reflect all the points over each of the walls, then do it over and over. Due to the constraints, it enough to reflect the points in each direction 5000 times. So in total, for directions it would give me somewhat around (2·5000)²·2 = 2·10⁸ points. Afterward, I sort the points by the angle relative to (x₁, y₁) and just go in that order, making sure the distance between me and the point of interest is at most d and that there are no other points between us (that's what I sorted).

Now this is slow since there are many points, I just thought maybe there are some other solutions?

I recently decided to work with Python 3 and I have questions regarding queues. As far as I understand the queue in the queue library is adapted for multithreaded programs. I assume that that queue is not as efficient as the simple queue (if I am wrong please correct). Therefore, I found that there is a deque from collections library which resembles deque in C++. Am I right that that's what competitive Python programmers use (for example, BFS problems)?

I want to find a problem like this:
Given a string s and array a of words, split s using words from a so that the least characters were left without matching to any of words.
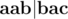So given s = 'aabbac' and a = {'aabb', 'c', 'aab', 'bac'} I expect s to be splited into not into 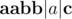because the last option gives me an extra character.
I am quite sure there is a problem like this somewhere in the web, but can anyone give me a link to it?
Thanks.