Note: This is NOT an official proof of the derived solution, as it is incoherent. It's rather a personal note for my illogical brain. It contains a derivation to the solution and the solution of Educational Codeforces Round 87 C2 at the bottom.
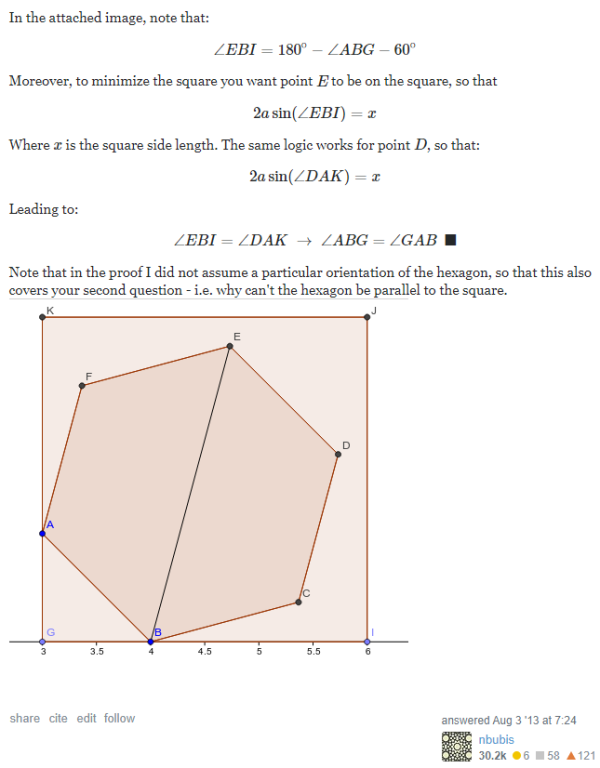
Source: https://math.stackexchange.com/a/458593/496530
From the above observation, 4 points of the polygon must be on the 4 sides of the minimal square. Each of 2 pairs, whose 2 points are on the opposite sides of the square, has the center of the polygon as its midpoint.
Below figures illustrate the minimal square when $$$n=5$$$. Half square on the left, full square on the right.
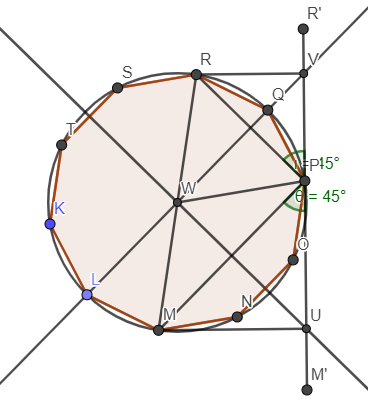
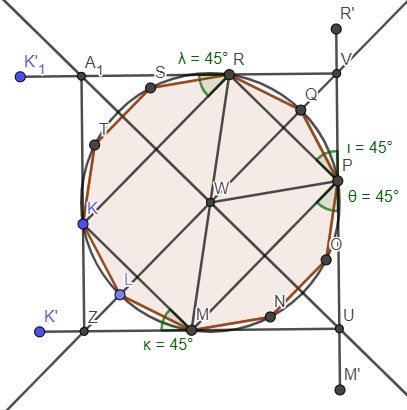
Consider the point of interest to be $$$P$$$. Let's say $$$P$$$ is $$$k$$$ sides away from R, and $$$n-k$$$ sides away from M measured along the polygon circumference, where $$$k\in [0;n]$$$. Consider the left figure, $$$WU$$$ is the perpendicular bisector of $$$MP$$$, $$$WV$$$ is the perpendicular bisector of $$$RP$$$. Select $$$U$$$ where $$$\measuredangle{MPU}=45^{\circ}$$$. Select $$$V$$$ where $$$\measuredangle{RPV}=45^{\circ}$$$.
Recall that $$$n$$$ is odd, when $$$k=\lfloor\frac{n}{2}\rfloor+1$$$, $$$VU$$$ is the side of the minimal square containing the polygon.
Let $$$d=RM$$$ be the diagonal of the polygon.
But, $$$|VU|=d*\sin(\measuredangle{RMU})$$$, $$$|VU|$$$ should be smaller with smaller $$$\measuredangle{RMU}$$$ by using $$$k+1,k+2,..,n$$$. Why do these fail?
Because, when $$$k>\lfloor\frac{n}{2}\rfloor+1$$$, from the way the square was built, some points are outside of the square.
We can visualize these failed cases by considering 1 of them in the figure below where $$$n=9$$$, $$$k=6$$$ i.e. $$$k>\lfloor\frac{n}{2}\rfloor+1$$$:
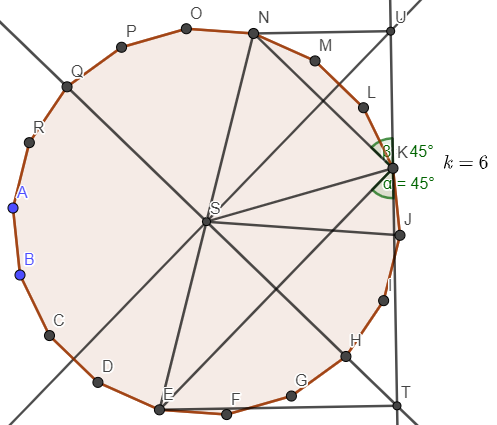
We can show that the point immediately below the chosen point ($$$K$$$) is out of the square by proving $$$\measuredangle{EKJ}>45^{\circ}$$$.
Proof:
Recall that $$$K$$$ is $$$k$$$ sides away from $$$E$$$ along the polygon circumference. In failed cases, $$$k>\lfloor\frac{n}{2}\rfloor+1$$$.
$$$\measuredangle{SKE}=90^{\circ}-\frac{1}{2}.\frac{180^{\circ}.k}{n}$$$
$$$\measuredangle{EKJ}=(180^{\circ}-\frac{180^{\circ}}{n}).\frac{1}{2}-\angle{SKE}=\frac{90^{\circ}}{n}.(k-1)$$$
From $$$k>\lfloor\frac{n}{2}\rfloor+1$$$, since $$$n$$$ is odd and $$$k$$$ is integer, therefore $$$k-1>\frac{n}{2}$$$, so:
$$$\measuredangle{EKJ}>\frac{90^{\circ}}{n}.\frac{n}{2}=45^{\circ} \blacksquare$$$
Therefore $$$J$$$ (hence $$$F$$$) will be outside of the bounding square.
Now for the satisfied $$$k$$$:
$$$k=\lfloor\frac{n}{2}\rfloor+1\implies\measuredangle{EKJ}=\frac{90^{\circ}}{n}.\lfloor\frac{n}{2}\rfloor<\frac{90^{\circ}}{n}.\frac{n}{2}=45^{\circ}$$$
This guarantees $$$J$$$ (hence $$$F$$$ and other points in between) will be inside of the bounding square.
End of reasoning.
Begin of derivation:
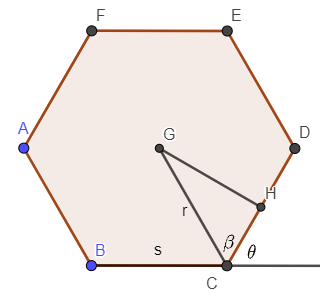
Let:
$$$r$$$ be the radius of the circumscribed circle of the polygon
$$$s$$$ be the length of the polygon side
$$$\beta$$$ be the angle formed by a radius and a polygon side
$$$\theta$$$ be the exterior angle of the polygon
$$$m$$$ be the number of sides of the polygon
$$$v$$$, $$$u$$$ be the length of the upper and lower segment of the side of the minimal square, separated by the chosen vertex ($$$k$$$ polygon sides away from the top intersection of polygon & minimal square, in second figure: $$$v=PV$$$, $$$u=PU$$$)
$$$k=\lfloor\frac{n}{2}\rfloor$$$ which is symmetrical to $$$k=\lfloor\frac{n}{2}\rfloor+1$$$ in the polygon
$$$\theta=\frac{360^{\circ}}{m}=\frac{360^{\circ}}{2n}$$$
$$$r.\cos{\beta}=\frac{s}{2}{\implies}r=\frac{s}{2\cos{\beta}}=\frac{s}{2\cos{(\frac{\pi}{2}-\frac{\theta}{2})}}=\frac{s}{2\sin{\frac{\theta}{2}}}$$$
$$$v=r.\sin{(\frac{1}{2}.\frac{{\pi}k}{n})}.\sqrt{2}=r\sqrt{2}\sin{(\frac{\pi}{2n}\lfloor\frac{n}{2}\rfloor)}$$$
$$$u=r.\sin{(\frac{1}{2}.\frac{\pi(n-k)}{n})}.\sqrt{2}=r\sqrt{2}\sin{(\frac{\pi}{2n}(n-\lfloor\frac{n}{2}\rfloor))}$$$
$$$ans=v+u$$$
For Educational Codeforces Round 87 C2:
double r = 1.0/(2.0*sin(PI/(2*n)));
double v = r*sin(PI/(2*n)*(n/2))*sqrt(2);
double u = r*sin(PI/(2*n)*(n-n/2))*sqrt(2);
double ans = v + u;
Recall that $$$n$$$ is odd, so $$$\lfloor\frac{n}{2}\rfloor=\frac{n-1}{2}$$$. We can further simplify $$$v+u$$$:
$$$v=r\sqrt{2}\sin{(\frac{\pi}{2n}.\frac{n-1}{2})}$$$
$$$u=r\sqrt{2}\sin{(\frac{\pi}{2n}.(n-\frac{n-1}{2}))}$$$
$$$ans=v+u=r\sqrt{2}[\sin{(\frac{\pi}{4}-\frac{\pi}{4n})}+\sin{(\frac{\pi}{4}+\frac{\pi}{4n})}]=\frac{\sqrt{2}}{2\sin{\frac{\theta}{2}}}.2\sin{\frac{\pi}{4}}\cos{\frac{-\pi}{4n}}$$$
$$$\implies ans=\frac{s.\cos{\frac{\pi}{4n}}}{\sin{\frac{\pi}{2n}}}$$$
So another solution to 1354C2 is:
double ans = cos(PI/(4*n))/(sin(PI/(2*n)));
All figures above (except the 1st figure) were drawn in GeoGebra Geometry. Additionally, GeoGebra is a a free dynamic mathematics software containing several apps:
Graphing calculator
Geometry
3D Calculator
CAS Calculator
Scientific Calculator










