Problem Link: https://atcoder.jp/contests/dwacon6th-final/tasks/dwacon6th_final_c
Statement
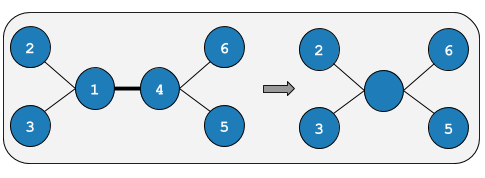
Given a tree with $$$n$$$ nodes, edge $$$i$$$ connects node $$$(u_i,v_i)$$$. For a permutation $$$p_1,p_2,\ldots,p_{n-1}$$$, the cost of it is defined as follows:
- For each $$$i$$$ from $$$1$$$ to $$$n-1$$$, in this order, do the following:
- Let $$$U = u_{p_i},V = v_{p_i}$$$ and $$$x = \text{degree}_U,y = \text{degree}_V$$$, get $$$x \cdot y$$$ points and delete this edge, then merge node $$$U,V$$$ into one node.
- The cost of permutation $$$p$$$ is the sum of points you get.
Count the total cost of all $$$(n-1)!$$$ permutations, modulo $$$998244353$$$.
UPD: I read the some AC code and find that the answer is $$$(n-1)! \cdot (a_1 + a_2 + \sum \limits_{i=3}^n \dfrac{4a_i}{i(i-1)})$$$, where $$$a_i$$$ is the number of paths of length $$$i$$$. But I still can't understand it :(