Introduction to Disjoint Set Data Strucutres
Hello Codeforces!
I recently read about Disjoint Sets from the book Introduction to Algorithms and wanted to share the learnings in a simplified manner.
So below article(and corresponding videos) is an attempt to create a good starting point for people who:
- want to learn about DSU
- practice some good DSU problems
Contents
- Introduction through an illustrative problem (video version: https://youtu.be/JDycPHW4kIs?si=WEp5Ft2jBWp9KnO2)
- Sample SPOJ Problem and Implementation (video version: https://youtu.be/O4w-aX5mSks?si=vr0XSbyUswcXx-Yv)
- Upcoming Practice Problems
- Some Applications and References
We will learn about disjoint set data structures and their operations union and find through a sample problem.
Illustrative Problem
Q: Given a undirected $$$Graph(V, E)$$$, answer Q queries of the form $$$(u, v)$$$ where answer to the query is True if there is a path from u to v, false otherwise. 
So for above graph:
- $$$query(D,A)$$$ = true
- $$$query(D,C)$$$ = true
- $$$query(D,F)$$$ = false
Some solutions to above problem
Solution1:
- For each query $$$(u, v)$$$, perform a BFS/DFS.
- Time Complexity will be $$$O(Q*(V + E))$$$
- In worst case graph can have order of $$$V^2$$$ Edges.
- So worst case complexity can be $$$O(Q*V^2)$$$
Solution2:
- perform 1 BFS/DFS per node of the Graph
- When BFS is done using node X, store all the nodes that can be visited from X.
- Per Query time is $$$O(1)$$$ so overall $$$O(Q)$$$
- Preprocessing time is $$$O(V * (V + E)) = O(V^3)$$$
- Hence overall $$$O(Q + V^3)$$$
What is a Disjoint Set Data Structure?
- It is a collection of disjoint dynamic sets. $$$D = {S1, S2, S3, …………, Sk}$$$
- Each set has a Representative R and consists of some elements.
- Assume total elements is N: $$$Size(S1) + Size(S2) + … + Size(Sk) = N$$$
A disjoint set structure supports:
- $$$MAKE-SET(X):$$$ Creates a new Set with only element X and representative X.
- $$$FIND(X):$$$ Returns the representative of the set to which X belongs.
- $$$UNION(X, Y):$$$ Unites the sets containing the elements X and Y into a single new Set. The representative of this set is usually either the representative of Sx or representative of Sy
Diagramatic Example of a disjoint set with total 8 elements and 3 sets:
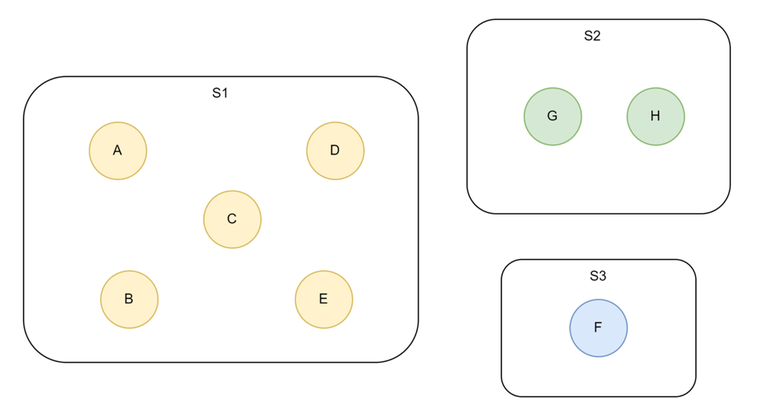
From above:
- $$$Find(H) = G$$$
- $$$Find(F) = F$$$
- $$$Find(B) =Find(E) = A$$$
[Assume that A, G and F are representative elements their sets]
Using Disjoint Set DS for solving the problem
- Run $$$MAKE-SET(u)$$$ for each of the V nodes in the graph.
- Run $$$UNION(u,v)$$$ for each edge $$$(u,v)$$$ in the graph.
- For each Query (u,v): a) If $$$FIND(u) == FIND(v)$$$ then answer = true b) Else answer = false
Running 1. and 2. on sample graph constructs the Disjoint set data structure shown in diagram.
Time complexity for DSU solution
Overall Complexity is sum of:
- $$$O(V * MAKE-SET)$$$
- $$$O(E * UNION) = O(V^2 * UNION)$$$
- $$$O(Q * FIND)$$$
Disjoint Set — Linked List Implementation
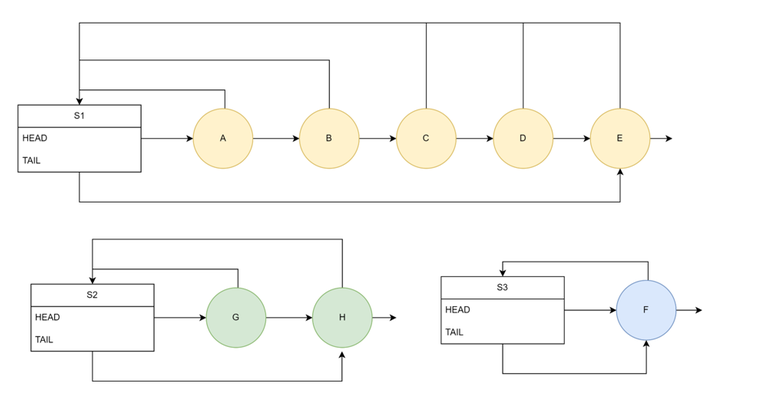
- Each set is represented as a link list.
- The set has HEAD pointer to representative element and also a TAIL pointer.
- Each element of the set has a back-pointer to the set.
Complexity Analysis for link list implementation
- Make Set is O(1) -> only need to create a new set with 1 element
- Find Set is O(1) -> thanks to back pointers
- Union is length of the longer set -> no-thanks to back pointers(all of 2nd set element back-pointers need to be updated to 1st set)
Note: For a total of N elements in the collection there will be at most N-1 union operations as post that all elements will be in the same set.
Worst Case cost of Union is when:
- All sets have size 1.
- 1st union we unite two sets of size 1 and get a set of size 2 -> cost is 1 back pointer change.
- 2nd time we unite a set of size 1 with a set of size 2 -> cost is 2 back pointer change.
- ith time we unite a set of size 1 with a set of size i -> cost is i back pointer change.
- Overall cost over n-1 union operations is $$$1 + 2 + 3 + .. + n-1 = O(N^2)$$$
Hence union is still $$$O(N)$$$ in the worst case.
Weighted Union Heuristic for link list Implementation
While performing $$$union(x,y)$$$:
- Always take smaller set and attach it the larger set.
- Need to maintain size of set for each set(which should be easy)
Complexity analysis: Union is now $$$O(logN)$$$, but why?
- The cost of a union operation is the cost of changing back pointers of the elements in the smaller set.
- Say we change the back pointer of an Element X belonging to $$$S_x$$$, the resulting set will have at least $$$2 * S_x$$$ elements.(since X belong to smaller set and hence it's backpointer was updated)
- If back pointer of X is changed K times there need to be $$$>= (2^K) * S_x$$$ elements
- K can be at most log(N) as we only have N elements.
- hence for a given element we can change the back-pointer at most logN times and overall cost $$$<= NlogN$$$
Revisiting the sample problem
Worst Case complexity of Graph problem has now Improved :)
- $$$O(V * MAKE-SET) = O(V)$$$
- $$$O(E * UNION) = O(V^2 * UNION) = O(V^2 * logV) = O(V^2 * logV)$$$
- $$$O(Q * FIND) = O(Q)$$$
So $$$O(V^2 * logV)$$$ instead of $$$O(V^3)$$$
Disjoint Set — Forest Implementation
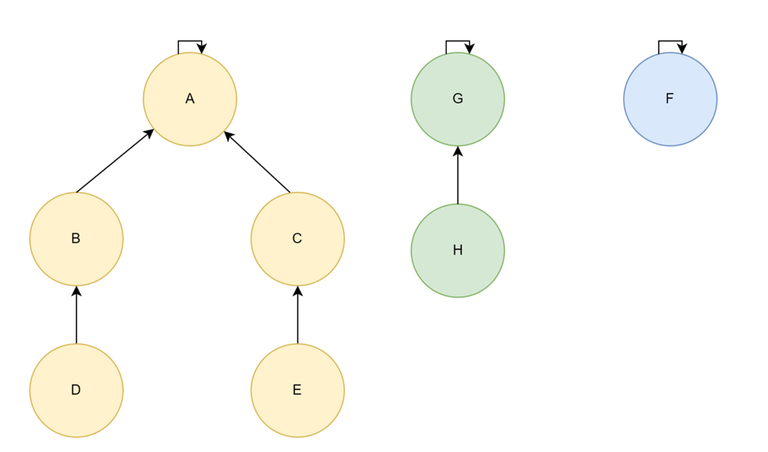
- Each set is represented as a tree.
- Each element is a node of the tree and maintains a pointer to it's parent in the tree.
- The representative element is the parent of itself.
$$$Find(X) = X \;if\,parent[X] = X \;else\,Find(X) = Find(parent[X])$$$
Forest Implementation — Time Complexities
We may still end up getting a chain :(
Worst case complexities:
- UNION is $$$O(1) * O(FIND)$$$ in worst case(only need to change parent pointer of one representative to another, problem is finding the representative using FIND)
- MAKE SET is $$$O(1)$$$ in worst case(only need to create a set with 1 element which is it's own parent)
- FIND however is $$$O(N)$$$ in the worst case(we may end up getting a link list)
Time Complexities with Heuristics
Heuristic: Union by Rank
While performing union always take the Set(tree) with less height and attach it to the set with greater height.
- Overall height after N-1 union will be order of LogN
- Hence ensuring Find is no worse than LogN
Heuristic: Path Compression When performing find operation, change the parent pointer of each node to the actual representative of the node. 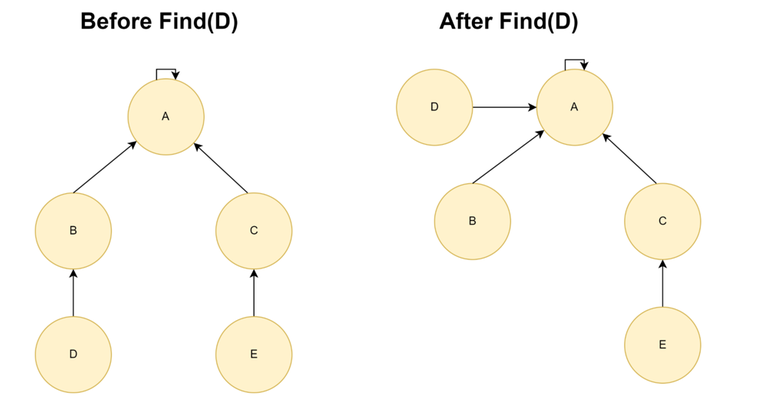
The time complexity when applying both heuristics together is:
- Make Set is $$$O(1)$$$
- Find Set is $$$O(\alpha(n))$$$
- Union is amortised $$$O(\alpha(n))$$$
What is $$$\alpha(n)$$$?
- Where alpha is the inverse of Ackerman function $$$A_k(1)$$$
- $$$\alpha(n) <= 4$$$ for all $$$N <= 16^{512}$$$
- $$$16^{512}\; »\; 10^{80}$$$
- $$$10^80$$$ is the number of atoms in observable universe
Hence for all practical purposes $$$\alpha(n) = 4 = constant$$$.
Proof is harder and omitted from scope of this article, refer Introduction To Algorithms by Thomas H. Cormen
Revisiting the sample problem
- Make Set is $$$O(1)$$$
- Find Set is $$$O(1)$$$
- Union is $$$amortised O(\alpha(n))$$$
Worst Case complexity of Graph problem has now Improved :)
- $$$O(V * MAKE-SET) = O(V)$$$
- $$$O(E * UNION) = O(V^2 * UNION) = O(V^2 * logV) = O(V^2 * \alpha(V))$$$
- $$$O(Q * FIND) = O(Q)$$$
Hence time complexity is now $$$O(V^2 + Q)$$$ for all practical purposes.
SPOJ Problem — FRNDCIRC + Generic Implementation
- Problem Link: https://www.spoj.com/problems/FRNDCIRC/
- Solution link: https://youtu.be/O4w-aX5mSks?si=UQJwpjayddjVK5uw
- Code implementation: https://ideone.com/Bdh2It
Upcoming Practice Problems
Currently I have planned the problem https://codeforces.me/problemset/problem/150/B and will be soon adding both a written and video editorial for the same.
Few other practice problems include: https://codeforces.me/blog/entry/55219?#comment-390897 (DSU tag). I will be using some of these to create more editorials.
If you have more suggestions please add in comments.
Applications and References
Some direct applications:
- Finding cycles in a graph
- Kruskals minimum spanning tree algorithm
Some references:
- https://www.youtube.com/@AlgosWithKartik
- Introduction to Algorithms Book
- CP algorithms: https://cp-algorithms.com/data_structures/disjoint_set_union.html











