Hope you enjoyed the problems!
UPD 1: Added implementations!
UPD 2: It seems my wording for the solution to C is not the best, and it is causing some confusion. I've updated it to be better!
UPD 3: Implementation links didn't work for some reason, so I've just added the code directly.
Look at the distance between the frogs.
Notice that regardless of how the players move, the difference between the numbers of the lilypads the two players are standing on always alternates even and odd, depending on the starting configuration. Then, the key observation is that exactly one player has the following winning strategy:
- Walk towards the other player, and do not stop until they are forced onto lilypad $$$1$$$ or $$$n$$$.
For instance, if Alice and Bob start on lilypads with the same parity, Bob cannot stop Alice from advancing towards him. This is because at the start of Alice's turn, she will always be able to move towards Bob due to their distance being even and therefore at least $$$2$$$, implying that there is a free lilypad for her to jump to. This eventually forces Bob into one of the lilypads $$$1, n$$$, causing him to lose.
In the case that they start on lilypads with different parity, analogous logic shows that Bob wins. Therefore, for each case, we only need to check the parity of the lilypads for a constant time solution.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int T; cin >> T;
while (T--) {
int N, A, B; cin >> N >> A >> B;
if ((A ^ B) & 1) cout << "NO\n";
else cout << "YES\n";
}
cout.flush();
return 0;
}
The order of the moves is pretty much irrelevant. What happens if we try to make two different materials?
The key observation is that we will never use the operation to craft two different types of materials $$$i, j$$$. This is because if we were to combine the net change in resources from these two operations, we would lose two units each of every material $$$k \neq i, j$$$, and receive a net zero change in our amounts of materials $$$i, j$$$. Therefore, we will only ever use the operation on one type of material $$$i$$$.
An immediate corollary of this observation is that we can only be deficient in at most one type of material, i.e. at most one index $$$i$$$ at which $$$a_i < b_i$$$. If no such index exists, the material is craftable using our starting resources. Otherwise, applying the operation $$$x$$$ times transforms our array to
i.e. increasing element $$$a_i$$$ by $$$x$$$ and decreasing all other elements by $$$x$$$. We must have $$$x \geq b_i - a_i$$$ to satisfy the requirement on material type $$$i$$$. However, there is also no point in making $$$x$$$ any larger, as by then we already have enough of type $$$i$$$, and further operations cause us to start losing materials from other types that we could potentially need to craft the artifact. Therefore, our condition in this case is just to check that
i.e. we are deficient in type $$$i$$$ by at most as many units as our smallest surplus in all other material types $$$j \neq i$$$. This gives an $$$O(n)$$$ solution.
// #include <ext/pb_ds/assoc_container.hpp>
// #include <ext/pb_ds/tree_policy.hpp>
// using namespace __gnu_pbds;
// typedef tree<int, null_type, std::less<int>, rb_tree_tag, tree_order_statistics_node_update> ordered_set;
#include <bits/stdc++.h>
#define f first
#define s second
#define pb push_back
typedef long long int ll;
typedef unsigned long long int ull;
using namespace std;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
template<typename T> int die(T x) { cout << x << endl; return 0; }
#define mod_fft 998244353
#define mod_nfft 1000000007
#define INF 100000000000000
#define LNF 1e15
#define LOL 12345678912345719ll
struct LL {
static const ll m = mod_fft;
long long int val;
LL(ll v) {val=reduce(v);};
LL() {val=0;};
~LL(){};
LL(const LL& l) {val=l.val;};
LL& operator=(int l) {val=l; return *this;}
LL& operator=(ll l) {val=l; return *this;}
LL& operator=(LL l) {val=l.val; return *this;}
static long long int reduce(ll x, ll md = m) {
x %= md;
while (x >= md) x-=md;
while (x < 0) x+=md;
return x;
}
bool operator<(const LL& b) { return val<b.val; }
bool operator<=(const LL& b) { return val<=b.val; }
bool operator==(const LL& b) { return val==b.val; }
bool operator>=(const LL& b) { return val>=b.val; }
bool operator>(const LL& b) { return val>b.val; }
LL operator+(const LL& b) { return LL(val+b.val); }
LL operator+(const ll& b) { return (*this+LL(b)); }
LL& operator+=(const LL& b) { return (*this=*this+b); }
LL& operator+=(const ll& b) { return (*this=*this+b); }
LL operator-(const LL& b) { return LL(val-b.val); }
LL operator-(const ll& b) { return (*this-LL(b)); }
LL& operator-=(const LL& b) { return (*this=*this-b); }
LL& operator-=(const ll& b) { return (*this=*this-b); }
LL operator*(const LL& b) { return LL(val*b.val); }
LL operator*(const ll& b) { return (*this*LL(b)); }
LL& operator*=(const LL& b) { return (*this=*this*b); }
LL& operator*=(const ll& b) { return (*this=*this*b); }
static LL exp(const LL& x, const ll& y){
ll z = y;
z = reduce(z,m-1);
LL ret = 1;
LL w = x;
while (z) {
if (z&1) ret *= w;
z >>= 1; w *= w;
}
return ret;
}
LL& operator^=(ll y) { return (*this=LL(val^y)); }
LL operator/(const LL& b) { return ((*this)*exp(b,-1)); }
LL operator/(const ll& b) { return (*this/LL(b)); }
LL operator/=(const LL& b) { return ((*this)*=exp(b,-1)); }
LL& operator/=(const ll& b) { return (*this=*this/LL(b)); }
}; ostream& operator<<(ostream& os, const LL& obj) { return os << obj.val; }
int N;
vector<ll> segtree;
void pull(int t) {
segtree[t] = max(segtree[2*t], segtree[2*t+1]);
}
void point_set(int idx, ll val, int L = 1, int R = N, int t = 1) {
if (L == R) segtree[t] = val;
else {
int M = (L + R) / 2;
if (idx <= M) point_set(idx, val, L, M, 2*t);
else point_set(idx, val, M+1, R, 2*t+1);
pull(t);
}
}
ll range_add(int left, int right, int L = 1, int R = N, int t = 1) {
if (left <= L && R <= right) return segtree[t];
else {
int M = (L + R) / 2;
ll ret = 0;
if (left <= M) ret = max(ret, range_add(left, right, L, M, 2*t));
if (right > M) ret = max(ret, range_add(left, right, M+1, R, 2*t+1));
return ret;
}
}
void build(vector<ll>& arr, int L = 1, int R = N, int t = 1) {
if (L == R) segtree[t] = arr[L-1];
else {
int M = (L + R) / 2;
build(arr, L, M, 2*t);
build(arr, M+1, R, 2*t+1);
pull(t);
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
int T = 1; cin >> T;
while (T--) {
int N; cin >> N;
vector<int> A(N), B(N);
for (int i = 0; i < N; i++) cin >> A[i];
int bad = -1, margin = 1e9, need = 0;
bool reject = 0;
for (int i = 0; i < N; i++) {
cin >> B[i];
if (A[i] < B[i]) {
if (bad != -1) reject = 1;
bad = i;
need = B[i] - A[i];
} else {
margin = min(margin, A[i] - B[i]);
}
}
if (reject) {
cout << "NO" << endl;
continue;
} else {
cout << ((margin >= need) ? "YES" : "NO") << endl;
}
}
}
Pick $$$x$$$, and find the sum of the whole grid. What does this tell you?
Once you know $$$x$$$, the top left cell is fixed.
What about the next cell on the trail?
The naive solution of writing out a linear system and solving them will take $$$O((n + m)^3)$$$ time, which is too slow, so we will need a faster algorithm.
We begin by selecting a target sum $$$S$$$ for each row and column. If we calculate the sum of all numbers in the completed grid, summing over rows gives a total of $$$S \cdot n$$$ while summing over columns gives a total of $$$S \cdot m$$$. Therefore, in order for our choice of $$$S$$$ to be possible, we require $$$S \cdot n = S \cdot m$$$, and since it is possible for $$$n \neq m$$$, we will pick $$$S = 0$$$ for our choice to be possible in all cases of $$$n, m$$$. Notice that all choices $$$S \neq 0$$$ will fail on $$$n \neq m$$$, as the condition $$$S \cdot n = S \cdot m$$$ no longer holds. As such, $$$S = 0$$$ is the only one that will work in all cases.
Now, we aim to make each row and column sum to $$$S$$$. The crux of the problem is the following observation:
- Denote $$$x_1, x_2, \dots, x_{n+m-1}$$$ to be the variables along the path. Let's say variables $$$x_1, \dots, x_{i-1}$$$ have their values set for some $$$1 \leq i < n+m-1$$$. Then, either the row or column corresponding to variable $$$x_i$$$ has all of its values set besides $$$x_i$$$, and therefore we may determine exactly one possible value of $$$x_i$$$ to make its row or column sum to $$$0$$$.
The proof of this claim is simple. At variable $$$x_i$$$, we look at the corresponding path move $$$s_i$$$. If $$$s_i = \tt{R}$$$, then the path will never revisit the column of variable $$$x_i$$$, and its column will have no remaining unset variables since $$$x_1, \dots, x_{i-1}$$$ are already set. Likewise, if $$$s_i = \tt{D}$$$, then the path will never revisit the row of variable $$$x_i$$$, which can then be used to determine the value of $$$x_i$$$.
Repeating this process will cause every row and column except for row $$$n$$$ and column $$$m$$$ to have a sum of zero, with $$$x_{n+m-1}$$$ being the final variable. However, we will show that we can use either the row or column to determine it, and it will give a sum of zero for both row $$$n$$$ and column $$$m$$$. WLOG we use row $$$n$$$. Indeed, if the sum of all rows and columns except for column $$$m$$$ are zero, we know that the sum of all entries of the grid is zero by summing over rows. However, we may then subtract all columns except column $$$m$$$ from this total to arrive at the conclusion that column $$$m$$$ also has zero sum. Therefore, we may determine the value of $$$x_{n+m-1}$$$ using either its row or column to finish our construction, giving a solution in $$$O(n \cdot m)$$$.
#include <bits/stdc++.h>
#define f first
#define s second
#define pb push_back
typedef long long int ll;
typedef unsigned long long int ull;
using namespace std;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
template<typename T> int die(T x) { cout << x << endl; return 0; }
#define mod 1000000007
#define INF 1000000000
#define LNF 1e15
#define LOL 12345678912345719ll
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int T; cin >> T;
while (T--) {
int N, M; cin >> N >> M;
string S; cin >> S;
vector<vector<ll>> A;
for (int i = 0; i < N; i++) {
A.push_back(vector<ll>(M));
for (int j = 0; j < M; j++) {
cin >> A[i][j];
}
}
int x = 0, y = 0;
for (char c : S) {
if (c == 'D') {
long long su = 0;
for (int i = 0; i < M; i++) {
su += A[x][i];
}
A[x][y] = -su;
++x;
} else {
long long su = 0;
for (int i = 0; i < N; i++) {
su += A[i][y];
}
A[x][y] = -su;
++y;
}
}
long long su = 0;
for (int i = 0; i < M; i++) {
su += A[N-1][i];
}
A[N-1][M-1] = -su;
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
cout << A[i][j] << " ";
}
cout << endl;
}
}
return 0;
}
Should you ever change the order of scarecrows?
What's the first thing that the leftmost scarecrow should do?
What's the only way to save time? Think in terms of distances and not times.
Look at the points where the crow "switches over" between scarecrows.
Greedy.
We make a few preliminary observations:
- (1) The order of scarecrows should never change, i.e no two scarecrows should cross each other while moving along the interval.
- (2) Scarecrow $$$1$$$ should spend the first $$$a_1$$$ seconds moving to position zero, as this move is required for the crow to make any progress and there is no point in delaying it.
- (3) Let's say that a scarecrow at position $$$p$$$ `has' the crow if the crow is at position $$$p + k$$$, and there are no other scarecrows in the interval $$$[p, p+k]$$$. A scarecrow that has the crow should always move to the right; in other words, all scarecrows that find themselves located to the left of the crow should spend all their remaining time moving to the right, as it is the only way they will be useful.
- (4) Let there be a scenario where at time $$$T$$$, scarecrow $$$i$$$ has the crow and is at position $$$x$$$, and another scenario at time $$$T$$$ where scarecrow $$$i$$$ also has the crow, but is at position $$$y \geq x$$$. Then, the latter scenario is at least as good as the former scenario, assuming scarecrows numbered higher than $$$i$$$ are not fixed.
- (5) The only way to save time is to maximize the distance $$$d$$$ teleported by the crow.
The second and fifth observations imply that the time spent to move the crow across the interval is $$$a_1 + \ell - d$$$.
Now, for each scarecrow $$$i$$$, define $$$b_i$$$ to be the position along the interval at which it begins to have the crow, i.e. the crow is transferred from scarecrow $$$i-1$$$ to $$$i$$$. For instance, in the second sample case the values of $$$b_i$$$ are
The second observation above implies that $$$b_1 = 0$$$, and the first observation implies that $$$b_1 \leq \dots \leq b_n$$$. Notice that we may express the distance teleported as
with the extra definition that $$$b_{n+1} = \ell$$$. For instance, in the second sample case the distance teleported is
and the total time is $$$a_1 + \ell - d = 2 + 5 - 4.5 = 2.5$$$.
Now, suppose that $$$b_1, \dots, b_{i-1}$$$ have been selected for some $$$2 \leq i \leq n$$$, and that time $$$T$$$ has elapsed upon scarecrow $$$i-1$$$ receiving the crow. We will argue the optimal choice of $$$b_i$$$.
At time $$$T$$$ when scarecrow $$$i-1$$$ first receives the crow, scarecrow $$$i$$$ may be at any position in the interval $$$[a_i - T, \min(a_i + T, \ell)]$$$. Now, we have three cases.
Case 1. $$$b_{i-1} + k \leq a_i - T.$$$ In this case, scarecrow $$$i$$$ will need to move some nonnegative amount to the left in order to meet with scarecrow $$$i-1$$$. They will meet at the midpoint of the crow position $$$b_{i-1} + k$$$ and the leftmost possible position $$$a_i - T$$$ of scarecrow $$$i$$$ at time $$$T$$$. This gives
Case 2. $$$a_i - T \leq b_{i-1} + k \leq a_i + T.$$$ Notice that if our choice of $$$b_i$$$ has $$$b_i < b_{i-1} + k$$$, it benefits us to increase our choice of $$$b_i$$$ (if possible) as a consequence of our fourth observation, since all such $$$b_i$$$ will cause an immediate transfer of the crow to scarecrow $$$i$$$ at time $$$T$$$. However, if we choose $$$b_i > b_{i-1} + k$$$, lowering our choice of $$$b_i$$$ is now better as it loses less potential teleported distance $$$\min(k, b_i - b_{i-1})$$$, while leaving more space for teleported distance after position $$$b_i$$$. Therefore, we will choose $$$b_i := b_{i-1} + k$$$ in this case.
Case 3. $$$a_i + T \leq b_{i-1} + k.$$$ In this case, regardless of how we choose $$$b_i$$$, the crow will immediately transfer to scarecrow $$$i$$$ from scarecrow $$$i-1$$$ at time $$$T$$$. We might as well pick $$$b_i := a_i + T$$$.
Therefore, the optimal selection of $$$b_i$$$ may be calculated iteratively as
It is now easy to implement the above approach to yield an $$$O(n)$$$ solution. Note that the constraints for $$$k, \ell$$$ were deliberately set to $$$10^8$$$ instead of $$$10^9$$$ to make two times the maximum answer $$$4 \cdot \ell$$$ fit within $$$32$$$-bit integer types. It is not difficult to show that the values of $$$b_i$$$ as well as the answer are always integers or half-integers.
#include <bits/stdc++.h>
#define f first
#define s second
#define pb push_back
typedef long long int ll;
typedef unsigned long long int ull;
using namespace std;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int T; cin >> T;
while (T--) {
int N, k, l;
cin >> N >> k >> l;
double K = k;
double L = l;
vector<int> A(N);
for (int i = 0; i < N; i++) cin >> A[i];
double T = A[0];
double last_pt = 0;
double S = 0;
for (int i = 1; i < N; i++) {
double this_pt = min(L, min(A[i] + T,
max(last_pt + K,
(A[i] - T + last_pt + K)/2.0)));
T += max(0.0, this_pt - last_pt - K);
S += min(K, this_pt - last_pt);
last_pt = this_pt;
}
S += min(K, L - last_pt);
cout << (int)round(2*(L - S + A[0])) << endl;
}
return 0;
}
Let's say you have to empty the haystacks in a fixed order. What's the best way to do it?
Write the expression for the number of moves for a given order.
In an optimal ordering, you should not gain anything by swapping two entries of the order. Using this, describe the optimal order.
The constraint only limits what you can empty last. How can you efficiently compute the expression in Hint 2?
Let's say we fixed some permutation $$$\sigma$$$ of $$$1, \dots, n$$$ such that we empty haystacks in the order $$$\sigma_1, \dots, \sigma_n$$$. Notice that a choice of $$$\sigma$$$ is possible if and only if the final stack $$$\sigma_n$$$ can be cleared, which is equivalent to the constraint
With this added constraint, the optimal sequence of moves is as follows:
- Iterate $$$i$$$ through $$$1, \dots, n-1$$$. For each $$$i$$$, try to move its haybales to haystacks $$$1, \dots, i-1$$$, and if they are all full then move haybales to haystack $$$n$$$. Once this process terminates, move all haystacks from $$$n$$$ back onto arbitrary haystacks $$$1, \dots, n-1$$$, being careful to not overflow the height limits.
The key observation is that the number of extra haybales that must be moved onto haystack $$$n$$$ is
To show this, consider the last time $$$i$$$ that a haybale is moved onto haystack $$$n$$$. At this time, all haybales from haystacks $$$1, \dots, i$$$ have found a home, either on the height limited haystacks $$$1, \dots, i-1$$$ or on haystack $$$n$$$, from which the identity immediately follows. Now, every haystack that wasn't moved onto haystack $$$n$$$ will get moved once, and every haystack that did gets moved twice. Therefore, our task becomes the following: Compute
for $$$\sigma$$$ satisfying
Notice that the $$$\sum_{i=1}^n a_i$$$ term is constant, and we will omit it for the rest of this tutorial. We will first solve the task with no restriction on $$$\sigma$$$ to gain some intuition. Denote $$$<_{\sigma}$$$ the ordering of pairs $$$(a, b)$$$ corresponding to $$$\sigma$$$.
Consider adjacent pairs $$$(a_i, b_i) <_{\sigma} (a_j, b_j)$$$. Then, if the choice of $$$\sigma$$$ is optimal, it must not be better to swap their ordering, i.e.
As a corollary, there exists an optimal $$$\sigma$$$ satisfying the following properties:
Claim [Optimality conditions of $\sigma$].
- All pairs with $$$a_i < b_i$$$ come first. Then, all pairs with $$$a_i = b_i$$$ come next. Then, all pairs with $$$a_i > b_i$$$.
- The pairs with $$$a_i < b_i$$$ are in ascending order of $$$a_i$$$.
- The pairs with $$$a_i > b_i$$$ are in descending order of $$$b_i$$$.
It is not hard to show that all such $$$\sigma$$$ satisfying these properties are optimal by following similar logic as above. We leave it as an exercise for the reader.
Now, we add in the constraint on the final term $$$\sigma_n$$$ of the ordering. We will perform casework on this final haystack. Notice that for any fixed $$$a_n, b_n$$$, if
is maximized, then so is
So, if we were to fix any last haystack $$$\sigma_n$$$, the optimality conditions tell us that we should still order the remaining $$$n-1$$$ haystacks as before. Now, we may iterate over all valid $$$\sigma_n$$$ and compute the answer efficiently as follows: maintain a segment tree with leaves representing pairs $$$(a_i, b_i)$$$ and range queries for
This gives an $$$O(n \log n)$$$ solution.
Note that it is possible to implement this final step using prefix and suffix sums to yield an $$$O(n)$$$ solution, but it is not necessary to do so.
#include <bits/stdc++.h>
#define f first
#define s second
#define pb push_back
typedef long long int ll;
typedef unsigned long long int ull;
using namespace std;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
template<typename T> int die(T x) { cout << x << endl; return 0; }
#define LNF 1e15
int N;
vector<pll> segtree;
pll f(pll a, pll b) {
return {max(a.first, a.second + b.first), a.second + b.second};
}
void pull(int t) {
segtree[t] = f(segtree[2*t], segtree[2*t+1]);
}
void point_set(int idx, pll val, int L = 1, int R = N, int t = 1) {
if (L == R) segtree[t] = val;
else {
int M = (L + R) / 2;
if (idx <= M) point_set(idx, val, L, M, 2*t);
else point_set(idx, val, M+1, R, 2*t+1);
pull(t);
}
}
pll range_add(int left, int right, int L = 1, int R = N, int t = 1) {
if (left <= L && R <= right) return segtree[t];
else {
int M = (L + R) / 2;
pll ret = {0, 0};
if (left <= M) ret = f(ret, range_add(left, right, L, M, 2*t));
if (right > M) ret = f(ret, range_add(left, right, M+1, R, 2*t+1));
return ret;
}
}
void build(vector<pll>& arr, int L = 1, int R = N, int t = 1) {
if (L == R) segtree[t] = arr[L-1];
else {
int M = (L + R) / 2;
build(arr, L, M, 2*t);
build(arr, M+1, R, 2*t+1);
pull(t);
}
}
vector<int> theoretical(const vector<pii>& arr) {
vector<int> idx(arr.size());
for (int i = 0; i < arr.size(); ++i) {
idx[i] = i;
}
vector<int> ut, eq, lt;
for (int i = 0; i < arr.size(); ++i) {
if (arr[i].first < arr[i].second) {
ut.push_back(i);
} else if (arr[i].first == arr[i].second) {
eq.push_back(i);
} else {
lt.push_back(i);
}
}
sort(ut.begin(), ut.end(), [&arr](int i, int j) {
return arr[i].first < arr[j].first;
});
sort(eq.begin(), eq.end(), [&arr](int i, int j) {
return arr[i].first > arr[j].first;
});
sort(lt.begin(), lt.end(), [&arr](int i, int j) {
return arr[i].second > arr[j].second;
});
vector<int> result;
result.insert(result.end(), ut.begin(), ut.end());
result.insert(result.end(), eq.begin(), eq.end());
result.insert(result.end(), lt.begin(), lt.end());
return result;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
int T = 1; cin >> T;
while (T--) {
cin >> N;
vector<pll> data(N);
ll sum_a = 0;
ll sum_b = 0;
for (int i = 0; i < N; i++) {
cin >> data[i].f >> data[i].s;
sum_a += data[i].f;
sum_b += data[i].s;
}
vector<int> order = theoretical(vector<pii>(data.begin(), data.end()));
vector<pll> data_sorted;
for (int i : order) data_sorted.push_back({data[i].first, data[i].first - data[i].second});
data_sorted.push_back({0, 0});
++N;
segtree = vector<pll>(4*N);
build(data_sorted);
ll ans = LNF;
for (int i = 0; i < N-1; i++) {
if (sum_b - (data_sorted[i].first - data_sorted[i].second) >= sum_a) {
point_set(i+1, data_sorted[N-1]);
point_set(N, data_sorted[i]);
ans = min(ans, range_add(1, N).first);
point_set(i+1, data_sorted[i]);
point_set(N, data_sorted[N-1]);
}
}
if (ans == LNF) cout << -1 << endl;
else cout << ans + sum_a << endl;
}
}
The results of the partition must be convex. Can you see why?
The easier cases are when the polyomino must be cut vertically or horizontally. Let's discard those for now, and consider the "diagonal cuts". I.e. let one polyomino start from the top row, and another starting from some row $$$c$$$. WLOG the one starting on row $$$c$$$ is on the left side, we will check the other side by just duplicating the rest of the solution.
Both sub-polyominoes are fixed if you choose $$$c$$$. But, it takes $$$O(n)$$$ time to check each one.
Can you get rid of most $$$c$$$ with a quick check?
Look at perimeters shapes, or area. Both will work.
Assume there exists a valid partition of the polyomino. Note that the resulting congruent polyominoes must be convex, as it is not possible to join two non-overlapping non-convex polyominoes to create a convex one.
Then, there are two cases: either the two resulting polyominoes are separated by a perfectly vertical or horizontal cut, or they share some rows. The first case is easy to check in linear time. The remainder of the solution will focus on the second case.
Consider the structure of a valid partition. We will focus on the perimeter: 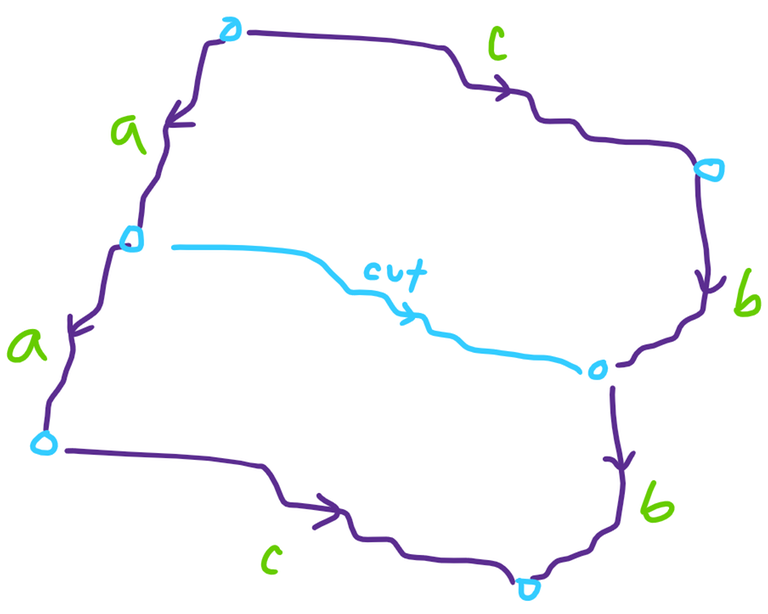
Notice that the cut separating the two polyominoes must only ever move down and right, or up and right, as otherwise one of the formed polyominoes will not be convex. Without loss of generality, say it only goes down and right.
In order for our cut to be valid, it must partition the perimeter into six segments as shown, such that the marked segments are congruent in the indicated orientations ($$$a$$$ with $$$a$$$, $$$b$$$ with $$$b$$$, $$$c$$$ with $$$c$$$.) If we label the horizontal lines of the grid to be $$$0, \dots, n$$$ where line $$$i$$$ is located after row $$$i$$$, we notice that the division points along the left side of the original polyomino are located at lines $$$0, k, 2k$$$ for some $$$1 \leq k \leq n/2$$$.
Notice that if we were to fix a given $$$k$$$, we can uniquely determine the lower polyomino from the first few rows of the upper polyomino. Indeed, if $$$a_i = r_i - \ell_i + 1$$$ denotes the width of the $$$i$$$-th row of the original polyomino, we can show that the resulting polyomino for a particular choice of $$$k$$$ has
cells in its $$$i$$$-th row, for $$$1 \leq i \leq n - k$$$. Therefore, iterating over all possible $$$k$$$ and checking them individually gives an $$$O(n^2)$$$ solution.
To speed this up, we will develop a constant-time check that will prune ``most'' choices of $$$k$$$. Indeed, we may use prefix sums and hashing to verify the perimeter properties outlined above, so that we can find all $$$k$$$ that pass this check in $$$O(n)$$$ time. If there are at most $$$f(n)$$$ choices of $$$k$$$ afterwards, we can check them all for a solution in $$$O(n \cdot (f(n) + \text{hashing errors}))$$$.
It can actually be shown that for our hashing protocol, $$$f(n) \leq 9$$$, so that this algorithm has linear time complexity. While the proof is not difficult, it is rather long and will be left as an exercise. Instead, we will give a simpler argument to bound $$$f(n)$$$. Fix some choice of $$$k$$$, and consider the generating functions
The perimeter conditions imply that $$$(1 + x^k) B(x) = A(x)$$$. In other words, $$$k$$$ may only be valid if $$$(1 + x^k)$$$ divides $$$A(x)$$$. Therefore, we can use cyclotomic polynomials for $$$1 + x^k \mid x^{2k} - 1$$$ to determine that
As the degree of the $$$k$$$-th cyclotomic polynomial is $$$\phi(k)$$$ for the Euler totient function $$$\phi$$$, we can see that $$$f(n)$$$ is also at most the maximum number of $$$k_i \leq n$$$ we can select with $$$\sum_i \phi(k_i) \leq n$$$. Since $$$\phi(n) \geq \frac{n}{\log \log n}$$$, this tells us that
and this looser bound already yields a time complexity of at most $$$O(n \sqrt n \cdot \log \log n).$$$ While this concludes the official solution, there exist many other heuristics with different $$$f(n)$$$ that also work.
It is in the spirit of the problem to admit many alternate heuristics that give small enough $$$f(n)$$$ ``in practice'', as the official solution uses hashing. One such heuristic found by testers is as follows:
We take as our pruning criteria that the area of the subdivided polyomino $$$\sum_{i=1}^{n-k} b_i$$$ is exactly half of the area of the original polyomino, which is $$$\sum_{i=1}^n a_i$$$. Algebraically manipulating $$$\sum_{i=1}^{n-k} b_i$$$ to be a linear function of $$$a_i$$$ shows it to be equal to
The calculation of all these sums may be sped up with prefix sums, and therefore pruning of $$$k$$$, can be done in amortized $$$O(n \log n)$$$ time since any fixed choice of $$$k$$$ has $$$\frac nk$$$ segments.
However, for this choice of pruning, it can actually be shown that $$$f(n) \geq \Omega(d(n))$$$, where $$$d(n)$$$ is the number of divisors of $$$n$$$. This lower bound is obtained at an even-sized diamond polyomino, e.g.
Despite our efforts, we could not find an upper bound on $$$f(n)$$$ in this case, though we suspect that if it were not for the integrality and bounding constraints $$$a_i \in {1, \dots, 10^9}$$$, then $$$f(n) = \Theta(n)$$$, with suitable choices of $$$a_i$$$ being found using linear programs. Nevertheless, the solution passes our tests, and we suspect that no countertest exists (though hacking attempts on such solutions would be interesting to see!).
#include <bits/stdc++.h>
#define f first
#define s second
typedef long long int ll;
typedef unsigned long long int ull;
using namespace std;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
void print_set(vector<int> x) {
for (auto i : x) {
cout << i << " ";
}
cout << endl;
}
void print_set(vector<ll> x) {
for (auto i : x) {
cout << i << " ";
}
cout << endl;
}
bool connected(vector<ll> &U, vector<ll> &D) {
if (U[0] > D[0]) return 0;
for (int i = 1; i < U.size(); i++) {
if (U[i] > D[i]) return 0;
if (D[i] < U[i-1]) return 0;
if (U[i] > D[i-1]) return 0;
}
return 1;
}
bool compare(vector<ll> &U1, vector<ll> &D1, vector<ll> &U2, vector<ll> &D2) {
if (U1.size() != U2.size()) return 0;
if (!connected(U1, D1)) return 0;
for (int i = 0; i < U1.size(); i++) {
if (U1[i] - D1[i] != U2[i] - D2[i]) return 0;
if (U1[i] - U1[0] != U2[i] - U2[0]) return 0;
}
return 1;
}
bool horizontal_check(vector<ll>& U, vector<ll>& D) {
if (U.size() % 2) return 0;
int N = U.size() / 2;
auto U1 = vector<ll>(U.begin(), U.begin() + N);
auto D1 = vector<ll>(D.begin(), D.begin() + N);
auto U2 = vector<ll>(U.begin() + N, U.end());
auto D2 = vector<ll>(D.begin() + N, D.end());
return compare(U1, D1, U2, D2);
}
bool vertical_check(vector<ll>& U, vector<ll>& D) {
vector<ll> M1, M2;
for (int i = 0; i < U.size(); i++) {
if ((U[i] + D[i]) % 2 == 0) return 0;
M1.push_back((U[i] + D[i]) / 2);
M2.push_back((U[i] + D[i]) / 2 + 1);
}
return compare(U, M1, M2, D);
}
ll base = 2;
ll inv = 1000000006;
ll mod = 2000000011;
vector<ll> base_pows;
vector<ll> inv_pows;
void precompute_powers() {
base_pows.push_back(1);
inv_pows.push_back(1);
for (int i = 1; i <= 300000; i++) {
base_pows.push_back(base_pows.back() * base % mod);
inv_pows.push_back(inv_pows.back() * inv % mod);
}
}
ll sub(vector<ll> &hash_prefix, int a1, int b1) {
return ((mod + hash_prefix[b1] - hash_prefix[a1]) * inv_pows[a1]) % mod;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
precompute_powers();
int T; cin >> T;
while (T--) {
int N; cin >> N;
vector<ll> U(N), D(N), H(N);
vector<pii> col_UL(N), col_DR(N+1);
vector<ll> hash_prefix_U(N), hash_prefix_D(N);
for (int i = 0; i < N; i++) {
cin >> U[i] >> D[i];
H[i] = D[i] - U[i] + 1;
col_UL[i] = {i,U[i]};
col_DR[i] = {i+1,D[i]+1};
}
// hashing
for (int i = 1; i < N; i++) {
hash_prefix_U[i] = (((mod + U[i] - U[i-1]) * base_pows[i-1])
+ hash_prefix_U[i-1]) % mod;
}
for (int i = 1; i < N; i++) {
hash_prefix_D[i] = (((mod + D[i] - D[i-1]) * base_pows[i-1])
+ hash_prefix_D[i-1]) % mod;
}
// horizontal split
if (horizontal_check(U, D)) {
cout << "YES" << endl;
goto next;
}
// vertical split
if (vertical_check(U, D)) {
cout << "YES" << endl;
goto next;
}
for (int _ = 0; _ < 2; _++) {
// down-right split
for (int c = 1; c <= N/2; c++) {
// check upper portion
if (sub(hash_prefix_U, 0, c-1) != sub(hash_prefix_U, c, 2*c-1)) continue;
if (H[0] - U[2*c] + U[2*c-1] != U[c-1] - U[c]) continue;
// check lower portion
if (sub(hash_prefix_D, N-c, N-1) != sub(hash_prefix_D, N-2*c, N-c-1)) continue;
if (H[N-1] + D[N-2*c-1] - D[N-2*c] != D[N-c-1] - D[N-c]) continue;
// check main portion
if (sub(hash_prefix_U, 2*c, N-1) != sub(hash_prefix_D, 0, N-2*c-1)) continue;
// brute force section
// polynomial division
bool ok = 1;
vector<ll> H_copy(H.begin(), H.end());
vector<ll> quotient(N);
// calculate quotient
for (int i = 0; i < N-c; i++) {
quotient[i] = H_copy[i];
H_copy[i+c] -= H_copy[i];
if (quotient[i] < 0) ok = 0;
}
// check for no remainder
for (int i = N-c; i < N; i++) if (H_copy[i]) ok = 0;
if (!ok) continue;
// construct subdivision
vector<ll> U1, D1, U2, D2;
for (int i = c; i < N; i++) {
int ref_height = quotient[i-c];
U1.push_back(D[i-c] - ref_height + 1);
D1.push_back(D[i-c]);
U2.push_back(U[i]);
D2.push_back(U[i] + ref_height - 1);
}
if (compare(U1, D1, U2, D2)) {
cout << "YES" << endl;
goto next;
}
}
// flip and go again!
swap(hash_prefix_U, hash_prefix_D);
swap(U, D);
for (int i = 0; i < N; i++) {
U[i] = -U[i];
D[i] = -D[i];
}
}
cout << "NO" << endl;
next:;
}
return 0;
}








 $$$\ \ \ \,$$$
$$$\ \ \ \,$$$  $$$\ \ \ \,$$$
$$$\ \ \ \,$$$  $$$\quad\,$$$
$$$\quad\,$$$  $$$\quad\ $$$
$$$\quad\ $$$  $$$\ \ \ $$$
$$$\ \ \ $$$
