If don't want to read full problem at the end I have tried to give short description of problem.

This problem was asked in hackerrank contest, i was unable to solve please help

Problem Statement : MotherCoders is a non-profit organization whose mission is to help women with kids on-ramp to careers in tech so they can thrive in a digital economy. As part of a campaign to help moms break into tech, they are using an unweighted tree to reach new mothers at companies joining work after maternity leave. The goal is to visit all mothers who are joining back after maternity leave across a company hierarchy by traversing a tree (organization) through its nodes (employees), and find the most optimal way to do so. More formally, given an unrooted unweighted tree of n nodes, it is needed to travel from node 1 to node n by following a path. It is compulsory to visit a set of nodes visitNodes in the path followed.

Thus, the path must follow the given conditions:

• The path starts at node 1.

• The path ends at node n.

• The path can visit each node any number of times.

• Each node in visitNodes must be visited at least once in the path.

• From a current node, it is possible to travel to an adjacent node.

Among all such paths, find the minimum length path and return the length of this path. Given an unrooted unweighted tree of n nodes, and an array visitNodes[] of length m, find the minimum length of the path from node 1 to node n such that it visits all the nodes among visitNodes (in any order) at least once.

Note: All the elements in visitNodes are unique.

for example : given:

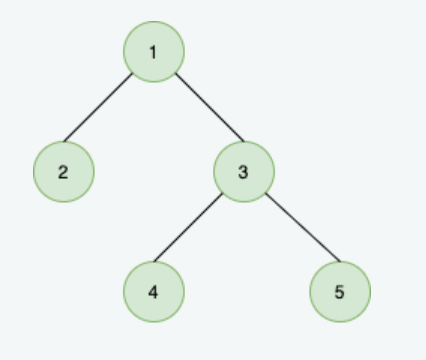
and set of visitNodes = [2, 4]

output : 6 output is obtained by following path 1->2->1->3->4->3->5

Input format : n --> no. of nodes

edges --> 2d array consisiting of edges (of size n-1 considering tree)

visitNodes --> array of nodes that are compusary to visit

Output: return a single integer which is total minimum distance

Short Problem Description : given an unrooted unweighted tree of n nodes and set of nodes that are compulsory to visit, we have to travel through tree starting from 1st node, visiting all the compulsory nodes and end at last node (as 5th node in above example is last node)

Problem : 999E — Reachability from the Capital

This solution was given in tutorial, I understood the approach but i am not getting the time complexity, please help

#include <bits/stdc++.h>

using namespace std;

const int N = 5010;

int n, m, s;
vector<int> g[N];
bool used[N];
bool ok[N];

int cnt;

void dfs1(int v) {
	ok[v] = true;
	for (auto to : g[v])
		if (!ok[to])
			dfs1(to);
}

void dfs2(int v) {
	used[v] = true;
	++cnt;
	for (auto to : g[v])
		if (!used[to] && !ok[to])
			dfs2(to);
}

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	cin >> n >> m >> s;
	--s;
	for (int i = 0; i < m; ++i) {
		int x, y;
		cin >> x >> y;
		--x, --y;
		g[x].push_back(y);
	}
	
	dfs1(s);
	
	vector<pair<int, int>> val;
	for (int i = 0; i < n; ++i) {
		if (!ok[i]) {
			cnt = 0;
			memset(used, false, sizeof(used));
			dfs2(i);
			val.push_back(make_pair(cnt, i));
		}
	}
	sort(val.begin(), val.end());
	reverse(val.begin(), val.end());
	
	int ans = 0;
	for (auto it : val) {
		if (!ok[it.second]) {
			++ans;
			dfs1(it.second);
		}
	}
	
	cout << ans << endl;
	
	return 0;
}

.