Tutorial is loading...
Prepared by Asymmetry
Tutorial is loading...
Prepared by Markadiusz Tutorial is loading...
Prepared by Asymmetry Tutorial is loading...
Prepared by Markadiusz, Monogon and Asymmetry Tutorial is loading...
Prepared by Markadiusz Tutorial is loading...
Prepared by Markadiusz Tutorial is loading...
Prepared by Asymmetry and Markadiusz Tutorial is loading...
Prepared by Asymmetry










I think 1572C - Покраска is actually just 2021 USACO Gold February P2 if you reverse time and apply operations "backwards." The USACO problem starts unpainted, but we can just subtract 1 from our answer in the USACO problem to get something equivalent to 1572C. Also, the operation in 1572C and USACO aren't exactly inverses of each other; namely, 1 USACO operation can do everything that 1 inverse 1572C operation can do, but the reverse does not hold. However, the cases in which the two operations aren't inverses shouldn't affect the answer and I am too lazy to prove it.
They seem very simillar, but I think that the main difficulty of 1572C - Покраска was using the fact that a color may appear at most 20 times.
I just wrote the following Hinted solution to Div1C/Div2E in response to this comment by Penguin07, since this editorial didn't seem to be published when I started. Since I know many people like hinted editorials, I will post it here now anyway.
One obvious plan of attack is DP: Let $$$dp[i][j][c]$$$ be equal to the minimum number of operations needed to make every pixel in $$$[i .. j]$$$ have color $$$c$$$. But even without thinking about what the appropriate transitions might be, it's obvious that this will be way too slow. How can this be made faster?
For each non-empty interval $$$[i .. j]$$$ there will be some set of colors $$$S_{i, j}$$$ and some $$$k_{i, j}$$$ such that
But we don't really care about $$$S_{i, j}$$$ or $$$c$$$. Is there any way to eliminate them?
Try to find some specific color that must belong to $$$S_{i, j}$$$.
It turns out that $$$a_i$$$ is always in $$$S_{i, j}$$$. In fact, there always exists an optimal recoloring of $$$[i..j]$$$ such that pixel $$$i$$$ is never recolored. This can be proven by induction, considering the first operation in any sequence that makes the interval monochromatic.
Suppose there are $$$x$$$ operations. There are several trivial cases: The base case of $$$x = 0$$$; the case where the first operation only affects pixels to the right of $$$i$$$, where the remaining $$$x-1$$$ operations may be replaced without issue; and the case where the first operation only affects pixels to the left of $$$i$$$, in which case the operation may be discarded since only pixels in $$$[i..j]$$$ influence the result of operations on pixels in $$$[i..j]$$$.
Otherwise, the first operation modifies some contiguous interval $$$L$$$ of pixels that includes $$$i$$$. Let $$$R := [i..j] \setminus L$$$ be the rest of the relevant interval. Then, the remaining $$$x-1$$$ operations make $$$R$$$ monochromatic, so by the induction hypothesis there exists a sequence of at most $$$x-1$$$ operations which make $$$R$$$ monochromatic but do not modify its leftmost pixel or any further-left pixel. Then, since the first operation did not affect the interval $$$R$$$, the whole sequence may be replaced by the $$$x-1$$$ operations making $$$R$$$ monochromatic (but not affecting $$$L$$$) followed by at most one operation recoloring $$$R$$$ to match $$$L$$$.
(This proof is constructive and works in $$$O(x \alpha(x) + j - i)$$$ if the underlying recoloring operations are simulated with a DSU-forest.)
Remember the unusual constraint that "For each color, the number of pixels of that color is at most $$$20$$$." This suggests that we may only need to consider splitting the $$$[i..j]$$$ interval at pixels with initial color equal to $$$a_i$$$.
For any minimum-length sequence of operations that makes $$$[i..j]$$$ monochromatic, there must exist some $$$x \in [i..j]$$$ such that pixel $$$x$$$ is never recolored. This can be proven by contradiction, considering the first operation such that the pixels it recolors are never subsequently recolored in any counterexample.
The base case of a length-one interval is trivial. Otherwise, suppose that first operation which recolors pixels never subsequently recolored colors some interval $$$M = [x..y]$$$ previously of color $$$c$$$. Then, let $$$L := [i..x-1]$$$ and $$$R := [y+1..j]$$$. The goal is to re-color $$$L$$$ and $$$R$$$ to color $$$c$$$ without any extra operations or clobbering of $$$M$$$, thus saving the need to ever recolor $$$M$$$ in the first place.
Note that $$$L$$$ or $$$R$$$ may be empty, but this case is trivial. Otherwise, by assumption every pixel in $$$L$$$ and $$$R$$$ gets subsequently re-colored at least once. Therefore, by the induction hypothesis (since $$$L$$$ and $$$R$$$ are shorter than $$$[i..j]$$$), there exists a strictly shorter sequence of operations in each of $$$L$$$ and $$$R$$$ which makes each one monochromatic. By the result of Hint 4 (and its mirror-image for $$$L$$$), it may be assumed that these strictly shorter sequences of operations do not affect the color of $$$M$$$ and do not interfere with one another, so that they may be combined. Finally, the one operation saved on each side may be spent re-coloring the now-monochromatic $$$L$$$ and $$$R$$$ to have color $$$c$$$, matching $$$M$$$ and thus making all of $$$[i..j]$$$ monochromatic.
(This proof is also constructive, but not as efficiently so: It needs to invoke the proof of Hint 4 up to $$$O(j-i)$$$ times.)
Suppose for convenience that the input data has been pre-processed to contain no consecutive pixels of equal color. Consider any interval $$$[i..j]$$$ of length at least two, and minimum-length sequence of operations which make pixels in an interval $$$[i..j]$$$ all have color $$$a_i$$$. By hints 2 and 4, this has length $$$k_{i, j}$$$, and the answer to the problem is $$$k_{1, n}$$$.
By hint 6, there must be at least one pixel in $$$[i..j]$$$ which is never recolored. If $$$i$$$ is the only such pixel, then it is a recoloring of $$$[i+1 .. j]$$$ to color $$$a_i$$$, and recolors every pixel in that interval at least once. Thus, by hints 2 and 6, it has length at least $$$k_{i+1, j} + 1$$$. Otherwise, let $$$x$$$ be the left-most pixel in $$$[i+1 .. j]$$$ which is not recolored. Then, the sequence consists of (A) a recoloring of $$$[i+1 .. x-1]$$$ to color $$$a_i$$$ which recolors every pixel in that interval at least once, and (B) a minimum-length recoloring of $$$[x .. j]$$$ to color $$$a_i$$$. By hints 2 and 6, (A) takes at least $$$k_{i+1, x-1} + 1$$$ operations. Since $$$a_x$$$ must equal $$$a_i$$$ as pixel $$$x$$$ is never recolored but ends up with color $$$a_i$$$, (B) takes $$$k_{x, j}$$$ operations. Since pixel $$$x$$$ is never recolored, parts (A) and (B) are independent of one another, so that the total number of operations is at least $$$k_{i+1, x-1} + 1 + k_{x, j}$$$.
Conversely, it is clearly possible to construct solutions of length $$$k_{i+1, j} + 1$$$ or of length $$$k_{i+1, x-1} + 1 + k_{x, j}$$$ for any $$$x \in [i+1 .. j]$$$ with $$$a_x = a_i$$$, so $$$k_{i, j}$$$ must be equal to the minimum of these values.
It should be clear that the number of transitions in this DP is $$$O(n^2 \cdot \text{max occurrences of any single color})$$$, which is fast enough with a reasonable implementation.
EDIT 1: fixed link, fixed notation in hint 3
EDIT 2: added slightly stronger claim and proof to hint 4; fixed notation $$$a[i]$$$ -> $$$a_i$$$ in solution; moved edit summaries
EDIT 3: completely rephrased hint 1; removed some not-a-priori-obvious "minimum-length"s under solution, replacing them with "at least" as necessary
EDIT 4: fixed/replaced proof for hint 4; added proof for hint 6
Thanks a lot for the explanation. I really didn`t understood anything in editorial, but your solution is nice and clear.
looking for proof of first hint.
Why dp will give legitimate painting? Why colors can't overflow interval? Why can't them block each other? And in the end, I guess you suppose you don't repaint any segment before joining to other. Why this is not required?
I'm not sure I understand. As I don't make or use any claims anywhere about how to calculate the values I suggest in hint 1, there's nothing to prove.
I was very careful about the repaint-before-joining concern, because I shared that concern. Off the top of my head, I'm not sure of a better way to prove that these aren't necessary than "This solution is optimal. Oh, look, it doesn't actually perform any non-joining repaints." (That's not to say that no easier proof exists!) Please let me know of any step where you think I may have inadvertently used this assumption, or any other.
This doesn't look valid argument to me. How can you look? As far as I understand, that dp calculation assume that you combine two or three subintervals. You can't claim that it's always two subintervals, because this thing should be proven. Then, in order to paint whole segment, you have to claim that you can paint first subinterval into first color, then second subinterval into second color, and if there is third subinterval, then color it into third color. Suppose you successfully painted first subinterval into first color. Why would we successfully color second subinterval into second color? It could possibly already have been messed by all previous actions over first subinterval? Because I think they could overflow bounds of first subinterval, and thus its coloring sequence now meaningless.
It's pretty trivial: You repaint the second interval first. No recomposition step on interval $$$[i..j]$$$ will ever mess with pixel $$$i$$$ or any lower-numbered pixel. This can be seen as a slightly stronger version of Hint 4.
EDIT: But I agree in hindsight that I should have provided more detail in the proof of hint 4, since there are a few ways to go wrong. I will add this to my original comment.
EDIT2: This is done.
Hypothesis of induction: color $$$a_l$$$ is among colors in which [l,r] can be paint into single color in minimum steps. And, also, we can paint into $$$a_l$$$ color whole [l,r] segment never painting position $$$l$$$. Base of induction: length of interval is 1. Obviously minimum required steps = 0 and it already has color $$$a_l$$$. Step of induction: We know that for length of interval n — 1 is proven. We have to prove for interval of length n.
Let's pick optimal sequence that paint [l,r] into single color. Let's say its length is M. Look at last operation. Let say before it [l,r] would look like [l,i] of color $$$c_1$$$ and [i+1,j] of color $$$c_2$$$ and [j+1,r] of color $$$c_1$$$. Then we paint $$$c_2$$$ into $$$c_1$$$, so this whole thing becomes color $$$c_1$$$. Even though there is only 2 colors, their relationship with corresponding $$$S_{l,i}, S_{i+1,j}, S_{j+1,r}$$$ may take 9 options.
I stuck in following case:
In this case, length of sequence $$$M \geq k_{l,i} + k_{i+1,j} + k_{j+1,r} + 1$$$. Prove this inequality by contradiction. Suppose length of sequence is smaller. Then each step of sequence change at most one of intervals [l,i] or [i+1, j] or [j+1, r]. Let total changes of interval [l,i] to be A, and total changes of interval [i+1, j] to be B, and total changes of interval [j+1, r] to be C, not taking into account their join. Then $$$A + B + C + 1 \leq M$$$. But if we concentrate our look at corresponding intervals, we know $$$A \geq k_{l,i},\; B\geq k_{i+1,j},\; C\geq k_{j+1,r}$$$ by definition of $$$k$$$. In other words, we can't paint them in single color faster with longer array, because it didn't ever paint from outside. Now make sum of this inequalities. We get $$$A + B + C \geq k_{l,i} + k_{i+1,j} + k_{j+1,r}$$$. Thus $$$ M \geq A + B + C + 1 \geq k_{l,i} + k_{i+1,j} + k_{j+1,r} + 1$$$. But we supposed $$$M < k_{l,i} + k_{i+1,j} + k_{j+1,r}$$$. This is contradiction.
Now we know for sure, that $$$M \geq k_{l,i} + k_{i+1,j} + k_{j+1,r} + 1$$$. But what if $$$M = k_{l,i} + k_{i+1,j} + k_{j+1,r} + 1$$$ the case? Could it be such that $$$a_l \neq a_{j+1}$$$, so we know how to make first and last segments into not-equal colors without touching $$$l$$$ and $$$j+1$$$ correspondingly, but there exists $$$c_1$$$ that $$$c_1 \in S_{l, i}, \; c_1 \in S_{j+1,r}$$$? Then we don't know how to paint this interval.
Right. The last operation doesn't work: In order to replace a 3-way merge efficiently, we need the right-most color to match the left-most color, and have no way to control the colors available in the right-most interval. The worst-case looks something like this:
To avoid this problem, I need to scrutinize and replace some operation that cannot result in a 3-way merge in $$$[i..j]$$$. Luckily, in any counter-example, there must be one: The operation that modifies pixel $$$i$$$. I've fixed/replaced the proof in Hint 4 to hopefully not be broken, and added a proof to Hint 6 as well.
Let me know if you spot any other oversights.
Well, I completely agree with proof in hint 4. You're genius! I was trying to prove anything for past three days with no luck. There is tricky order of induction though.
It doesn't prove what it meant to prove. Trouble is with M that may in original sequence expand by last coloring.
When you'll count, using induction (actually contraposition to induction hypothesis) we have suboptimal number of operations for L and R, because of their suboptimality you can replace them at least by one shorter, but you need to take into account that expanded
dinto region of L as an operation. You can't claim now that recoloring of M is separate 1 paint. So M of our sequence now is suboptimal by L, and suboptimal by R, but without additional step of recoloring M, it's mixed in suboptimality of L. But in case when M doesn't expand that's true. I think it's proof that painting without change of borders is always suboptimal. And then, you simply can build tree where each node has child-color into which it was painted, thus x indeed exists (just walk towards leaf).Edit: no, not so easy, it's not proof that painting without change of borders is always suboptimal. Because we use fact that L and R is recolored, but there can be many places without recoloring
Re: Proof of Hint 6: The recoloring of $$$M$$$ can't partially merge it with any other region, because that region is recolored later but $$$M$$$ is not.
In proof of hint 6 you say color c is color of M before repaint. But M itself is before repaint or after? Because before last repaint it could have shorter length. If it's before repaint, then it's how I thought initially in previous reply. If M is after last repaint and L and R is also after, then let S be before repaint. Then union of L, R and S is not whole interval. Whole interval is union of L, R, M. You provide sequence to paint union L, R, S.
I intended it to mean $$$M_\text{before}$$$, as otherwise "previously of color $$$c$$$" doesn't make a lot of sense. But actually, $$$M_\text{before} = M_\text{after}$$$, since it is impossible for the original sequence to later recolor any cell in $$$M_\text{after}$$$ without also recoloring every cell in $$$M_\text{before}$$$.
That said, this property of $$$M$$$ shouldn't matter: The induction hypothesis and the non-clobbering guarantees from Hint 4 apply to the intervals $$$[i..x-1]$$$ and $$$[y+1..j]$$$ even if they do not respect region boundaries. The important thing is that the non-repaintedness of $$$M$$$ prevents the original sequence from being able to share work between $$$L$$$ and $$$R$$$. (So, this proof does NOT work on a circle, for example.)
I just wanted to tell right before you made reply that I got it. But reason is different. By contradiction, in case it enlarged into $$$M_{after}$$$ by recoloring, then joined part will never recolored, and didn't colored with this action. Thus, it was recolored earlier — we found earlier action that did recolor never-recolored-afterwards segment. Thus, our initially considered action wasn't first one of kind. Contradiction with assumption that it was earliest.
here's a nice alternate solution to Div.1 E that comes up intuitively but is surprisingly hard to prove.
Let's binary search for the answer. For some number $$$t$$$, we want to know if the polygon can be cut into at least $$$k+1$$$ regions, such that each region has double area $$$\ge t$$$. Call a configuration of cuts "valid" if it satisfies that condition.
Consider the dual graph of the regions that the polygon is cut into. In other words, we construct a graph such that each region is a vertex, and connect two regions with an edge iff there is a cut separating them.
Lemma 1. If there exists a valid configuration, then there is one valid configuration where the maximum degree of a vertex is at most 3.
To prove this, we need another lemma:
Lemma 2. Suppose a vertex in some configuration has degree at least 3: if region $$$X$$$ is adjacent to regions $$$A$$$, $$$B$$$, and $$$C$$$, then $$$\operatorname{area}(X) > \min(\operatorname{area}(A),\operatorname{area}(B),\operatorname{area}(C))$$$.
This seems pretty obvious if you draw the diagram. To actually prove this, we can utilize task 9.1 (on page 80) from [this book](https://www.isinj.com/mt-usamo/Geometric%20Inequalities%20-%20Bottema,%20et.%20al.%20(1968).pdf) (credits to mnbvmar for providing this). This margin is too small to contain the detailed proof, so I leave this as an exercise to the reader.
Now we go back to Lemma 1. Suppose a region $$$X$$$ has degree $$$d\ge 4$$$, and is adjacent to regions $$$A_1,A_2, \dots, A_d$$$. Then we can cut $$$X$$$ in two regions $$$X_1$$$ and $$$X_2$$$ such that they are both adjacent to at least two regions in $$$A_{1\dots d}$$$. WLOG, let $$$\operatorname{area}(X_1) \le \operatorname{area}(X_2)$$$. Since $$$X_1$$$ has degree at least 3, by lemma 2, we have $$$\operatorname{area}(X_1) > \min(\{\operatorname{area}(A_i) \mid A_i \text{ is adjacent to } X_1\} \cup \{\operatorname{area}(X_2)\})$$$, so $$$\operatorname{area}(X_2) \ge \operatorname{area}(X_1) > t$$$. This means that the configuration after cutting $$$X$$$ is also valid.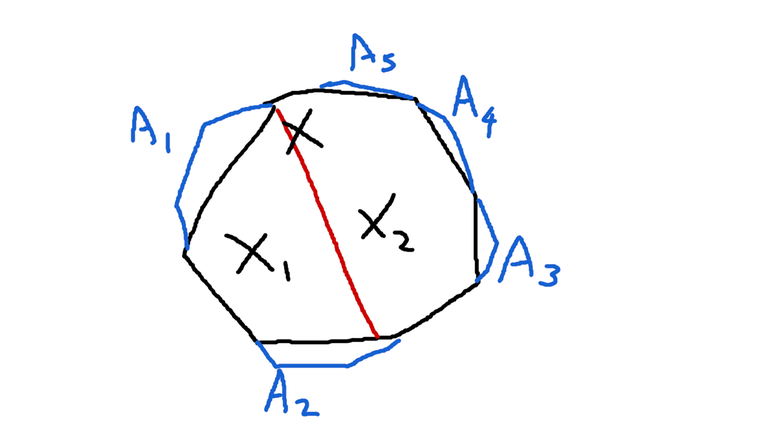 After applying the procedure, the number of vertices whose degree $$$\ge d$$$ decreases, so if we repeat it enough times we will obtain a configuration where every degree is at most 3. QED
After applying the procedure, the number of vertices whose degree $$$\ge d$$$ decreases, so if we repeat it enough times we will obtain a configuration where every degree is at most 3. QED
Now back to the solution. For $$$1 \le l,r \le n$$$, consider the sub-polygon with vertices in the interval $$$[l, r]$$$, wrapping around (i.e., vertices $$$l,l+1,\dots,r$$$, or $$$l,l+1,\dots,n,1,2,\dots,r$$$ if $$$l > r$$$). Let $$$dp[l][r]$$$ be the maximum number of regions we can cut that sub-polygon into, such that each region has area $$$\ge t$$$ (initialized to 0). Due to lemma 1, we only need to consider the cases where the maximum degree of regions is 3, so there are three ways to obtain $$$dp[l][r]$$$:
Each step can be done in linear time. Case 3 can be done in linear time by using two pointers, or by maintaining an additional array $$$minl$$$, where $$$minl[a][b]$$$ is the minimum number $$$c$$$ such that $$$dp[a][a+c] \ge b$$$.
We can precompute the areas of sub-polygons in $$$\mathcal{O}(n^2)$$$, and update $$$dp$$$ in a bottom-up manner (from the smallest to largest intervals). Finally, the number $$$t$$$ satisfies the binary search condition iff $$$dp[l][r] + dp[r][l] \ge k+1$$$ for some $$$l,r$$$. (Taking $$$dp[0][n-1]$$$ directly doesn't work, see below)
The time complexity for each binary search iteration is $$$\mathcal{O}(n^3)$$$. However, it has a larger constant factor than the official solution, because we have to consider all pairs $$$(l,r)$$$ instead of only those with $$$l \le r$$$. tourist's contest submission (129206504) is the only one using this approach, and it almost got TLE (2994ms / 3000ms).
A lot of minor, tedious details were left out, but they should be quite easy to see.
Ackchyually, you might notice that the DP above is not always correct... However, the final step will always give the correct answer!
In case 2, consider the following diagram: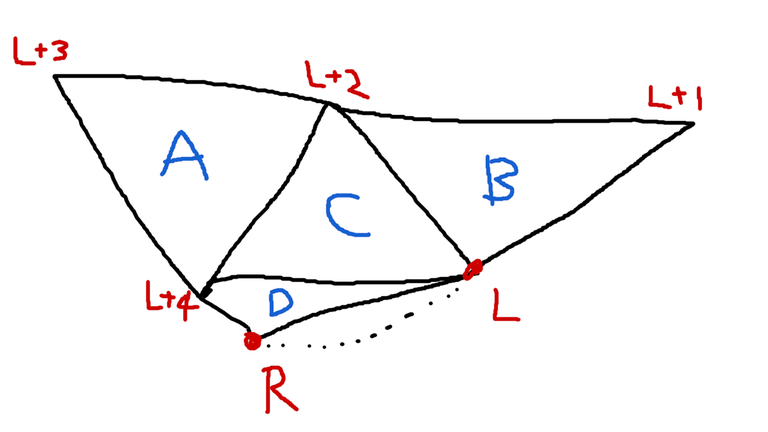 Where the areas satisfy $$$t=C+D=A=B>C$$$. When we write the DP values out, we can see that the answer of $$$dp[L][R]$$$ should be 3, but in the above algorithm it is set to 2! The correct version of case 2 should not only consider triangles, but all polygons with degree 2 instead.
Where the areas satisfy $$$t=C+D=A=B>C$$$. When we write the DP values out, we can see that the answer of $$$dp[L][R]$$$ should be 3, but in the above algorithm it is set to 2! The correct version of case 2 should not only consider triangles, but all polygons with degree 2 instead.
But why does this not break the solution? Observe that if case 2 fails, then in the final step we will always be able to find another interval where the DP is correct, and construct a valid configuration.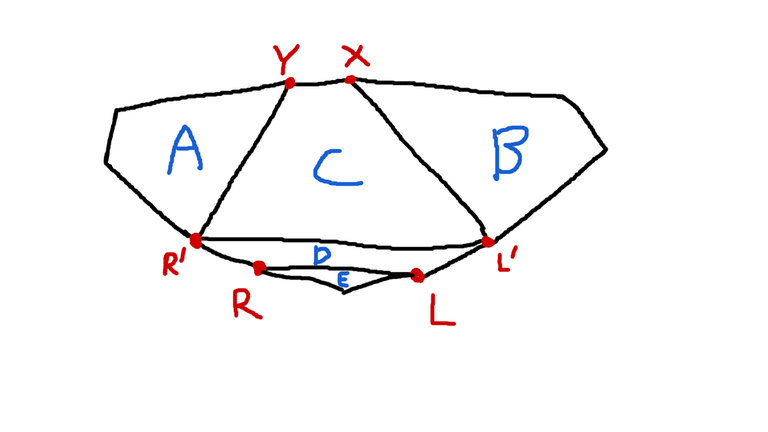 Let's consider the more general case above. Suppose that here $$$dp[L^\prime][X],dp[Y][R^\prime] \ge 1$$$ and $$$dp[L][R]$$$ is incorrect in case 2. This implies that $$$\operatorname{area}(\triangle L^\prime R^\prime X)\le t$$$ (otherwise $$$dp[L^\prime][R^\prime]$$$ would be correct and so would be $$$dp[L][R]$$$), and by lemma 2 we have $$$\operatorname{area}(D)+\operatorname{area}(E) \le t$$$. This means that $$$dp[R^\prime][L^\prime]=0$$$, so $$$dp[X][L^\prime]$$$ can be correctly computed -- giving us a valid construction ($$$dp[X][L^\prime]+dp[L^\prime][X]$$$ is correct).
Let's consider the more general case above. Suppose that here $$$dp[L^\prime][X],dp[Y][R^\prime] \ge 1$$$ and $$$dp[L][R]$$$ is incorrect in case 2. This implies that $$$\operatorname{area}(\triangle L^\prime R^\prime X)\le t$$$ (otherwise $$$dp[L^\prime][R^\prime]$$$ would be correct and so would be $$$dp[L][R]$$$), and by lemma 2 we have $$$\operatorname{area}(D)+\operatorname{area}(E) \le t$$$. This means that $$$dp[R^\prime][L^\prime]=0$$$, so $$$dp[X][L^\prime]$$$ can be correctly computed -- giving us a valid construction ($$$dp[X][L^\prime]+dp[L^\prime][X]$$$ is correct).
Congratulations to tourist for winning the contest, and solving E with this solution that is very hard to prove!
There used to be another solution that uses some observations above, and also relies on the following assumption:
Conjecture 1. If there exists a valid configuration, then there is one valid configuration where at most one region has degree $$$\ge 3$$$.
However, this is unfortunately not true: I disproved it by a counterexample (see test #32). Interestingly, this doesn't break my solution above, not even in the "sike" section.
implementation: 129215696
For Div1 A, I think Topological sort isn't needed when we are using DP in DAG. We can just iterate on nodes in a random fashion and use DFS with DP to calculate the longest path
Note that the process you've described simulates toposort. If a node v is reachable from node u, they either lay on the same cycle, or v belongs to a SCC reachable from u's SCC. In short, sometimes topologically sorting the graph explicitly is not necessary.
Not necessarily. It will be topological sort if and only if we are picking the right root randomly. Example, we have edges from 1 to 2 and 2 to 3, then topological based DFS will always start from 1 whereas a random traversal can start from anywhere. And in this problem, the order in which you pick the nodes/roots isn't important
As the order of nodes isn't important for calculation of our DP, we only need to calculate dp[x] after it is calculated for all the nodes that would appear later in the topological sorting of the graph, which is ensured by the DFS itself.
That is the property of the DFS itself, and since it's pretty implicit, we don't need to mention the need of toposort like that, because highly likely that the readers of the editorial may relate it to the order of picking roots (which will obviously work, but an overkill)
This edge has weight 0 if a<b and 1 otherwiseShouldn't the weights be vice versa?Consider the graph 1->2->3->4->5 According to the given model, all the weights will be 0 and answer as 1 but the answer is 5 and all weights should be 1 for this.
why answer is 5? you can read them in one cycle 1,2,3,4,5.
Thanks for pointing out that typo. It should be correct now.
I never believe that I will one day say this to a flow problem, but D (div 1) is great. After the contest I've talked to some people about it, and most of their thought processes involve somehow optimizing the finding-the-blocking-flow operation (which one of them apparently managed to do). I am glad to see that instead of some obscure trick written in Chinese/Polish/Russian paper #1257, the key to the solution lies in a simple observation. Kudos to the authors for coming up with such a nice problem.
Can anyone help me with the problem 1572A - Книга?? My solution is giving wrong answer in test case 2. I have used topological sort.
My solution — 129302238
IMO the problem is that for each chapter of the book (nodes if you suppose its a graph) you have to check all the ones on its require list. but you only check the last one in the topological order. since my solution is pretty much like yours, i recommend you to check it out: [](https://codeforces.me/contest/1573/submission/129306114)
You were right. I was updating only for the last element of topological sort.
Accepted solution (if anyone need) — 129310560
Thanks a lot mani100011
Can you please explain what your dp vector stores? And, what this lines of code means
int y; if (nx < x) { y = dp[x]+1; } else { y = dp[x]; }Thanks.
div1 A was really interesting!
Hello ,can we solve (DIV2C/DIV1A) problem just by modifying topological sort, you can see my code here Code link.It is giving me the wrong answer. Can you please tell me why?
if(indegrees[nbr]==0&&(nbr>m)){ q.push(nbr); }This line ,nbr>m is incorrect.You need to check this for every parent of nbr which is present in the current 'q' and nbr should be greater than all of them .You can check my code but its giving TLE dont know why
Can you suggest why TLE at test 3 ,I m just using set erase and insert
in your cycle function you should add a single '&' character before adj and it'll be alright.
ya figured it out my bad ,thanks btw
If anyone solved Book (Div 2 C / Div 1 A) with the first approach mentioned in the editorial then can you please send me your code, I'm having a hard time understanding what is written. thanks!
https://codeforces.me/contest/1572/submission/129340066
I think you can refer mine
below are comment on variables.
I appreciate it! Thank you so much !
in which we can find a matching with maximum cost and size at most k with for example one of the standard min cost max flow algorithmsCan someone please explain this part?
Let's assume that after the reduction we are left with edges (1, 5), (4, 5), (4, 6), (2, 6), (2, 10). Then we can make a flow network like so and find min cost max flow from node S_0 to node T in it. Here the first value on an edge is its capacity and the second is its cost. I hope that you can figure out the general approach from this picture.
How to prove that minimum cost always occurs when flow is k?
It’s based on the fact that the weight of an edge $$$w(U, V)$$$ is the sum of the values of the two vertices $$$a_U + a_V$$$. Consider an augmenting path algorithm to calculate maximum weight flow/matching. In order to increase the size of the matching by one, we search for an augmenting path with maximum weight. For example, if edges (B, C) and (D, E) are in the matching, an augmenting path may be (AB), (BC), (CD), (DE), (EF). Its weight is $$$w(AB) - w(BC) + w(CD) - w(DE) + w(EF)$$$. This is equal to the sum of the values of its endpoints, $$$a_A + a_F \geq 0$$$. So, as k increases, the maximum weight of a matching of size k is non-decreasing.
Got it thanks!!
Can anyone prove the optimality of the solution for div2 a?
Well, consider taking a number 2079, so we have to make it 0, either by subtracting 1 or swapping positions. Now first we'll subtract 1, 9 times to make it 2070. After this we've to make 7->0, for this we'll need to subtract 1, 70 times but since we can swap 2 digits , so we'll swap 7 and 0. The main idea being getting every digit to the one's place so that we can make it 0 in min number of operations. For more clarity consider 10, we'll need to subtract 1, 10 times to make it to 00. And so the most optimal way is to swap 1 with 0 and then subtract 1 only once.
I think editorial is poorly written. And that's why I decided to write my alternative editorial with hints and proofs of tasks which I solved or upsolved. Only my solutions (alternative solutions not covered).
1573A - Обратный отсчет
How to decrease number as much as possible by single allowed action?
You need to find first digit standing earlier than smaller digit, and swap them (among smaller pick smallest rightmost). For example 0011352425 become 0011252435. If there is no such pair of digits, then just decrease number by 1.
Proof: decrease by 1 is always decreasing number by 1. In the number ???a??b??? swap a and b is identical to:
So, change is (b-a)*1000000+(a-b)*1000 = (b-a)*(1000000-1000). Number with less number of zeroes is obviously less, so change is (b-a)*(something bigger than zero), thus change is bigger than zero if b-a bigger than zero. Notice that (1000000-1000) >= 900000, so swap to this place will decrease by at least 900000 if b < a. If we swap to digit one digit to right, decrease will be at least by 90000, at most 100000. So picking position of a earlier if we can -> is better. When we chose place of a, now we need to pick place of b. Its position corresponds to 1000, and if it is moved to the right, it becomes to 100, so we want rightmost one.
How to decrease number as much as possible by performing two allowed actions?
Based on all possible orders of actions:
So, here we see new type of action: decrease ending and swap in front.
What will happen if we perform strategy from previous hint? In other words, we will pick best pair of actions, and perform two at once.
After several actions, digits become sorted, and they almost turned into queue for decrease, and after each time we decrease, we move digit back according to sorted order.
Why we bring digits back to sorted? Let them decrease once for all!
Indeed, we don't need to move digits back and forth, so lets not do that. Move zeroes to first non-zero, and decrease non-zero.
It's solution, proof in hits below.
How can we decrease certain non-zero digit?
We can decrease digit either when it's last one, or when there is only zeroes after it. Either way we need at least one action to decrease it.
What if we decrease digit by second case: when there are zeroes after it?
This will make bunch of digit 9 which require at least 9 actions each. (Proof in previous hint). So actions required at least sum of digits.
Do we ever need to decrease when last digit is 0?
No. Hold on. Not so fast. Proof is in hints below.
What if we forbid decrease when last digit is zero? How to optimally solve original task with this modification?
Then strategy is following: decrease last digit until it's zero. If we're done — stop. If there is non-zero digit, swap last zero with it. continue process. Total number of actions = sum of digits + number of non-zero digits except last digit.
What if we allow back action we forbid?
In optimal answer we don't ever need to perform it. Proof is following.
Suppose we need to decrease at least once when last digit is 0. So, there is some sequence of actions, which claimed to be optimal, and it has at least once decrease when last digit is 0. Lets perform same sequence of actions up to last action when last digit is 0, and not perform it! At current state we have number with 0 in the end and it has sum of digits S and non-zero digits D. So we know that it is possible to make all zeroes in S + D steps (by previous hint). If we would perform decrease, we would have sum of digits at least S+8, and number of non-zero digits would not decrease (it may only turn single digit into zero). But by previous hint, optimal solution without performing forbidden action is sum of digits + number of non-zero digits except last digit. And it is at least S+8+D-1 (last digit now 9). In other words, after we perform it, our optimal sequence (which we claim to be optimal) has to be at least S+7+D steps, but if we don't then we know how to make in S+D steps. Contradiction with claim that sequence of actions is optimal. 129221146
In hint 9
1573B - Смена мест
What means that first not-equal position is
i?This means that everything up to position
iis equal.How can it be?
It needs to have at least same first number.
Arrays in this task can't have same first number after any performed actions.
Number x which is first in both arrays should be even and odd simultaneously. Have you ever heard of numbers like that?
But what is less determined by first position which is non-equal. And by previous hint, we just need to make first number of first array to be less than first number of second array.
Suppose we know which number would appear in first array at first position. How to minimize number of actions to move it there?
Let's say it is at position
i, then we should swapiandi-1, theni-2,i-3, theni-3andi-4and so on. Total number of actions required is zero-based index of initial position.Let's mark all other numbers with symbol, for example '?'. For us they are indistinguishable. All we care is about our number we want to bring to beginning. Notice, that each time we swap with previous
?we decrease zero-index position by one. Each time we swap with next?we increase zero-index position by one. Thus, our actions identical to +1 and -1 to zero-index position. But fastest-possible way to get 0 is only perform -1. (You can proof this fact by contradiction considering last performed +1 similarly to proof in previous task).Suppose we know which number would appear in first array at first position, and we also know which number would appear in second array at first position. What is minimum actions required?
Actions in both arrays are independent.
Indeed each time you perform action on first array, you get new version of first array, each time you perform action on second array, you get new version of second array. Action on first array gets previous version of it and makes next version of it. Similarly for second array. So resulting first array depends only on sequence of actions performed on first array. Similarly second array.
This means that we can first do all the actions on the first array, and then on the second array.
Similarly for second array it's just zero-based index of number from second array. So minimum actions required is sum of indices of two numbers we want.
Suppose we know which number would appear in first array at first position. Can we figure out which number is fastest can we pick from second array?
We can pick any number greater than picked number in first array. And among them we need to pick with lowest zero-based index.
For arbitrary u < v from first array. For the number v, all the numbers from which we choose are suitable for the number u.
Suitable numbers for v is some w > v (suitable means it should be greater). But it's also suitable for u, because w > v > u, so w > u.
The lower the number from first array we choose, the more options we have, none of options vanish.
Find positions for all numbers. It can be done in O(n) with single loop. Then, let set of options for second array to be empty. We will maintain minimum zero-based index among all options within this set. Initialize this minimum to infinity. Now, try all numbers from first array in decreasing order. And for each of them, add numbers from second array which become suitable into set of options, and update minimum zero-based index. For this picked value in first array, minimum required actions is to pick maintained minimum from second array + zero-based index of picked value in first array. So update answer if it's better. 129221276
1572A - Книга
What chapter will we understand first?
The chapter which we can understand.
What chapter can we understand?
Chapter with not-yet-understand required chapters = 0.
How many chapters will we understand? Upper-bound
N. In the end, we might understand whole book.
When we read chapter and understand it, on what chapters it does affects? How?
On chapters, that were require this one for understanding. For those chapters now not-yet-understand chapters decrease by 1.
Just simulate process. Maintain chapters that are ready to understand. Also, maintain chapter that will be read right now. Let's call it
pos. All we need to do, is:posfrom chapters ready to understand. Or we finish reading book andposbecome first chapter.For not-yet-understand chapters we can use simple array of counters. Counter at index
iwould tell us how many not-yet-understand chapters require chapterifor understanding. Chapters which we iterate when we read and understand chapter we will store in array of arrays. Array at indexiwould tell which chapters should decrease not-yet-understand counters. Chapters that are ready to understand require fast insert/remove and also search first >=pos. This can dosetin C++ orTreeSetin Java. Python as far as I know doesn't have anything suitable in standard library. 1291776161572B - Xor трех
Consider unlimited number of actions.
Notice, that if array starts with 0, then we can reduce it either to 0 or to single 1.
Indeed, look for first 1, then if next is also 1, we can xor 011 and get 000 there and keep going. if there is 010 look at next character, if it's 0101 then we can xor 101 and get 0000 there. The only remaining case is 0100 where we can xor 100 and get 0111, and xor 011 and get 0001 there. Summary
Notice, we can bring index of first 1 at least by two positions to the right using at most two actions. And the only cases where we can't, is either we end up with array having in the end 01, or 010.
Notice, that parity is invariant. In other words, after action is performed, parity keeps same.
XOR of three elements which are zeroes or ones is basically single bit XOR. For single bit we know that result remainder by two of sum. So (0 XOR 1 XOR 1 XOR 0 XOR 1) is (0 + 1 + 1 + 0 + 1) mod 2 = 1 (where x mod y is remainder of x by y).
Suppose bits are a, b, c. Their parity is (a + b + c) mod 2 = (a XOR b XOR c). They all become d = (a XOR b XOR c). So, new parity is (d XOR d XOR d) = ((d XOR d) XOR d) = (0 XOR d) = d = (a XOR b XOR c). It didn't change.
Also you could check all options.
If we had 0 in first position, and performed strategy from hint 2 and left with single 1, then it's impossible to make all 0.
Parity is invariant, this means that you can't get parity 0 from array with parity 1, and vice versa. This also means, that if you have single 1 in the end, then it initially had parity 1, so it was impossible from the beginning.
This also means we can solve case when first is 0, because we increase index of 1 at least by two using at most two actions. Thus we will need less or equal to n actions.
What if first element is 1 and we have unlimited number of actions?
There are following cases:
So, when we have single 1 in the beginning, you can increase number of 1 by two (decrease number of zeroes by two), or you can increase number of ones after all zeroes by two (it also decrease number of zeroes by two). And in opposite, you can decrease number of ones by 2 in the beginning or in the end.
This in particular means, that if array starts with odd number of ones then there is zero right next to it, then you can eat them into single 1, but not eat all of 1. 111110->111000->100000 And, if array starts with even number of ones in the beginning and there is zero right next to it, then you can eat all 1 to the beginning of array. 1111110->1111000->1100000->0000000.
What if array starts with odd number of 1 and we have unlimited number of actions?
We need, to somehow eat single 1 at tail of this odd number of 1, and then we can make it whole into zeroes. To do that, we can either reach by ones from left or from right:
But, notice we require odd number of zeroes in between. Note! Below I don't focus on case where there is no ones from the right.
What if array starts with odd number of 1 and right next to it is even number of zeroes and we have unlimited number of actions?
For example, we can do 100001->111001->111111. What if we don't?
Assume there is 1000011??? where ? each is either 0 or 1. Then: either:
We either decrease right by 2, or increase right by 2, or increase left by 2, or decrease left by 2. In any way, until we do 101 -> 000 any segment of 111 keeps parity, and any segment of 000 also keeps party. This means we have to do 101->000 to change parity or join two segments. And to find it, easy way is to make 100001->111001->111111 = join ones. If parity becomes even -> nice. Otherwise when we appear in situation where array starts with ones, and right next to them single 0 and single 1, then we do 101->000 and make all 1 to the beginning. Then finish with algorithm for case when array starts with 0.
Notice that each xor we performed was to fill up to 101, and in worst case we could fill everything up to 101. Let say i is zero-based index of first element of 101 we stumbled across. Then we probably did xor at i-2 to get one at position 1, also we probably did xor at i-4, and so on. i has to be even, because number of ones is odd. So numbers of operations in worst case is all even numbers from 0 to i-2 which is i/2. Then we do operation 101->000. Then, we also need to make all ones into zeroes. Number of ones left is i, so it's additional i/2 operations. And in the end it require i/2+1+i/2 = i+1 operations. But now at position i there is 000, so, from i+2 position we have array starting from zero. And our first algorithm for this particular case can turn everything in zeroes in number of actions not exceeding length. Remaining length is N-(i+2). So total required actions in worst case is i+1+N-(i+2) = N-1.
Similarly if we first joined with odd number of 111, let's say position of zero after it is i, then number of actions required to fill at most i/2 — 1 actions, and also we need to make i zeroes, and afterwards remaining length with first zero is N-i, so in worst case we have i/2 — 1 + i/2 + N-i = N — 1.
The only thing left: why we definitely find position with 101, or join with odd? Well, if we don't find, then all segments of 0000 were even, and all 1111 afterwards were also even, this means that total parity was odd. But odd parity can't be translated into even parity, as noted earlier. Or, we can't join odd number of 1111 because they're in the end of array. But then, every segment of 0 is even, so we never may have 101->000 so parity of all segments will be same, they only can disappear, but segment in the beginning and in the ending will remain.
Using segments, ugly code:129203831 Clean python code:129445256
1572C - Покраска
What actions feel dumb?
Paint when borders of same color don't change. 112233->114433
Do we really need to paint blocks without change of borders?
No. And it's not easy to prove. During contest you didn't have to prove it, you might assume it and try to solve without proof.
Try to prove it.
Let's imagine colored tape. Over initial array we will tape segments of same color, so 112233 would become three segments of tape. Next, each action we apply, we instead tape new layer with new color of new segment. For example, 112233->114433 would become four segments of tape: three initial segments plus segment over 22 with color 44, making there 2 layers. Similarly, 112233->112222 is three initial segments plus one segment over whole 2222.
Next, we would like to consider some sequence of actions with paint of segments that doesn't change it's borders. Then we would like to find some bad action then either don't do it, or move it. Here is counterexample of "don't do it" case: 123->124->154->155->111. If we skip 154->155 step, then we can't 154 make into 111 in single step. If we skip 124->154, then we can't get 155 from 124 in single step. This example show how skip of single step may break sequence of steps. If we think, that we can find out what steps we should skip, consider following case:
You can see that first time first element change border is when it has color 2, so you may have idea to make it 2 first time we recolor it. It happens first at 13??->23??. And this is what we want. Then just don't recolor it into 4 and 3 and we indeed have less number of actions. Also you may see that first time when second element change borders is when it has color 1. So, in first time we paint it we would have idea to paint it into color 1 straight ahead. It happens at step 12??->13??, so, we have idea to make it 12??->11?? instead. But then, whole sequence of actions become broken, because we have different borders.
Also, we failed to avoid paint without change of borders. The only easy skippable is something like 12->14->11. We can just make 12->11. But to transform sequence into this case, we probably want to reorder actions.
It's easy to see that for each segment of tape, there are other segments of tape within, and none of them intersecting. And then, very easy to claim that actions within two non-overlapping segments are interchangeable. But they're not, at least in the meaning I want. Here is counterexample:
Consider state before last action: 4111. There are two segments. Let's try interchange actions within them: 3421 apply first action of segment 4 (we did color 3 into 4). 3421->4421 we now have new tape 4, which wasn't in previous set of actions. Also, borders of color change did change in different order. You can't simply claim that if you continue actions you'll get same result. At least you should define what means to continue actions if configuration of segments now different.
So, main issue in this approach is that after we swap actions or change color of segment, it may unintentionally join with other segment during steps in between, and ruin our proof.
Suitable proof is following. Let's say paint action is bad if it doesn't change segment borders. Let's prove that for minimum number of actions there is exists sequence without bad actions. We will prove it by induction by minimum number of steps required.
Base case: minimum steps required = 0. Obviously we don't need bad actions. Induction: minimum steps required is n. Pick this sequence of actions which require n steps. Perform first action. Now we left with n-1 actions, and we know sequence of actions. This means array after performing single action is possible to transform in single color using n-1 actions. Thus, minimum steps required for it is <= n-1. By induction there is sequence of actions with length <= n-1 without bad actions. Either it's exactly n-1 -> and we can just perform first action + n — 1 = n actions. Or there is < n-1 actions, and with our first step is less than n actions in total, which is contradiction with claim that minimum actions required is n. Now, consider our new sequence of actions: first original step plus sequence of n-1 actions without bad actions. This means, that only first action can be bad. If it's not, then we have required sequence of actions. If it's bad, then we have to show how to make it good.
What means that first action is bad? This means, that we paint one of initial segments into different color. Let's say it initially has borders [l, r] and color c, and we paint it with color d. It can't be whole array because n would be zero. So there should exist some step i which is first join of segment [l, r] with other segment and become segment [L, R] with color C.
Now, let's do sequence of actions without first action. Only n-1 actions, up to first point when [l, r] is joined with other segment. Let's say it's action j of n actions. It may surprisingly happen, that j == i. This means, that everything up to i-th action didn't touch segment [l, r] and it still has color c. Also, C != c because otherwise they already would join. This means, that we can color c into C, and continue making actions from step i+1 until end. So we have sequence of n-1 actions which can transform array into single color. But this is contradiction that n is minimum required number of actions.
Other case: j < i. Now, recolor [l,r] into d right before step j. If segment [l, r] doesn't expand by it, then we can continue our sequence of actions, and we will get n actions in total. But if j > 2, we made our bad action second action in sequence of later, so we can replace sequence of actions starting from second step into sequence without bad action using induction hypothesis. Otherwise j = 2, so our sequence looks like: color [l, r] into d, then color something into c, such that if [l,r] would be still c, then it would join to other segment:
But don't forget that only first move is bad, so this can't be the case:
And... You know, this drives me crazy. I spent many hours trying to prove it, and, you can't just say well, every left border in version of first sequence at each step will be less or equal to same border without skipped step 1, also every right border in second sequence at each step will be greater or equal than in version without skip, thus at last step left border will be 0 because in version without skip it was 0, and similarly right border will be n, thus whole segment will be same color. Because: why the hell it should be true? What is the reason? It might be even wrong, but I don't think I can produce counterexample. Also, why wouldn't this colored transition not cause any issues like blocking filling with color that can't pass this one?
So here is example of this case:
After first step, everything is optimal, and no bad moves. And yes, you can paint it faster:
So... NO, I Don't have a proof. I tried everything. I even tried to draw connection with problem from USACO mentioned above, and everything there is much easier.
You can look back-wise and shrink every paint-segment such that each cell which is not covered by newer paint will be inside. Then, expand each paint-segment to make it contain everything it overlaps. Then remove duplicates. And you get nice and pretty nested tree. Last you need to make it binary.
Well, let's continue without proof. I'm sorry. I said I'll give proofs, but well... I'm looking for one though. (even starting to doubt that solution is legit)
What will be if each paint of block change it borders?
It will expand either to the left, or to the right, or in both directions. It also can be represented as a tree. Either two blocks combine, or three blocks combine.
What will be with colors?
It's one of colors of combined blocks. Thus, it's one colors of child node. Color of this child is also color of some child, to the leaf. So color of block is one among initial colors within segment.
How to solve problem without time constraint but it would work, if you need to build tree of segments paint?
Dynamic programming on sub-intervals.
dp[l][r][c] = will tell us how many steps we need to color interval [l, r] into color c. We need to try all possible i between, and try join [l,i],[i+1,j] with all suitable color combination. Also, we need to try to join three segments like when aba -> aaa happens. Time complexity: $$$O(n^3*(n^2+n^3))$$$ Here: $$$n^3$$$ values to compute. Each value computation: ab->aa in $$$n^2$$$ = each color + each place of separation. And aba->aaa in $$$n^3$$$ = each color in the middle + two places of separation.
We didn't prove that we can combine operations within subintervals. How can we make sure that no paint will overflow out of bounds of subintervals? I don't know. Bad news. Probably we can't. But... well, we hope that optimal answer doesn't overflow outside of subintervals. Another proof / thoughts wanted.
Fun fact: if we know how to paint array in minimum steps, then we know how to paint array in any other color with additional step :b
Fun fact 2: there are many colors in which you can paint array in minimum steps.
How to speedup our DP? When we have interval of distinct colors we can color it optimally into any of them, why not pick particular one? Suppose there are several actions of type ab->aa or ab->bb. How can we rearrange? (it's just intuition, very hard to prove)
Intuition tells us, that each time we make ab->aa whole segment has leftmost color. And, each time we make ab->bb it has also rightmost color. And when we do aba->aaa we also has either leftmost or rightmost color. So idea is following, make dp1[l][r] — if we paint subinterval into leftmost color, and dp2[l][r] if we paint subinterval into rightmost color.
I don't dig into details why it works. This time, complexity is: $$$O(n^2 * (n+n^2))$$$, because we totally reduced colors iteration.
Why the hell previous approach works?
Brand new look!
Consider function F that takes array and remove consecutive duplicates, for example F(1,1,2,1,1,3,3,3) = 1,2,1,3. What happens with F(our array) after each operation?
So, operation aba->aaa corresponds to aba->a. And also operation ab->bb corresponds to ab->b. In other words, single operation is deletion of single element, and also new consecutive duplicate if it appeared. And we need to make single element in the end.
Can we update our DP approach using this Brand new look?
Of course we can! Now let dp[l][r] to be minimum required steps to delete everything within [l,r]. But time complexity is still $$$O(n^4)$$$? Because we still need two separations for case aba? Wrong! If aba in the middle, then it looks like ???aba???, but we know that aba will vanish at once, and then one of sides eventually deleted first. So we just need to try each separation in between: [l,i]+[i+1,r]. But there is also case when we delete whole middle: a?????a — we delete all question marks. So there is also case when we need to check dp[l+1][j-1]+1. Will it work? Is it enough? Well, probably something is missing in my description here, but I claim this can be done in $$$O(n^3)$$$ this time.
Take idea with order of vanishing elements within subinterval to the extreme!
Within subinterval [l, r] there is first time when element at position r will vanish. And, at that point in time there will be subinterval [i, r] of vanished elements. Those [i, r] were deleted in fewest steps, otherwise we could reduce number of steps. Also, as I said, in previous step, element at position r was existing. So, there are two possible cases:
This leads to solution.
Remove all consecutive duplicates in initial array. Then, using info from last hint, we will make dp[l][r] — how many steps we need to delete all elements within range [l, r]. Then answer is dp[0][n-1]-1 in zero-based indexing. Just delete whole array minus one step.
129327772
1572D - Бридж-клуб
Notice, there is all possible variants of bits.
Two binary numbers are connected if and only if their binary representation differs at single bit. So there are n coming out from vertex. $$$n\cdot 2^n$$$ edges.
What is asked is very similar to maximum matching, but with exact size of matching. Is there general Matching algorithm?
There is. But it's ridiculously hard. So, this should be some particular graph.
How graph looks when n = 3?
It's cube!
How graph looks when n = 4?
It's four dimensional cube!
Am I dreaming? Is n-dimensional cube is bipartite? No Way! It can't be! (kidding).
Let's put in first partition all vertices with even number of ones in binary representation. And in other partition everything else. It's obvious, that each edge is between partitions.
Btw always look for bipartite graph if you think it should be solved by Matching.
So what?
There is maximum weighted matching algorithm that find out maximum matching increasing it's size from 0 to maximum step by step, and each matching in between has maximum weight. To do that, you need to find out increasing alternating path with maximum impact (additional weight). If you think carefully, it means that first + last vertex of it should have maximum weight.
How to find this path?
You can either use Dijkstra algorithm modified to work as Kuhn, such that each path would cost depending on first vertex and last vertex. Or as I did: sort vertices in partition where I start Kuhn in decreasing order, and then any not-visited vertex is marked as visited and reachable with cost of starting vertex. Then, from each of those we look for best suitable last vertex of alternating path. Then increase cost of matching and switch alternating path. Continue. Each search of new path takes O(V + E), in our case time complexity is $$$O(k\cdot(n + n\cdot 2^n))$$$. Which is too slow.
There is too many edges, and too many vertices. Perhaps some of them are redundant?
How bad should be pair, to be able to replace it with other pair?
Rank of pair is determined by its position in sorted list of all possible pairs. So pair can be replaced with better one, if there is pair above with both unused candidates, or one unused and one from pair we want to replace.
Consider only those pairs with used candidates. What maximum number of them could be? Let's calculate upper bound.
Each possible pair of candidates has n edges coming from first candidate, and n edges coming from second candidate. And single edge is shared by this pair, 2n-1 edges. All those edges we can't use. Suppose in worst case all edges discarded by all pairs are different. So there are k pairs and we each discard 2n-1 edges, k*(2n-1) in total. Thus, if for our pair there are also k*(2n-1)+1 pairs above it, then there is at least 1 free pair with better rank, so we can switch our pair to those. So, we need to consider only k*(2n-1)+1 edges, which is O(n*k) edges, and they use O(n*k) vertices. And our algorithm for finding alternating path will work again in O(V + E), and in this case it's just O(n*k). And time complexity of search of matching becomes O(k*n*k). But there we also need to get first O(n*k) edges. We can't use sort because it would work in $$$O(n^2 \cdot 2^n)$$$ which is slow.
How to get smallest K elements from list of N elements faster than sort (faster than O(N log N))?
There are following approaches:
Using info from Hint 10 we can take only k*(2n-1)+1 edges, and corresponding vertices. To take them, use any approach to take biggest K elements from array. Time complexity: $$$O(n\cdot 2^n + k^2 n)$$$ 129433355
How is the time complexity of the first approach of 1572 — A Book O(nlogn) ? Please can someone explain.
all chapters(n) are once added to set(logn) and removed from it(logn).
so total O(nlogn + nlogn) = O(nlogn)
Thanks a lot.
no problem!
Just to confirm, logn because we are using sortedset? I tried to find some submission which has implemented the first approach but couldn't so not sure.
yes logn because of using sorted set
My Submission
Edit: this has been resolved
Here I'm getting wrong answer on test 2, its failing in conditions like 1 5 0 2 1 3 1 1 4 1 2 3 5 3 1 2 3 required answer 3 my answer 2
If any of y'all are able to find out why my code is failing, do lemme know! thanks!