Hello everyone!
T1duS, Ashishgup,xennygrimmato and I will be capturing the live updates of the Gwalior-Pune 2020 Regionals, for teams to later refer to first-solves and the state of ranklist after various times. It is inspired by similar blogs in the past, like this, for example.
Important Information:
- Rank List (Scoreboard): https://codedrills.io/contests/icpc-gwalior-pune-2020-regional-round/scoreboard
- Contest Page: https://codedrills.io/contests/icpc-gwalior-pune-2020-regional-round
- Contest Blog: https://codeforces.me/blog/entry/93980
- Contest Duration: 4 hours.
- Tentative Start Time: 18:00 IST
Announcements:
- All problems have a memory limit of 1GB, and solutions that exceed this would be marked as RTE instead of MLE due to some memory usage issues.
Live Updates:
- 6.06pm: Treap Trilogy from BITS-Pilani, Goa Campus gets the first AC of the contest on the problem Jeff
- 6.15pm: Jeff is now solved by 112 teams,Vichitrödinger's Cat by 13 teams and Apple Uniformity by 9 teams.
- 6.23pm: Problem A gets its first AC
- 6.27pm: Hold right there Sparky!! from IIT Roorkee is the first team to solve 4 problems.
- 6.29pm: Sheesh! from IIT Jodhpur gets 2 ACs within 30 seconds to lead the scoreboard!
- 6.40pm: Cheese_Maggi from IIT Guwahati gets first AC on Dimitrescu
- 6.51pm: 473 teams have now solved at least 1 problem in the contest.
- 7.03pm: Cheese_Maggi from IIT Guwahati Takes the lead by solving 5 problems.
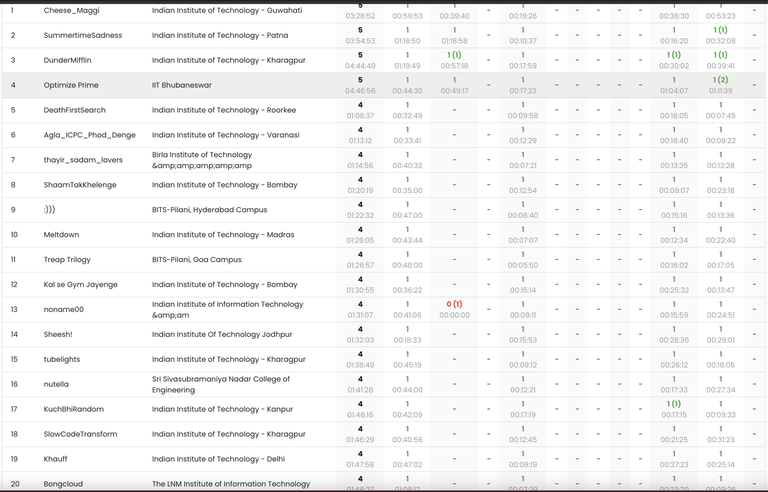
Ranklist at 7:23 PM IST
- 7.35pm : The top 9 teams have solved 5 problems each. The top 2 teams are separated by 8 minutes of time penalty.
- 7.38pm: Cheese_Maggi solve their 6th problem and move up to the top of the scoreboard.
- 7.58pm: Cheese_Maggi still lead, followed by 23 teams with 5 problems solved.
- 8.24pm: Evil Geniuses from IIT Madras move up to Rank #2 after solving Fermod. Cheese_Maggi continue to lead with a 90-minute time-penalty lead.
- 8.40pm KuchBhiRandom from IIT Kanpur also solve their 6th problem
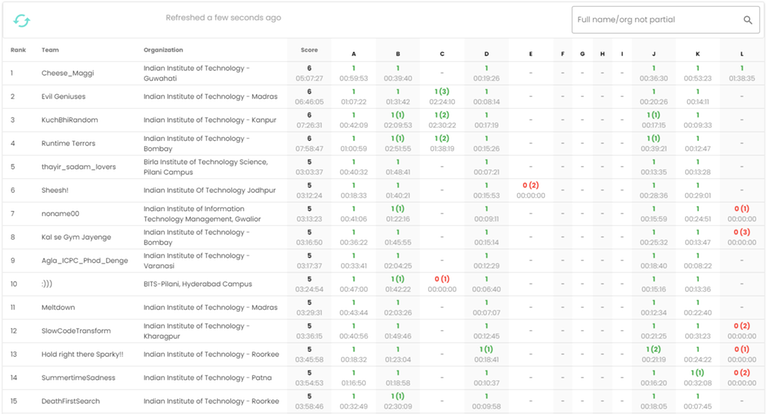
- 9.00pm Scoreboard has freezed
Ranklist at 8.58 PM IST










ICPC Amritapuri 2020 Gwalior-Pune — Live Updates .... ok
It even had a problem with 'Amrita University' in it. :-|
My comment was in reference to the original name of this blog post, haha.
I know, I was pointing to the irony.
Fix the scoreboard
If you say so..
Seems that some college names are clipped? IIIT-Hyderabad is appearing as just "International Institute of Information Technology". Also, can use this userscript to fix the amp issue on frontend temporarily: https://gist.github.com/GaurangTandon/1002be83974e3702605d9334668670d6
Will be fixed after contest.
Fixed at the frontend now.
Dimitrescu was tricky to implement .
Was there any case for no? We could not find any.
There's no case for no.
We were unable to find the exact solution for it till end , some test cases were still getting Wrong. I think that there is a cleaner way of implementing it. what path did you adopt?
We solved individually for each row. For the row with a star, you can break it into left and right parts. If both of them are of length != 1, you can solve them separately in the same way as you do for other rows. If one of them is of length 1, you can put a vertical 1x2 tile on that side and solve the remaining part of the two rows normally. If both of them are of length 1, you can transpose the matrix and do the same thing.
What is the solution for Problem A, Buy N Large?
Consider connected components of the graph formed by the initial associations.
Lets consider the $$$\lfloor \frac{n}{2}\rfloor$$$ cheapest nodes of a given connected component to be coloured black, and the others coloured white.
Clearly there always exists an edge between some black and white nodes, otherwise the component wouldn't be connected.
Also after performing an operation on the nodes connected by this edge, the nodes are removed, but the component remains connected, so the previous logic still holds.
In the case of odd sized components, we can just remove the median value (the smallest white coloured node) on its own, which will leave the graph connected allowing us to use the previously discussed logic.
So we can always use the $$$\lfloor \frac{n}{2}\rfloor$$$ cheapest nodes of a given connected component to eliminate the $$$\lfloor \frac{n}{2}\rfloor$$$ costliest nodes.
I'm still confused why the problem had $$$n \leq 1500$$$
We couldn't come up with this proof and decided to submit and check if it works. It worked. :P Also that n<=1500 constraint somehow forced us to think if the intended solution is dp and not greedy. :P
If that constraint was n<=1e5, pretty sure it will rule out dp approach and teams would have directly thought greedily on this one.
Problem L Neelu in Wanderland, could it be solved using FFT?
We got TLE with NTT, though FFT is faster so maybe it might pass? We didn't end up trying it though.
I managed to solve it with knapsack after a few TLEs. For details, refer to problem G2 of the codeforces Raif round.
We got TLE using a (hopefully) fairly fast FFT implementation, too
FFT is not required.
Since polynomial can be converted to this form :
(1 + x^k + x^2k + ... + x^mk)
We can find resultant polynomial in O(n) using prefix sums taken at k distances.
Basically, we have one range [l,r] which we can easily get. Apart from it we have for i = 1..6 k moves being -i/+i
We can break down down these k moves into log(k) moves by using this trick:
Say for example, you have 50 moves with values +-6.
You can break this into the following moves, +-6*1,+-6*2,+-6*4,+-6*8,+-6*16,+-6*19
This will ensure all cases are covered.
So in total we'll have at max 6*log(n) moves of the kinds +x/-x One move can be merged with the original [l,r] range using bitset. Complexity = 6n*(6*log(n))/64 ~ nlogn
Final Ranklist Plox!!!
Please T1duS BlessRNG
Can anyone help me with the approach of J problem apple uniformity?
Hint: The optimal answer will come from subsegment of length 2
For a given $$$l$$$, $$$r = l + 1$$$ is always the best possible choice. This can be easily proved by analyzing all possible options of the $$$r = l + 2$$$ case.
If $$$a_{l + 2} \leq min(a_l, a_{l + 1}) \leq max(a_l, a_{l + 1}) $$$ — $$$answer= max(a_l, a_{l + 1}) - a_{l + 2} \geq max(a_l, a_{l + 1}) - min(a_l, a_{l + 1})$$$
If $$$min(a_l, a_{l + 1}) \leq a_{l + 2} \leq max(a_l, a_{l + 1})$$$ — $$$answer=max(a_l, a_{l + 1}) - min(a_l, a_{l + 1})$$$
If $$$min(a_l, a_{l + 1}) \leq max(a_l, a_{l + 1}) \leq a_{l + 2} $$$ — $$$answer= a_{l + 2} - min(a_l, a_{l + 1}) \geq max(a_l, a_{l + 1}) - min(a_l, a_{l + 1})$$$
So in all cases, the answer is no better than the answer of just taking $$$r = l + 1$$$.
Now when we update the power of a position $$$x$$$, the only two subarrays which change are $$$[x-1, x]$$$ and $$$[x, x + 1]$$$, so we can just remove the old values for these subarrays and add the new values.
So we want to perform the following operations quickly:
Insert an element
Remove an element
Find minimum element
A multiset can do all these operations in $$$O(log n)$$$.
How did anyone solve problem C: Fermod? We had an answer for all odd M but thats it :/
Could you please tell how did you get the answer for odd M?
Solve for $$$m<=6$$$ by hand. So now take $$$m>6$$$, and let $$$p$$$ be the smallest prime factor of $$$m$$$.
First suppose $$$p \neq m$$$. Then consider the quadruple -
$$$(x,y,z,n)=(m/p,3,m/p+3,p) \text{ if } p>2$$$
$$$(x,y,z,n)=(m/2,3,m/2+3,4) \text{ if } p=2$$$
To show this works, use the fact that $$$p \mid \binom{p}{i}$$$ for all $$$i \in {1,2,\dots, p-1}$$$.
Else if $$$m=p$$$, then take $$$n=p-2$$$, and notice that $$$x^{p-2} \equiv x^{-1} \pmod{p}$$$. So take the three cases $$$(x,y)=(3,3),$$$ $$$(3,4),$$$ $$$(4,4),$$$ and find $$$z \equiv (x^{-1}+y^{-1})^{-1} \pmod{p}$$$ for all three possibilities. It's easy to see that these three values will be different, and so one of them will be $$$>2$$$. Take the corresponding $$$(x,y,z)$$$.
Is there any other solution to this problem?
This is what we did -
We wrote an offline brute force and it was pretty fast for the first 1e6 values.
$$$m=4$$$ is the only impossible case.
For most cases, one of the numbers was $$$3,5$$$. So we took $$$x=3,4,5,7,11$$$.
We hardcoded the first 30 values.
For other $$$m$$$, we had 2 different cases.
If $$$m$$$ isn't prime then $$$n=phi(m)+1$$$ is less than $$$m$$$
Euler's theorem $$$x^n \equiv x$$$ mod $$$m$$$
So we ran a for loop for y from 2 to m-1 and tried all values of x among $$$3,4,5,7,11$$$ until we found one.
For $$$m$$$ being prime,
$$$p=m-1$$$ Lets chose some $$$n$$$,$$$a$$$ and $$$b$$$ let $$$t = n^{-1}$$$ mod $$$p$$$.
We chose $$$x=a^t$$$ , $$$y=b^t$$$ and $$$z=(a+b)^t$$$ $$$x^n = (a^t)^n = a^{(t*n)} = a^{1 mod p} = a$$$ To bypass $$$2 \lt x,y,z,n \lt m$$$ restriction we just randomly chose $$$n,a,b$$$ until we found one which satisfied those requirements.
Initially we took $$$x=3,5,7,11$$$ it was insufficient for $$$m=2^k$$$ we just added $$$x=4$$$ so that $$$x^n$$$ is $$$0$$$ for this mod.
If bruteforce worked pretty fast, means values were pretty small, why didn't you just do that ?
For x,y,z choose first 10 and last 10 numbers. For n choose all numbers as above plus the numbers around phi(m).
I just tried it and it passed.
Here's a much simpler solution:
Can anyone provide me hint for the problem "House Hunting". I thought if we have to select K nodes from the tree so we should start from the bottom like filling the leaf nodes first and then moving to the level above until we select K nodes completely?. Am I correct?
I had an idea during the contest to iterate on the center of the subtree(of k nodes). I think this can be implemented by binary search + centroid decomposition(to check the number of nodes further than a distance x from the center), but not sure as I had not figured out all the details
I tried a similar solution and used segment tree for storing number of nodes at a particular distance from centroid to apply binary search but later figured out few cases were answer will be lower than my answer, I am not sure that such solution will work or not.
I think it will work. When binary searching, if length is odd, keep edge as center else keep node as a center.
To handle edges, just make another tree of n-1 nodes from edges.
Yes, this is the intended solution.
Bonus: Solve it in $$$O(n \log n)$$$
Find a random permutation of the n nodes. Before applying binary search on a particular node, check if the answer found earlier satisfies this node, or else skip that node. So we shall only apply binary search on approximately log n nodes. The resultant complexity would be nlogn.
Solve for $$$ m\leq 6$$$. Now for $$$m > 6$$$,
Both the results can be easily proved.
Edit : Only 2nd is enough, that is $$$(m - 2, m - 2, m - 4, \phi(m) + 1)$$$. The first one can be used for $$$m = 5$$$.
For generating x,y,z:
Non square-free numbers is easy.
Handle divisible by 3,5 cases separately
Fror the rest of the cases, consider any prime divisor p1 and the smallest prime divisor of (p1+1) = p2
$$$x = 3^{p2},y = 4^{p2},z = 5^{p2}, n = (p1+1)/p_2$$$
After generating (x,y,z) I just multiplied it with random numbers till we get a valid triplet.
Will there be an official editorial / discussion session? Also, it would be great if some experienced coders could rate the difficulty level of the problems in terms of CF rating. Thanks.
Discussion session will be on 23rd. More details will be shared soon.
Are we getting T-shirts and goodies this year?
Problem Discussion Session is on Today 23rd Aug, 6 PM IST. Join us here.
Deleted