Добрый день.
Напоминаю, что в воскресенье состоится интернет-версия соревнования 2013-2014 ACM-ICPC, NEERC, Южный четвертьфинал. Начало в 11:00.
Соревнование состоится в разделе Тренировки. К участию приглашаются в большей степени команды — ведь контест подготавливался именно как командное соревнование.
Приглашаю к участию — уверен, это отличный способ потренироваться к четвертьфиналу и/или полуфиналу.











Will this be the same as today's Timus?
Nope. On Timus was the quarterfinal of Eastern subregional of NEERC. Tomorrow will be the quarterfinal of South subregional of NEERC
No. They do other Subregional Contest.
А почему длительность 5:15?
Оказался неприятный момент с тем, что хранилищу задач для тренировок для работы нужен Codeforces, а Codeforces нужно это хранилище (если есть активность в тренировках). Из-за этих технических проблем на старте продлили контест.
И еще: кажется, на что-то смахивает: /contest/67/problem/A
Собственно, вот:
/gym/100253/submission/4911519
/contest/67/submission/336132
Feel the difference:
http://www.diffchecker.com/hv1phtqi
Действительно похоже (эту задачу никто из жюри не вспомнил).
Может в жюри возьмете? :)
Напиши мне email или в личку.
How to solve problem B, F, K ?
Problem B: Move the camera lazily to the nearest good position in every step. You can find the nearest good position in each step by doing f.ex. binary search on the array C.
Problem F: You can write the solution of the expected value as such:
where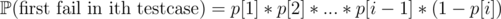 .
.
and t[i] represents the time when i-th testcase will be processed.
Thanks for your reply. I have done the same thing for Problem B. Here is my submission: http://pastie.org/8434448
Getting WA on test #6 , can you tell me why ?
double low = pos[i] — 1.0*r; double hi = pos[i] + 1.0*r;
I think these are incorrect. You should use Pythagoras' theorem here.
r2 = 12 + D2 (where D is the distance you need to add/subtract from pos[i]).
damn !! my code was correct , just that was the issue. :(
Thanks.. :)
can you tell me what kind of test is #6 in B? this is my code. .
l=x[i]-sqrt(ra*ra-1); r=x[i]+sqrt(ra*ra+1);
shouldn't it be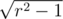 in both cases? :)
in both cases? :)
thanks friend :) accepted
Зачем во всех задачах просить восстановление ответа? У меня в сумме больше часа ушло и еще несколько штрафных попыток, чтобы поприкручивать вывод этого самого ответа к правильным решениям.
Почему на H ловил WA 54??? Что там?
L -- WA 9???
54 типа
4
<<<><<<
Отличный контест, пожалуй лучший из всех Саратовских какие мне доводилось писать. Смутило только 13 задач — слишком много.
А, да: "computer consumes wi watts per hour" — это стыдоба!
А что не так и как правильно?
>ватты в час
Ватты и так в секунду.
А, ну да. Я исходил из формулы W = V·A. Правда, это не отменяет того, что потреблённая мощность измеряется всё-таки в КВт * Ч, а не в КВт/Ч.
представляю себе страшное устройство, которое потребляет мощность...
It's interesting in problem L that : It is guaranteed that there will be no over ow of the 32-bit signed integer type, so feel free to use type int (in C++ or Java) to store the number of dollars and shares.
but I use "int64" got ac ,"int" got WA...
Is it a evil trick?
I used int ( 32 bit signed) got AC. Maybe you have other problem.
Got same issue as you. Just changed my variables to long and got AC. Bizarre o_O
If it helps :
if(d - (inc * a) * p[i] >= 0){This is the line where the overflow is happening for you, looks like for the test case 17(first one, at least), inc * a * p[i] is out of int range. I think most people have written the check
if(d/p[i] - inc * a >= 0 ) {Got it,Thanks for the reply
А здесь нельзя, как на обычных, кодферсовских контестах посмотреть, на каком тесте падает задача. Или посмотреть задачу другого участника.
В тренировках нельзя.
На разборе онсайта кажется СГАУ1 спрашивали про простую идею решения С: построить классы эквивалентности по относительной площади эллипса к фигурам в нем. Проверил сабмитом, единственно не сразу угадал константу точности. Вопрос к ребятам, если прочитают этот пост: на онсайте не сдали из-за того, что заметили только потом? Просто на разборе показалось что это идея не только что пришедшая была. PS: несколько строк неаккуратного кода: 4913039, На пастбине.
Был бы я участником, на 10й минуте бы сдали! :)
Там проблемы с точностью можно убрать, т.к. известно, что площадь параллелограмма с вершинами в целочисленных координатах целочисленная (см. векторное произведение).
Я не пойму, там можно доказать, что даблов хватает, или это просто тесты такие? Я уже понял, что заходило все, даже решения с поворотами плоскости на угол синусами-косинусами. Но почему? Ведь интуитивно кажется, что можно построить ну оооочень близкие по площади фигуры. Уже длина каждого из входных отрезков может отличаться на
10^-16, отсюда площади элипсов — на10^-32. Так как проверке на эквивалентность элипса А и элипса В нам надо сравнивать произведения площади элипса на площадь четырехугольников в нем, то это уже вроде как10^-64.P.S. Я вот честно допишу решение в интах) Только длинку еще надо, так как печаль в том, что (площадь от координат) mod X не равна (площадь от (координат mod X)).
P.P.S. А, ну да, начальные точки целочисельные были, понятно. Тогда халява)
Разумеется, без PPS печаль бы была с точностью, рациональные дроби в длинке.
Там вообще печаль. Она, по ходу, неразрешима в интах.
У меня WA7. Вероятно, там еще много багов, но идею я уже понял.
Входные данные ведь никогда не будут точными, из-за особенностей тригонометрических функций)) Если я хочу сравнивать S1/(a1*b1) и S2/(a2*b2), где S1,S2 — площади четырехугольников, a1,b1,a2,b2 — длины полуосей элипсов, то мне для работы в целых числах надо поднести это в квадрат. Дальше все просто. Для целочисельных координат квадрат длины отрезка в целых мы искать умеем, площадь в целых тоже. Чтобы площадь была действительно в целых, будем брать удвоенную) Если еще и использовать хак "будем сравнивать не числа, а числа по модулю", то можно считать все mod 10^9+7 и вообще не надо длинки. Но вся проблема в том, что я считаю входные данные точными, т.е. считаю корректным умножение на 10^8 и переход к интам. А на самом деле они округлены — если мы поворачивали круг так, что надо умножать на что-то иррациональное, то у нас уже неточный инпут.
Там абсолютно точное решение наверное фейлить будет из-за округления до инпута. (Вообще, обожаю холивары на эту тему, так ведь нельзя задачи делать! :) )
Так как ее сдавать в итоге? В BigDecimal WA7. В double тоже WA7-WA8. Я пытаюсь сравнивать отношения площадей.
Там можно просто сделать в double все, а потом найти ближайшую дробь со знаменателем 100^2.
а) Если везде забить на пи, то классы эквивалентности не изменятся. б) Отношения площадей -- дроби зо знаменателем 100^2.
Немного не понял: Толку от целочисленности площади исходных. Там же после преобразований координаты произвольные. Авторское решение было обратные преобразования и возврат к точным. А на деле можно сравнивать просто относительные площади, а вот как тут с точностью поступить я не вижу. Хотя бы потому, что относительная будет считаться от площади эллипса — иррационального числа.
Целочисленность координат как раз важна. Пусть площадь фигуры во входных данных X. Но мы знаем, что она получена из фигуры площадью 1002π. Найдем это отношение: и умножим на ratio площадь прямоугольников фигурки (это будет площадь прямоугольников в исходной фигуре до преобразований). Тогда мы должны получить целое число. А уже целые числа легко сравнивать между собой.
и умножим на ratio площадь прямоугольников фигурки (это будет площадь прямоугольников в исходной фигуре до преобразований). Тогда мы должны получить целое число. А уже целые числа легко сравнивать между собой.
Да, действительно, торможу. И условие чутка подзабыл. Получается правильнее строить классы эквивалентности не по относительной площади (отношение площади эллипса к площади фигур в нем), а площадь модифицированных домножить на вышеупомянутый коэффициент и спокойно округлить до целого
Как решалась К?
Жадно набираем префикс, который можно обработать одной бригадой. Потом откидываем его и то же самое делаем с оставшимися участками.
А как решались E и J?
E — Посчитаем для каждого солдата количество инверсий, которое он образует. А также общую сумму всех инверсий. Дальше заметим, что при некотором запросе Pi, у всех солдат на суффиксе Pi .. n и IQ <= IQ[Pi], количество инверсий обнуляется и больше никогда не изменяется, а для всех остальных солдат вообще ничего не поменяется. Таким образом, точное расположение солдат после всех этих сортировок нам поддерживать не нужно.
Тогда будем поступать так, заведем дерево отрезков, с поддержанием минимума и его позиции, где значениями будут IQ солдат. На каждом запросе Pi, будем доставать солдата с минимальным IQ на отрезке Pi .. n, и если его IQ <= IQ[Pi] отнимать количество инверсий, которое он образует и удалять его из дерева отрезков, например заменяя его IQ на какое-нибудь большое число. Если при запросе, солдата с номером Pi мы когда-то обрабатывали, то игнорируем этот запрос.
Итого, каждого солдата мы обработаем ровно один раз и сложность получается O(N * logN).
J — Можно заметить тот факт (доказать), что нам выгодно решать задачи по возрастанию времени. Тогда можно построить динамику по состояниям [сколько задач прошли][сколько задач ожидают сабмита][текущее время] = количество очков. Переходы — начать решать задачу или пропустить ее. При первом переходе еще дополнительно переберем сколько задач из тех, которые ожидают сабмита, мы хотим сдать пока решаем текущую задачу, проверять сколько можем решить, можно просто суммой на отрезке времени. Только этот переход нужно реализовать очень аккуратно.
Далее пройдем по финальным состояниям, и если оставшиеся задачи для сабмита мы можем сдать за оставшееся время, то рассматриваем это состояние как вариант для лучшего ответа. Далее получаем список задач, которые мы сдадим и восстанавливаем ответ просто жадно эмулируя процесс сдачи.
Сложность получается что-то типа O(N^3 * 10^4), но заходит быстро, потому что получается много недостижимых состояний.
В J можно написать N*N*N*T, где T — время (10^4), с намного более простыми переходами и меньшим риском багов.
Будем перебирать то, сколько задач мы вообще решим. Если зафиксировать это число, то можно легко определить ограничения на время решения задач — если хотим решить К задач, а моменты наличия интернета отсортированы в массиве X[m], то на решение первой у нас есть X[m-k+1] минут, на решение первых двух — X[m-k+2]-1 минут, и так далее, на решение всех K — X[m]-k+1 минут. Далее обычный рюкзак for for for, с тем отличием, что мы не рассматриваем переходы из невалидных состояний (когда использованное время превышает ограничение для текущего числа задач).
можно за N*N*T
Problem K : Wrong answer on test 9. Any Critical input please !!!
My code for problem H gets WA on testcase #55! Does anybody know that testcase or can spot my mistake? My code
For this case
5 <<<<><<<<you got-1, but the answer should beabcdeabcde.Thanks! Fixed and Accepted:D
11/6 Finally got it. Sort of. It took about 80min to generate the answers for n=6, which I then hardcoded, so I'm wondering what the intended solution was.
============
EDIT: Well, I decided to test more for J, and I see that I clearly get things wrong, time to fix... (4 2 != 2 4)
I seem to be quite hasty in my conclusions.
============
I'm suspicious of the judge for problem J. I get WA on test case 10, and through testing the judge, this is the first case which relies on the modulus. I've changed the modulus and still get AC up to test case 10, so I suspect that the judge code used a different modulus than the problem statement.
Alternatively, it could be some small case that I get wrong regardless, but I've verified that my program correctly solves n=1, for any m, and perhaps also for n=2, any m.
I'm getting WA at test case 32 at problem I. Any help...
Each of a and b can be up to 5000, so you need to double the size of
s. By the way, you’re missing areturnkeyword inoperator <, but you don’t actually need that line anyway.Thanks a lot!!!
Как решать A? У нас ничего умнее динамики за четвертую степень не придумалось
Динамикой за 3-ю степень :) Из-за восстановления ответа получается много кода, но само решение не сложное. вот.
Идея такая. Для каждого типа телешоу посчитаем дополнительную динамику "сколько счастья принесут телешоу i-го типа, если разбить их на j групп" (т.е. будет ровно j телешоу i-го типа, для которых перед ним стоит шоу другого типа).
Как соединять телешоу разного типа? Переберм максимальное количество групп, на которое разбили телешоу некоторого типа (назовем это число Х). Тогда в сумме все другие телешоу должны разбиваться как минимум на Х-1 группу (т.е в сумме все телешоу должны разбиваться не менее чем на 2*X-1 группу). А это уже рюкзак, который работает за O(n^3).
А потом долго и нудно восстанавливаем ответ.
Is there any plan to organize Internet-version NEERC 2013?
It will be published as a training in Gym as soon as jury will publish tests.
Is there any editorial for this contest?