awoo's blog

Educational Codeforces Round 111 Editorial
By awoo, history, 3 years ago, translation, In English

1550A - Find The Array

Idea: BledDest

Tutorial
Solution (BledDest)

1550B - Maximum Cost Deletion

Idea: Neon

Tutorial
Solution (Neon)

1550C - Manhattan Subarrays

Idea: adedalic

Tutorial
Solution (adedalic)

1550D - Excellent Arrays

Idea: adedalic

Tutorial
Solution (adedalic)

1550E - Stringforces

Idea: BledDest

Tutorial
Solution (awoo)

1550F - Jumping Around

Idea: BledDest

Tutorial
Solution 1 (awoo)
Solution 2 (awoo)
  • Vote: I like it
  • +178
  • Vote: I do not like it

Comments Comments (47)
| Write comment?
»
3 years ago, # |
  Vote: I like it +11 Vote: I do not like it

Nice Editorial!

→ Reply
»
3 years ago, # |
  Vote: I like it +13 Vote: I do not like it

Thanks for good Editorial and solutions. Problem C was lovely to thinking on)

→ Reply
»
3 years ago, # |
← Rev. 3   Vote: I like it +17 Vote: I do not like it

Non-graph solution to F:

Since the maximum coordinate is at most $$$10^6$$$, so long as we process each square a small number of times, we're good. Let's say we have a set of all squares that are reachable with some range value $$$k$$$. What new squares will we be able to reach when $$$k$$$->$$$k+1$$$? Those squares which we haven't yet reached, and are neighbors of some square in our set. On top of that, we might reach some rocks, which will be able to reach an interval of squares at distances $$$[d-k,d+k]$$$ from it.

So, let's keep a set of all edge squares — those that are not yet reachable with current value $$$k$$$, but are neighbors of a reachable square. In each step of increasing $$$k$$$, we will process all edge squares, mark them as reachable, and check their two neighbors — at most one of them might be a new edge square. If the edge square is a rock, we add it to our unprocessed rock stack.

Then, process all rocks while we have some left: find all unprocessed squares that are a distance of $$$[d-k, d+k]$$$ from it (if this finds more rocks, add them to the stack). We can do this operation by using a segment tree which keeps track of how many unprocessed squares are in any interval. If we query to process squares in $$$[L,R]$$$, and there are none, we just return, otherwise we recurse into the two subtrees that make it up. Everytime we reach a leaf of the tree, we process the square it represents, and will never visit it again, so across all these rock-queries we will process $$$O(X)$$$ squares each taking $$$O(logX)$$$ time, where X is the size of the coordinates. After we're done with all the rocks, we look at the neighbors of all the new squares we managed to reach, and add new edge squares to our set.

In the end, we process each square a constant number of times, and processing a square takes $$$O(logX)$$$ (getting to its leaf node in the segment tree/adding it to set).

We can either mark for each rock the $$$k$$$ that we needed to reach it and stop when all rocks are marked, or sort queries by their $$$k$$$ and answer them as we increase $$$k$$$, and once all queries are answered, sort them by index and print their answers.

The time complexity is $$$O(n+XlogX+q)$$$.

Submission (sorry for the slight mess, had bugs during contest :) )

→ Reply
»
3 years ago, # |
← Rev. 2   Vote: I like it +4 Vote: I do not like it

this Educational Codeforces Round 111 problems are hard as compare to other Educational Codeforces Rounds.

→ Reply
»
3 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Really Good C Problem

→ Reply
»
3 years ago, # |
  Vote: I like it +12 Vote: I do not like it

Problem C was a good one, learned a new concept through the problem in upsolving.

→ Reply
»
3 years ago, # |
  Vote: I like it +4 Vote: I do not like it

After reading the editorial of D, it doesn't seem even so hard!

→ Reply
»
3 years ago, # |
← Rev. 2   Vote: I like it +20 Vote: I do not like it

There also exist solutions using segment trees and/or divide and conquer for C.

For the first solution, firstly find the next >= and <= element for each element. Now we need to find the closest element on the right which forms a non-increasing or a non-decreasing chain with the current element. If we do this, using a segment tree, we can do a two-pointers solution for greedily choosing the farthest possible end for a good subarray (for each index) using these values. To this end, the divide and conquer works as follows: break the array into two halves, and we will use the elements on the right as candidates for the middle elements for the chains of length 3, and update the closest values for the elements on the left. For achieving this, we can simply run coordinate compression and use prefix/suffix sums to compute the closest possible element which is at least (or at most) x. The time complexity is $$$O(n \log^2 n)$$$. Relevant submission: 122511482.

For the second solution (found by timreizin), we can do a much simpler sweep. For each element, we can use two segment trees (dynamic or with coordinate compression) and store the indices of the closest elements on the left, which are <= and >= the current value respectively. So if we query for the current element before updating it in the segment trees, we'll get at most 2 elements in the chain till just after those elements, and hence we can simply use the closer one to compute the largest subarray ending at the current index. The time complexity is $$$O(n \log n)$$$. Relevant submission: 122514591.

→ Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it +9 Vote: I do not like it

    we can also find the number of bad subarrays and answer = total subarrays — bad subarrays

    to find the number of bad subarrays we can find the left minimum, left maximum, right minimum and right maximum for every ith element, and from this, we can find the range of the bad subarrays by iterating on the array and taking the ith element as the middle element, and then through this range, we can find the number of the bad subarrays starting from the ith element. 122504943

    → Reply
  • »
    »
    3 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    Yes, exactly what I was trying to do in the contest, can you tell me how to find the second next >= and <= for each element in given array. I thought so hard on this, but still could not do it,any help would be appriciated. Therefore I stumbled on a different subproblem, which I mentioned here:https://codeforces.me/blog/entry/92810#comment-816475

    → Reply
    • »
      »
      »
      3 years ago, # ^ |
        Vote: I like it +6 Vote: I do not like it

      I will show how I did it for a >= (<= is the same, with some easy changes). At first for every element find index of the nearest >= on the left. I needed a segment tree(dynamic or usual after compressing coordinates). In this segment tree we store -1 for all elements at the beginning. Then, we will work with our array from 0 to n — 1. After proceeding each index I set value at point a[I] in a segtree to it's "index of the nearest >= on the left". For index i(when we proceed them from 0 to n — 1, in the same cycle with updates to segtree) I take maximum in a range(a[I], maxA). Result of this query will be the needed index.I think this submission will help in understanding. 122484928

      → Reply
    • »
      »
      »
      3 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      The key idea in the first solution is to essentially look at the second element of each chain (which has 3 elements each). And this is what I do in the divide and conquer stage. Basically, you look at all possible chains with the middle element in the right half, and the first element in the left half. All the rest have the first two elements in the same half, and this case is covered by the two recursive calls to the left and the right halves.

      → Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem C, why we can't form a bad triple when i<j<k isn't true?

→ Reply
  • »
    »
    3 years ago, # ^ |
    ← Rev. 3   Vote: I like it +14 Vote: I do not like it

    Because we can — so statement "we can't" is false. It's really obvious — draw them (all 6 variation of < and > for second coords) — it's really easier to see than to write ~10-15 lines of words explaining this variations.

    → Reply
  • »
    »
    3 years ago, # ^ |
    ← Rev. 2   Vote: I like it +1 Vote: I do not like it

    We can if k < j < i, but j needs to be between i and k.

    Consider, for example:

    i < k < j

    Then:

    d(p, r) = |k - i| + |ak - ai| = k - i + |ak - ai|

    d(p, q) + d(q,r) = |j - i| + |aj - ai| + |k - j| + |ak - aj| = j - i + j - k + |aj - ai| + |ak - aj|

    But:

    |aj - ai| + |ak - aj| >= |ak - ai|

    and, since j > k

    j - i + j - k > k - i + k - k = k - i

    so

    d(p, q) + d(q,r) > k - i + |ak - ai| = d(p, r)

    So there can be no bad triple if i < k < j

    Similarly there can be no bad triple for j < i < k, k < i < j, or j < k < i

    → Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    because coordinate of x is i,j,k。if one array is good.These three points is in the same straight line

    → Reply
    • »
      »
      »
      3 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Sorry,it's bad triple not good and they are not must in the same straight.if i<j<k ,(i,k)=hk-hi+k-i;(i,j)= hj-hi+j-i,(j,k)=hk-hj+k-j;(i,j)+(j,k)=hk-hj+hj-hi+k-j+j-i=hk-hi+k-i=(i,k)

      → Reply
»
3 years ago, # |
  Vote: I like it -31 Vote: I do not like it

Video Editorials of this Round A. Find The Array B. Maximum Cost Deletion

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I loved Problem C !

→ Reply
»
3 years ago, # |
  Vote: I like it -15 Vote: I do not like it

ABC-forces

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I have a doubt in problem A

I figured out the solution is ceil(sqrt(n)) pretty fast but was afraid should I submit it or not.

The reason is I faced penalty for using ceil function to round up divided answers. I learnt I should write (a+b-1)/b instead of ceil(a/b) because ceil function has precision errors.

But when I submitted ceil(sqrt(n)), it passed. So, why isn't it showing precision error in that case?

Is the test cases weak, or is there something about ceil function I'm missing ?

→ Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    ceil function in C++ will print the number as it's if the number < $$$10^6$$$ otherwise it'll print it in the form 1e+n (like $$$10^6$$$ it'll printed as 1e+06) but in A the maximum number will be printed is 71 so doubles will work

    PS: that's will not change that (a + b - 1) / b is always better, so try as possible to avoid doubles!

    → Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I didn't get the equations for the solution of problem A. Specially these lines - "Let ⌈s√⌉=d. By taking 1+3+5+7+⋯+2d−3, we achieve a sum of (d−1)2 using d−1 elements. s−(d−1)2 is not less than 1 and not greater than 2d−1 (since (d−1)2−−−−−−−√=d−1, and (d−1)2+2d−−−−−−−−−−−√>d). Thus, we can just add s−(d−1)2 to our array, and the sum becomes exactly s."

    Would you please explain little more or any reference to understand these lines.

    → Reply
    • »
      »
      »
      3 years ago, # ^ |
      ← Rev. 2   Vote: I like it +3 Vote: I do not like it

      Basically if sum is n*n then it answer is n, if sum is less than that of n*n but more than (n-1)*(n-1) the answer is still n as:

      suppose sum is 9 => array is 1 3 5 `suppose sum is not 9 but between 4 and 9 (say 8) => then array is 1 3 4` suppose it is 7 => then array is 1 2 4

      Similarly we can prove that we can make changes to array so that array becomes equal to sum but with same number of elements.

      → Reply
»
3 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

Problem C was actually nice. Actually there is a kinda interesting theorem, that might help in such problems: for every sequence numbers length N the product of the length of LIS(longest increasing subsequence) and LDS(longest decreasing subsequence) is greater than N. For instance, either length of LIS or LDS should be greater than ceil(sqrt(N)).

So if we take a sequence of length 4, that max(length(LIS), length(LDS)) is 2, because sqrt(4) is 2 and this is an integer. But, for length 5, there always would a LIS or LDS of length 3. This is exactly what we had to observe in this particular problem. Hope this little fact might help you in the future

P.S. on russian ITMO-wiki there is a proof of this theorem

→ Reply
»
3 years ago, # |
  Vote: I like it -12 Vote: I do not like it

Solution for A problem without a loop:

def beautiful_array(num):
    square_root = math.sqrt(num)
    if square_root.is_integer():
        return int(square_root)
    else:
        return int(math.floor(square_root) + 1)
→ Reply
  • »
    »
    3 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Is it a bad solution or is it considered bad to publish your own solutions? I don't get it, I am new here.

    → Reply
    • »
      »
      »
      3 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      You have several dropdown options before you comment. The rightmost one is a CF symbol. Click on spoilers and then post your code. Like this

      This is a spoiler.

      As to how to format your code inside the spoiler(or in general). look here

      Or you could post the link to your code.

      → Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem C Manhattan Subarrays
Why does a sequence of length greater than or equal to 5 have a subsequence of length 3 that does not increase or decrease

→ Reply
»
3 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I can't make any sense of the code used to calculate pos[i][j] in problem E

→ Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    I have a simpler implementation imo .you can check it out, to calculate pos[i][j] you iterate backwards while keeping a counter (called cur in the code) for each alphabet meaning what is the longest substring with all letters equal to this alphabet starting from the current position 122726559

    → Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    It represents the minimum position which is free after we have placed a block of length "mid" (from the binary search) after the index i for some particular letter j.

    Now there are two cases---->

    1. Either from i to i + mid there is not a single letter of type other than j or '?'. In this case we can place a block here so update pos[ i][ j] to i+d . To ensure this we move Check once from 0 to i-1 and the next time from (length of array)-1 to i+1.

    2. We have some guy other than our letter j and '?'. Update it to pos[ i+1][ j]

    → Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Regarding Problem C: "The final observation is that any sequence of length at least 5 contains either non-decreasing or non-increasing subsequence of length 3" I think the array 5 8 3 4 2 doesn't contain any sub-array of length 3 which is either non-increasing or non-decreasing. All the sub-arrays of length 3: 5 8 3, 8 3 4 and 3 4 2 are neither non-increasing nor non-decreasing. Problem stated "A subarray of the array a is the array a(l),a(l+1),…,ar for some 1≤l≤r≤n" Am I missing something?

→ Reply
  • »
    »
    3 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I guess, it's a confusion about terminology. The problem statement explains what it means by "good array" and what it means by "subarray". The editorial uses a new word "subsequence", which is not the same as "subarray".

    Your array [5, 8, 3, 4, 2] is not good, because we can choose three distinct indices $$$i=2$$$, $$$j=3$$$, $$$k=5$$$. Points $$$(8, 2)$$$, $$$(3, 3)$$$ and $$$(2, 5)$$$ form a bad triple.

    → Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain to me the solution of Problem B, especially this part — cout << n * a + max(n * b, (m / 2 + 1) * b) << '\n';

→ Reply
  • »
    »
    3 years ago, # ^ |
    ← Rev. 3   Vote: I like it +8 Vote: I do not like it

    You have to delete all the characters in the whole string so the number of points you receive first is a*n. Therefore, you will consider 2 cases:

    Case 1 is b >= 0: you have to maximize the operations (because the more operations you do, the more number of points you will get because b >= 0) so the answer of this case will be n * b.

    Case 2 is b < 0: you have to minimize the operations (because the more operations you do, the less number of points you will get because b < 0).

    I have an example: 10000111100011111.

    You see that the string above has 5 blocks, 2 blocks adjacent has no equal characters and the string consists of just 1s and 0s. You will find out that, instead of delete 5 blocks in 5 operations (1 -> 000 -> 1111 -> 000 -> 11111), we just need to delete the middle blocks (*), the blocks that adjacent to this block will merge into one so that it takes 3 operations (0000 -> 000 -> 1111111111), which is less than 5 operations. If the string has m blocks 0s and 1s, the number of operations (*) is m/2 and 1 operation more to delete the rest characters. Therefore, the answer of this case is m/2 + 1.

    Because you need to find the optimal result of the problem, you will compare m/2 + 1 to n*b to find what is larger, after that plus n*a and print the result.

    (Sorry for my bad english :( hope you will understand.)

    → Reply
»
3 years ago, # |
  Vote: I like it +1 Vote: I do not like it

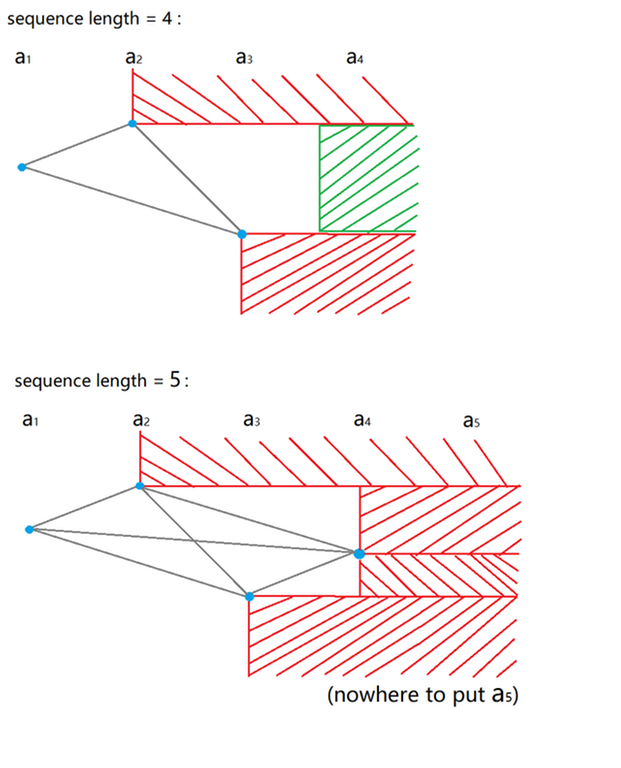
I drew a picture to show that any sequence of length at least 5 contains either non-decreasing or non-increasing subsequence of length 3 in problem C. I hope it helps.
blue point -> value of a[i]
grey line -> possible combination of a[i] and a[j]
red area -> the last number cannot be placed here (otherwise there is bad subsequence)
green area -> the last number can be placed here

→ Reply
»
3 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I can present a more sound proof for C that doesn't use any theorem. First we can prove that for any pair $$$a_1, a_2, a_3$$$, $$$a_1 <= a_2 <= a_3$$$ and $$$a_1 >= a_2 >= a_3$$$ are forbidden because they will result in a bad tripe.

Now after that, for any five consecutive numbers the only "valid" constructions will be $$$a_1 <= a_2 >= a_3 <= a_4 >= a_5$$$ and $$$a_1 >= a_2 <= a_3 >= a_4 <= a_5$$$. I will show that these are not "valid".

In the first case: $$$a_1 <= a_2 >= a_3 <= a_4 >= a_5$$$ Let's observe $$$a_2$$$ and $$$a_4$$$: if $$$a_2 <= a_4$$$, then $$$a_1, a_2, a_4$$$ will be a bad triple, otherwise if $$$a_2 >= a_4$$$, $$$a_2, a_4, a_5$$$ will be a bad triple.

The second case can be proved analogically.

This way we proved that a good subarray will have length smaller or equal to 4.

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

First time seeing Boruvka's Algorithm in use. Nice problems! Especially E and F

→ Reply