Thank you for competing! I hope you had fun in the contest. UPD: Implementations have been added.
103150A - Addition Range Queries
The value of $$$k$$$ is irrelevant, just output the answer when zero operations are performed.
If we perform $$$0$$$ operations on the array, then the answer is just $$$\max{(a_i)} - \min{(a_i)}$$$ (maximum element of $$$a$$$ minus minimum element of $$$a$$$). Call this value $$$r$$$. Now we claim that, no matter how many operations are performed on the array, the answer will always be $$$r$$$. Let's prove it.
Let $$$s$$$ be the sum of the elements of the array. Then the operation is equivalent to turning $$$a_i$$$ into $$$s - a_i$$$ for all $$$i$$$. In particular, let $$$a_p$$$ be the maximum element and $$$a_q$$$ be the minimum element of $$$a$$$. Then after the operation, $$$a_p$$$ becomes $$$s - a_p$$$ and $$$a_q$$$ becomes $$$s - a_q$$$. It's easy to see that $$$s - a_p$$$ will be the smallest number of the resulting array, and $$$s - a_q$$$ will be the largest number of the resulting array. Therefore, after the operation, the maximum difference between two numbers is $$$s - a_q - (s - a_p) = a_p - a_q$$$, which is equal to the answer for the initial array.
Therefore the answer is independent of $$$k$$$. The solution goes as follows: find the minimum and maximum of $$$a$$$, and then find their difference. This runs in $$$\mathcal{O}(n)$$$ per test case.
#include <bits/stdc++.h>
using namespace std;
const int MAX = 200007;
const int MOD = 1000000007;
void solve() {
int n, k;
cin >> n >> k;
int a[n + 7], mn = MOD, mx = -1;
for (int i = 0; i < n; i++) {
cin >> a[i];
mn = min(mn, a[i]);
mx = max(mx, a[i]);
}
cout << mx - mn << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int tt; cin >> tt; for (int i = 1; i <= tt; i++) {solve();}
}
We can solve the one-dimensional version using a DP (or just iterating), so solve the two-dimensional version using by splitting the grid into vertical and horizontal segments that don't interact.
First, let's solve the one-dimensional problem, where the only characters are $$$\texttt{<}$$$ and $$$\texttt{>}$$$. In this case, there is a brute-force solution that swaps two arrows whenever it can, but this runs in $$$\mathcal{O}(n^2)$$$. Unfortunately, I intended to make this fail, but it looks like I didn't. I apologize for this.
To solve this problem in $$$\mathcal{O}(n)$$$, we will use dynamic programming. Let $$$a_i$$$ be the maximum number of swaps that can be performed first $$$i$$$ characters of the string. Let's also keep track of the number of right arrows we've seen so far in a variable $$$rt$$$. Initially $$$a_0 = 0$$$ and $$$rt = 0$$$. Then, iterate through the string from left to right:
If $$$s_i = \texttt{>}$$$, then $$$a_i = a_{i-1}$$$ and $$$rt = rt + 1$$$.
If $$$s_i = \texttt{<}$$$, then $$$a_i = a_{i-1} + rt$$$.
This DP works since each left arrow can move as many times as the number of right arrows it is pointing at.
Now we return to the two-dimensional case. For each square, let's split the grid into multiple components: if the arrow is $$$\texttt{<}$$$ or $$$\texttt{>}$$$, then we will keep moving horizontally until we hit a $$$\texttt{v}$$$ or $$$\texttt{^}$$$ arrow. Similarly, if the arrow is $$$\texttt{v}$$$ or $$$\texttt{^}$$$, then we will keep moving vertically until we hit a $$$\texttt{<}$$$ or $$$\texttt{>}$$$ arrow. This works, because horizontal arrows will never interact with vertical ones, and vertical arrows will never interact with horizontal ones.
For example, the above process results in the following components in the first test case.
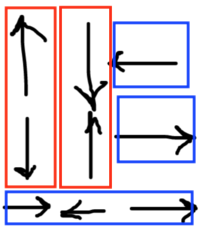
Now we can just solve each component individually, and add the answers. This runs in $$$\mathcal{O}(mn)$$$.
An implementation note: we don't actually need a DP array to solve each component; instead, you can just keep track of two variables $$$ans$$$ and $$$rt$$$.
#include <bits/stdc++.h>
using namespace std;
const int MAX = 200007;
const int MOD = 1000000007;
bool lr(char c) {
return (c == '<' || c == '>');
}
void solve() {
int n, m;
cin >> n >> m;
char c[n + 7][m + 7];
bool vis[n + 7][m + 7];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> c[i][j];
vis[i][j] = false;
}
}
long long res = 0, curr, cnt;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
curr = 0;
cnt = 0;
if (!vis[i][j]) {
int x = i, y = j;
if (lr(c[i][j])) {
while (x < n && y < m && lr(c[x][y])) {
vis[x][y] = true;
if (c[x][y] == '<') {curr += cnt;}
else {cnt++;}
y++;
}
}
else {
while (x < n && y < m && !lr(c[x][y])) {
vis[x][y] = true;
if (c[x][y] == '^') {curr += cnt;}
else {cnt++;}
x++;
}
}
}
res += curr;
}
}
cout << res << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
solve();
}
We can't swap two letters if they are already sorted.
The key insight is this: let $$$c_1$$$ and $$$c_2$$$ be two characters such that $$$c_1$$$ comes before $$$c_2$$$ in the alphabet and $$$c_1$$$ comes before $$$c_2$$$ in the input string $$$s$$$. Then it is impossible to swap $$$c_1$$$ and $$$c_2$$$. We can prove this by noticing that any operation that contains both $$$c_1$$$ and $$$c_2$$$ will never swap them, since $$$c_1 < c_2$$$ and the operation always sorts the substring picked. On the other hand, if two characters are not sorted, then we can sort them easily using the operation.
Let's look at all pairs of characters in $$$\texttt{ezpc}$$$ such that the first is greater than the second. These pairs are $$$(\texttt{e}, \texttt{c})$$$, $$$(\texttt{z}, \texttt{p})$$$, $$$(\texttt{z}, \texttt{c})$$$, $$$(\texttt{p}, \texttt{c})$$$. If any of these pairs are in the wrong order in $$$s$$$, then we will be unable to swap them. This means that the string cannot be easy. On the other hand, if all of these pairs are in the right order, then we can always make the string easy.
Therefore the solution is just to look for the positions of $$$\texttt{e}$$$, $$$\texttt{z}$$$, $$$\texttt{p}$$$, and $$$\texttt{c}$$$ in $$$s$$$, and check if any of the following are true: $$$pos_e > pos_c$$$, $$$pos_z > pos_p$$$, $$$pos_z > pos_c$$$, $$$pos_p > pos_c$$$. If any of them are true, then the answer is $$$\texttt{NO}$$$. Otherwise, the answer is $$$\texttt{YES}$$$. This runs in $$$\mathcal{O}(1)$$$ per test case, since the length of $$$s$$$ is fixed.
#include <bits/stdc++.h>
using namespace std;
const int MAX = 200007;
const int MOD = 1000000007;
void solve() {
string s;
cin >> s;
int epos, zpos, ppos, cpos;
for (int i = 0; i < 26; i++) {
if (s[i] == 'e') {epos = i;}
if (s[i] == 'z') {zpos = i;}
if (s[i] == 'p') {ppos = i;}
if (s[i] == 'c') {cpos = i;}
}
if (cpos < epos || ppos < zpos || cpos < zpos || cpos < ppos) {
cout << "NO" << endl;
}
else {
cout << "YES" << endl;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int tt; cin >> tt; for (int i = 1; i <= tt; i++) {solve();}
}
The maximum distance the center can move is $$$\lfloor \frac{n}{2} \rfloor \sqrt{2}$$$. We can make a construction for this value of $$$d$$$.
First notice that if we have a construction for some $$$d$$$, then we have a construction for all $$$d' < d$$$ (since all points move at least $$$d'$$$).
Notice that maximum distance the center point (or any of the center points, if $$$n$$$ is even) can move in an $$$n \times n$$$ grid is $$$\lfloor \frac{n}{2} \rfloor \sqrt{2}$$$, which can be shown through casework on whether $$$n$$$ is even or odd. Therefore, if $$$d > \lfloor \frac{n}{2} \rfloor^2 \cdot 2$$$, then the answer is $$$\texttt{NO}$$$.
Otherwise, the answer is $$$\texttt{YES}$$$. As mentioned before, we only need to find a construction when each point moves at least $$$\lfloor \frac{n}{2} \rfloor \sqrt{2}$$$ units. If $$$n$$$ is even, we can use the construction below:
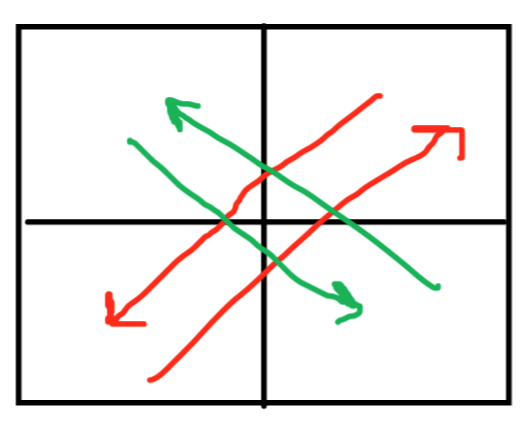
If $$$n$$$ is odd, then we can move all the points in the lower-left $$$(n-1) \times (n-1)$$$ grid as before, and move the remaining points as shown:
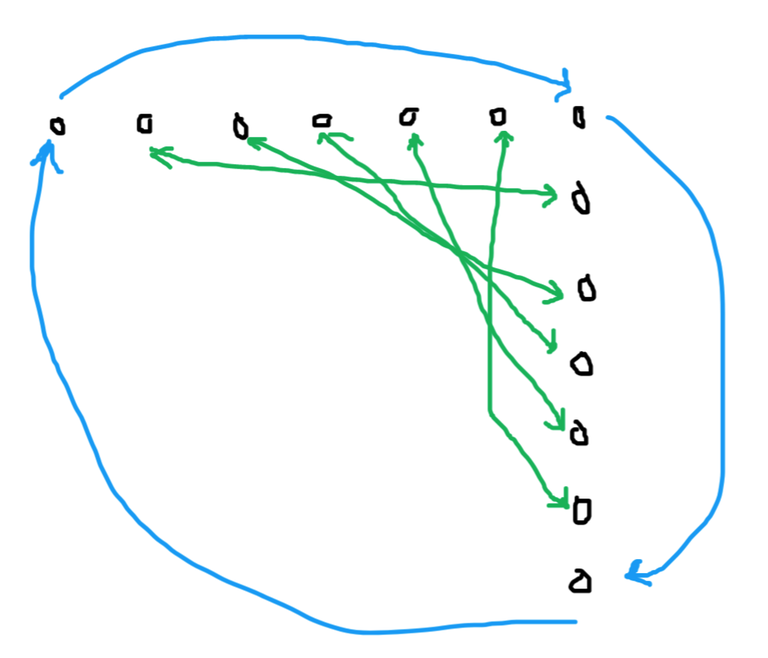
It's easy to see that this will indeed satisfy the conditions. This runs in $$$\mathcal{O}(n^2)$$$ per test case (for output).
#include <bits/stdc++.h>
using namespace std;
const int MAX = 200007;
const int MOD = 1000000007;
void f(int x, int y) {
cout << x << ' ' << y << ' ';
}
void solve() {
int n, d;
cin >> n >> d;
if (d > (n / 2) * (n / 2) * 2) {cout << "NO" << endl; return;}
cout << "YES" << endl;
for (int i = 1; i <= n / 2; i++) {
for (int j = 1; j <= n / 2; j++) {
f(i, j); f(i + n/2, j + n/2); cout << endl;
f(i + n/2, j + n/2); f(i, j); cout << endl;
}
}
for (int i = 1; i <= n / 2; i++) {
for (int j = n / 2 + 1; j <= (n / 2) * 2; j++) {
f(i, j); f(i + n/2, j - n/2); cout << endl;
f(i + n/2, j - n/2); f(i, j); cout << endl;
}
}
if (n % 2) {
f(1, n); f(n, n); cout << endl;
f(n, n); f(n, 1); cout << endl;
f(n, 1); f(1, n); cout << endl;
for (int i = 2; i <= n - 1; i++) {
f(i, n); f(n, n + 1 - i); cout << endl;
f(n, n + 1 - i); f(i, n); cout << endl;
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int tt; cin >> tt; for (int i = 1; i <= tt; i++) {solve();}
}
The answer is $$$\texttt{YES}$$$ if and only if $$$t$$$ contains the character $$$\texttt{o}$$$.
First, if the resulting string $$$t$$$ doesn't have the character $$$\texttt{o}$$$, then the answer is $$$\texttt{NO}$$$, since after every operation the resulting string must have a character equal to $$$\texttt{o}$$$.
Otherwise, we claim the answer is $$$\texttt{YES}$$$. Suppose that $$$t$$$ has a character $$$\texttt{o}$$$ at position $$$i$$$. Then the first operation should make $$$s_i = \texttt{o}$$$ (and change any other character). Afterwards, we can make $$$s_i = \texttt{o}$$$ and, one by one, make all the characters in $$$s$$$ match $$$t$$$. (Formally, make $$$s_i = \texttt{o}$$$ and $$$s_j = t_j$$$ for all $$$1 \leq j \leq n$$$, $$$i \neq j$$$.)
This runs in $$$\mathcal{O}(n)$$$ per test case.
#include <bits/stdc++.h>
using namespace std;
const int MAX = 200007;
const int MOD = 1000000007;
void solve() {
int n;
cin >> n;
string s, t;
cin >> s >> t;
for (char c : t) {
if (c == 'o') {cout << "YES" << endl; return;}
}
cout << "NO" << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int tt; cin >> tt; for (int i = 1; i <= tt; i++) {solve();}
}
A string with all the same character has the most palindromic substrings, so we can use many of these side by side to make a total of exactly $$$n$$$ palindromic substrings.
The idea is to use triangular numbers: the string $$$\texttt{aaa}...\texttt{aaa}$$$ with length $$$\ell$$$ has exactly $$$\binom{\ell + 1}{2}$$$ palindromic substrings. Therefore it suffices to find some triangular numbers that add up to exactly $$$n$$$.
To do this, we can greedily choose the largest triangular number less than $$$n$$$. It can be checked that the length of the string will be at most $$$300$$$ for the given constraints.
Alternatively, by Gauss's Eureka Theorem, we only need to express $$$n$$$ as the sum of three triangular numbers. We can just brute force the three triangular numbers and find the answer for each $$$n$$$.
This runs in $$$\mathcal{O}(n\sqrt{n})$$$ per test case if you lazily brute force, or $$$\mathcal{O}(n)$$$ or $$$\mathcal{O}(\sqrt{n})$$$ per test case if you use some math to find the next smallest triangular number or use precomputation.
#include <bits/stdc++.h>
using namespace std;
const int MAX = 200007;
const int MOD = 1000000007;
void solve() {
int n;
cin >> n;
char curr = 'a';
int it = 0;
while (n > 0) {
int now = 0;
while (((now + 1) * (now + 2)) / 2 <= n) {now++;}
cout << string(now, ('a' + it));
n -= (now * (now + 1)) / 2;
it++;
}
cout << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int tt; cin >> tt; for (int i = 1; i <= tt; i++) {solve();}
}
Brute force small $$$n$$$ and find a pattern.
Here is a rough idea: for large $$$n$$$, the smallest number we can make by turning on segments should have a lot of $$$8$$$s at the end (since $$$8$$$ has the most segments), and the largest number we can make should have a lot of $$$1$$$s at the end (since $$$1$$$ has the fewest segments, so we can put more of them next to each other).
Therefore, the intended solution goes as follows: write a brute force for small $$$n$$$ ($$$n \leq 30$$$, say), and find the smallest and largest numbers after turning on $$$n$$$ segments. We know that these sequences should be periodic, as per the idea above, and in fact they are. The cases are as follows:
- For the largest number you can make, the pattern is $$$1$$$, $$$7$$$, $$$11$$$, $$$71$$$, $$$111$$$, $$$711$$$, $$$1111$$$, $$$7111$$$, and so on. You can see how there are lots of ones at the end of the numbers, and the prefixes start repeating eventually.
- For the smallest number you can make, the pattern is $$$1$$$, $$$7$$$, $$$4$$$, $$$2$$$, $$$6$$$, $$$8$$$, $$$10$$$, $$$18$$$, $$$22$$$, $$$20$$$, $$$28$$$, $$$68$$$, $$$88$$$, $$$108$$$, $$$188$$$, $$$200$$$, $$$208$$$, $$$288$$$, $$$688$$$, $$$888$$$, $$$1088$$$, $$$1888$$$, $$$2008$$$, $$$2088$$$, $$$2888$$$, $$$6888$$$, $$$8888$$$, $$$10888$$$, and so on. You can see how there are lots of eights at the end of the numbers, and the prefixes start repeating eventually.
This runs in $$$\mathcal{O}(n)$$$ time per test case.
I know this problem might get some criticism for being too bashy or trivialized by brute force, but I think brute forcing is an important skill to have (especially for beginners). Knowing to brute force instead of caseworking by hand is extremely useful in contests, and can also help save you time (in addition to reducing mistakes).
#include <bits/stdc++.h>
using namespace std;
const int MAX = 200007;
const int MOD = 1000000007;
int ans[15] = {-1, -1, 1, 7, 4, 2, 6, 8, 10, 18, 22, 20, 28, 68, 88};
int pref[7] = {888, 108, 188, 200, 208, 288, 688};
void solve() {
int n;
cin >> n;
if (n < 15) {
cout << ans[n];
}
else {
cout << pref[n % 7];
for (int i = 0; i < (n - 1) / 7 - 2; i++) {
cout << 8;
}
}
cout << ' ';
cout << (n % 2 ? 7 : 1);
for (int i = 0; i < n / 2 - 1; i++) {
cout << 1;
}
cout << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int tt; cin >> tt; for (int i = 1; i <= tt; i++) {solve();}
}
Solve the problem for one stack, and then use linearity of expectation for all stacks.
First, suppose there was only one stack and that $$$a_i$$$ was small. Then the answer could be easily computed by dynamic programming: $$$a_1 = 1$$$, and $$$a_i = a_{i-1} \cdot \frac{1}{2} + 0 \cdot \frac{1}{2} + 1$$$. However, $$$a_i$$$ can be up to $$$10^9$$$, so we need a way to speed this up. In fact, we can find a closed form for $$$a_i$$$: by solving the recursion, we get that $$$a_i = 2 - \frac{1}{2^{i-1}}$$$. (We can prove this by induction.) Make sure to use binary exponentiation here, because the default exponentiation function might be too slow.
Now let's solve the problem for the whole array. Note that each stack is independent. Therefore, the condition that we shoot at the stack with the smallest expected value is useless, due to linearity of expectation. Therefore, the expected number of arrows fired in total is just the sum of the expected number of arrows fired for each element.
This runs in $$$\mathcal{O}(\sum_{i=1}^n \log{a_i})$$$ time per test case.
However, you can make this run faster by noticing that for large values of $$$a_i$$$, the answer is practically equal to $$$2$$$ (this works due to the low precision). My original solution used this idea; see below for the implementation.
#include <bits/stdc++.h>
using namespace std;
const int MAX = 200007;
const int MOD = 1000000007;
long double f(long long x) {
if (x == 0) {return 0;}
if (x <= 60) {return (long double)2 - (long double)1/(1ll << (x - 1));}
return (long double)2;
}
void solve() {
int n;
cin >> n;
long long a;
long double res = 0.0;
for (int i = 0; i < n; i++) {
cin >> a;
res += f(a);
}
cout << fixed << setprecision(17) << res << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int tt; cin >> tt; for (int i = 1; i <= tt; i++) {solve();}
}
Solve the problem for one bit, and then go bit by bit to construct $$$x$$$.
Let's figure out what $$$x$$$ should be by going bit by bit in its binary representation. In particular, let $$$a_i$$$, $$$b_i$$$, and $$$x_i$$$ denote the $$$i$$$th bit from the right in $$$a$$$, $$$b$$$, and $$$x$$$, respectively. Then for all positive integers $$$i$$$:
- If $$$a_i = 0$$$ and $$$b_i = 0$$$, $$$x_i$$$ can be $$$0$$$ or $$$1$$$. However, since $$$x \leq 10^{18}$$$, it is better to set $$$x_i=0$$$ to avoid going over that limit.
- If $$$a_i = 0$$$ and $$$b_i = 1$$$, no such $$$x_i$$$ exists, and the answer is $$$-1$$$.
- If $$$a_i = 1$$$ and $$$b_i = 0$$$, $$$x_i = 1$$$.
- If $$$a_i = 1$$$ and $$$b_i = 1$$$, $$$x_i = 0$$$.
Therefore, by going bit by bit, we can construct such an $$$x$$$ or report whether no such $$$x$$$ exists. This runs in $$$\mathcal{O}(\log{n})$$$ per test case.
There is also a simpler solution not involving going bit by bit, which uses the same proof as above: just set $$$x = a \text{ XOR } b$$$, and test whether this $$$x$$$ is valid or not.
#include <bits/stdc++.h>
using namespace std;
const int MAX = 100007;
const int MOD = 1000000007;
void solve() {
long long a, b;
cin >> a >> b;
long long x = a ^ b;
if ((x | a) == (x ^ b)) {
cout << x << endl;
}
else {
cout << -1 << endl;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int tt; cin >> tt; for (int i = 1; i <= tt; i++) {solve();}
}










flamestorm simp army assemble!
flamestorm orz
flamestorm orz
flamestorm orz
flamestorm orz
flamestorm orz
flamestorm orz. Glad to see you are purple now
I think problem B can be represented in an easier(more intuitive for me) way: we can look at >< as 10, and the problem can be represented as to sort a binary string, so we can iterate over horizontal and vertical lines and count zeros and ones on subsegments with the correct direction(>< on horizontal, v^ on diagonal)
readable solutions:
can you explain solution of problem H
From linearity of expectation, you can deal with each stack independently and then sum up each stacks' results. So for one stack.
Since there is a 50% chance of reducing the stack size by 1 and 50%, we remove the entire stack. 1 is added for the current operation that we're doing
Now since $$$\mathop{{}\mathbb{E}}[0]=0$$$
From Geometric Progression summation formula.
Now as we discussed above from linearity of expectation. The final answer would just be, $$$\displaystyle F= \sum_{i=0}^N\mathop{{}\mathbb{E}}[A_i]$$$
My solutions to all of the problems.
For H you can precompute an array of the answer to the 1-stack problem for 1-100 apples then lookup arr[min(100, ai)] and add. The figures after that are negligible. That way you don't even need to find a closed form formula.
Yeah, the problem seems like it would be better if the calculation was done modulo some prime, though I think your observation is really nice, and honestly pretty funny
Thank you.
Funnily enough, the reason why I didn't do it modulo some prime is that this was my original solution :P. However the testers showed me that you could use binary exponentiation and it would work, and I thought that would be a more "standard" solution, so that's the one I used in the editorial.
Can anyone plz. explain how to solve problem I. I don't get it from editorial . and also if possible plz. tell me the approach to solve the problem like this.
The 1-bit problem has 8 cases(a=0,1; b=0,1; x=0,1) so it can be worked out easily(replace a,b,x by 0 or 1 then check the equation x or a == x xor b). You see that if a=0 and b=1 there is no solution(neither x=0 nor x=1 work). Otherwise you can pick x=0 if a=0, b=0; x=0 if a=1, b=1 and x=1 if a=1, b=0 (notice that this is the same as the 'xor' function except when a=0 and b=1 that is when there's no solution). Because 'or' and 'xor' are bitwise operations, you can build the solution bit by bit (if ai=0 and bi=1 for some position i in the bit string you can stop and output '-1' if no bit pairs are like that you have a valid solution). Alternatively you can just realize that a xor b is a solution if any solution exists. So you check if x = a xor b satisfies x or a == x xor b. If it does you output x, otherwise -1.
Also for a general approach, the hint of testing the 1-bit case probably generalizes.
I have a doubt, I am not able to understand: in the editorial of problem E, while calculating ai why we are taking last 1. I got that ai-1 will happen with probability 1/2 and 0 with 1/2 but I have a doubt in last 1. Anyone please help! Thank you!
Let $$$E[n]$$$ be expected value for a pile of length $$$n$$$, then,
$$$E[1]=1$$$
$$$E[n]= 1+(E[n-1])/2$$$
or $$$E[n]=2.(1-(1/2)^{n})$$$
Since $$$(1/2)^n$$$<<<$$$10^{-4}$$$ for $$$n>=30$$$ so, for $$$n>=30$$$ , $$$E[n]=2$$$.
So you just need to calculate $$$E[n]$$$ for $$$n<30$$$.
120425307
I was able to solve 5 problems and got 65 rank. Is it good for a newbie or bad ?? I'm new so idk how to judge myself in unrated contest.
I think that's pretty good. If we rule-of-thumb that this contest was 3 A's 3 B's and 3 C's, that means in a regular contest you would expect to solve A and B most of the time (probably more, since instead of solving another AAB like you did here, you would be spending time solving the C). I'd estimate that would get you maybe 1500-1600ish rating.
In problem E if string t has n o's and string s has (n -1) o's then I think it won't be possible to convert s to t because in such a situation if we choose two different indices in s then we will be converting one character to 'o' and other character as non — 'o' so it doesn't matter how many operations we perform we will be left with one non — 'o' in s while t is having all o's and answer should be NO. I don't know where I am going wrong because editorial says t should have atleast on 'o' for answer to be YES. Please help
The second character you convert can also be an $$$\texttt{o}$$$, since the statement says:
I think this is a better solution for Problem A: Just sort the vector and without considering the value of k just take absolute difference of first and last term.
I think this is the same as the editorial, but is a bit slower theoretically (finding minmax in $$$\mathcal{O}(n \log{n})$$$ as opposed to $$$\mathcal{O}(n)$$$).