В субботу, 12 октября, в 12.00 пройдет очередная 5-часовая тренировка на Codeforces. Уже во второй раз мы делаем отборочный контест для СГАУ, чтобы определить команды, которые поедут в Саратов (прошлогодний аналогичный контест можно найти здесь).
Как многие из вас знают, команда Teddy Bears завершила свои выступления в ACM ICPC. Это повлекло за собой переименование и перенумерацию команд. Теперь у вас есть уникальная возможность обыграть новую первую команду СГАУ и показать им, какое место они способны занять в четвертьфинале. Не пропустите свой шанс!
Контест закончился. Теперь можно просто порешать задачи или написать его виртуально.
Xellos сделал разбор задач, за что ему большое спасибо.
Now that the contest is over, I can ask: what's the solution for G? I tried to find some conditions for the tiling to exist, but every one of them failed...
if n is sum of two squares then answer is Yes
can anybody prove it?
We found this problem in old Soviet literature. But we don't want to say where exactly, because some other problems from there will appear at some programming contests soon.
About the proof: it is not so small to publish it so easy. We thought that the picture can make you think about the orthogonal triangles and their sides' lengths, that then can easily lead to the correct solution (as it happened with me when I firstly saw this problem).
Not a rigorous proof, but some ideas I used to solve problem. (Sorry for my bad English)
Lets assume that basis vectors are p1(x, y) and p2(y, -x), where gcd(x, y) = 1. Consider point (0,0). Lets find the nearest point of the same color in the same line, which belongs to our coordinate system.
k * y + b * (-x) = 0 (equation k * p1 + b * p2 = (X, 0)) Nearest solution is k = x, b = y (because gcd(x, y) = 1).
Then we can find corresponding X = x * x + y * y. It means, that colors in that line have period X. Because of gcd(x, y) = 1 each line contains all possible colors, and it have same period X.
In case gcd(x, y) != 1 each line have period X / gcd, and each consecutive gcd lines have different sets of colors, so answer is also x * x + y * y.
Как решать Е?
Найдем для каждого листа его знак(под знаком я буду подразумевать, разрешен ли ему доступ
+или нет-). По условию задачи мы можем хранить лишь вершины, с плюсами. Поэтому для всех листьев со знаком-на пути от нее до корня, а также сам корень не должны быть включены в список, иначе она получить знак+. Для оставшихся листьев мы должны найти наименьшее количество выделенных вершин, чтобы каждый лист был потомком хотя бы одной из них. Ну тут можно действовать жадно, отсортируем листья в порядке обхода в глубину. Теперь жадно идем набирая в группу несколько листьев, если у группы листьев ихLCA"наступил" на вершину, которую выделять нельзя, то группа заканчивается, иначе берем пока такое не произойдет. Ответом будет количество групп, а вершины, которые необходимо выделить это эти самыеLCA. Но еще не все, по условию было задано, что нужно среди ответов выбрать тот, который находится как можно ближе к корню, поэтому поднимаем для группыLCAпока это возможно.Спасибо.Всё понятно.
Слушай, ну у тебя какая-то наркомания. Там на самом деле достаточно проверять, все ли потомки с плюсом. Если все потомки какой-либо вершины помечены плюсом, то всегда выгодно пометить вместо этого их предка. И все. Пускаем такой DFS и он решает задачу.
Вообще, я думаю, что эту задачу решило мало народу, потому что у нее длинное условие :) Так-то там один DFS на 2 минуты.
если честно, у меня в этом контесте во многих задачах была проблема с пониманием условия. Видимо, не у меня одного... )
Да было тяжело понять, поэтому такая наркомания :)
Вообще, да.В этой задаче, например, условие было одним из самых больших.И возможно из-за этого её мало кто решил, т.к либо читали, но не поняли условие, либо просто было лень читать.
Как решать K по-человечески? Я еле запихал на плюсах Фенвика со вложенными дерамидами…
Понятно, что нужно найти количество пар точек, в которых один из них строго больше по всем параметрам. Отсортируем по возрастанию первого параметра, теперь задача свелась к следующему, есть запросы появление точки на плоскости, нужно сначала посчитать количество точек которые строго ниже и левее, а потом добавить и ее. Она же в свою очередь сводится к тому, что на некотором префиксе(все точки лежащие левее, т.е. меньше по одному из параметров) найти количество чисел строго меньших текущего числа. Дерево отрезков. Оно будет хранить деревья фенвика. Понятно, что нужно хранить лишь те значения, которые когда то появятся в данном промежутке(т.е. добавятся). Чтобы это сделать можно изначально построить дерево, а потом его использовать. В запросах сначала находим позицию в отсортированном массиве, а потом к этой позиции делаем
++. Памяти будетO(NlogN). Запрос будет обрабатываться заO(Nlog^2N).Надо объединить подсчет инверсий фенвиком и мержсортом.
У NuM nlogn. сижу курю.
Я кстати не знаю, как это доказывать)
Авторское было за
. Представим, что у нас бесконечно много памяти. Тогда понятно, как это делать двумерным Фенвиком. А теперь давайте разобьем табличку на блоки величиной 
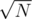, и при апдейтах для целых блоков будем использовать Фенвика (теперь уже на табличке величиной 
), а для оставшихся кусков просто запомним, где они лежат. При запросах готовые блоки опять же считаем Фенвиком, а оставшиеся куски легко подсчитать — здесь важно понять, что в каждой строке и в каждом столбце будет по одной единичке, поэтому для конкретной строки мы можем легко определить, войдет ли эта единичка в нужный нам префикс. Вот: http://pastebin.com/keQL6hQ7
Я так рассуждал: Допустим, что у нас только 2 соревнования, тогда считаем, что порядок команд в первом соревновании правильный, тогда каждое нарушение этого порядка на втором соревновании будет соответствовать требуемой паре команд. Т. е. упорядочим вторую перестановку в соответствии с первой, теперь количество инверсий в ней будет равно количеству требуемых пар команд.
Для трех соревнований заметим, что одна из команда всегда выиграла 2 раза, другая — 1 раз.
Зафиксируем какую-нибудь из таких пар команд. И пусть первая команда выигала в первых 2-х соревнованиях, а в 3-ем проиграла, тогда первое и второе соревнование не будет давать инверсию для этой команды, а соревнования 1-3 и 2-3 будут. Таким образом, просуммировав инверсии и поделив на 2, получим нужное количество.
О, понятно — вероятно, у меня то же самое) Только деление почему-то на 4)
Наверное это из-за того, что я перебираю только неупорядоченные пары. Для упорядоченных как раз получается деление на 4.
У меня за
O(N*sqrt(N). 6 sqrt-декомпозиций, по каждой паре параметров. Я понятия не имею, как оно работает и почему, если кто-то объяснит — буду благодарен. Я думал, что это какая-нибудь формула включений-исключений, но не похоже. Исходник: 4759731.Ну и если я правильно понимаю, то можно сделать все то же самое за
N*log(N)с помощью дерева отрезков — я в нем не особо разбираюсь, так что исправьте меня, если я ошибаюсь.Can someone provide a hint or algorithm for Problem I (Meteor Shower). It seems to be a DP problem but I am unable to formulate the DP, if any.
I'll write something about all problems. Just wait.
Here It's not DP, at least not as far as I can see.
in gym,when i turn the coach mode off,i find that the web page show that i have ac all the problem,what happened?
in gym,when i turn the coach mode off,i find that the web page says that i hava ac all the problem,why?
You (or your teammate?) have sent all jury solutions in the coach mode.
Как решались F? Было ощущение, что в F какие-то диофантовы уравнения
Бинпоиск по ответу)