1516A - Tit for Tat
The general approach to minimizing an array lexicographically is to try to make the first element as small as possible, then the second element, and so on. So greedily, in each operation, we'll pick the first non-zero element and subtract $$$1$$$ from it, and we'll add that $$$1$$$ to the very last element. You can make the implementation faster by doing as many operations as you can on the first non-zero element simultaneously, but it's not necessary.
Code link: https://pastebin.com/pBsychs2
1516B - AGAGA XOOORRR
So let's try to understand what the final array looks like in terms of the initial array. The best way to see this is to look at the process backwards. Basically, start with the final array, and keep replacing an element with the $$$2$$$ elements that xor-ed down to it, until you get the initial array. You'll see that the first element turns into a prefix, the second element turns into a subarray that follows this prefix, and so on. Hence, the whole process of moving from the initial to the final array is like we divide the array into pieces, and then replace each piece with its xor, and we want these xors to be equal. A nice observation is: we need at most $$$3$$$ pieces. That's because if we have $$$4$$$ or more pieces, we can take $$$3$$$ pieces and merge them into one. Its xor will be the same, but the total piece count will decrease by $$$2$$$. Now, checking if you can divide it into $$$2$$$ or $$$3$$$ pieces is a simple task that can be done by bruteforce. You can iterate over the positions you'll split the array, and then check the xors are equal using a prefix-xor array or any other method you prefer.
Additional idea: for $$$2$$$ pieces, you don't even need bruteforce. It's sufficient to check the xor of the whole array is $$$0$$$. Hint to see this: write the bruteforce.
Code link: https://pastebin.com/tnLpW23C
Bonus task: can you find an $$$O(n)$$$ solution? What if I tell you at least $$$k$$$ elements have to remain instead of $$$2$$$?
1516C - Baby Ehab Partitions Again
First of all, let's check if the array is already good. This can be done with knapsack dp. If it is, the answer is $$$0$$$. If it isn't, I claim you can always remove one element to make it good, and here's how to find it:
Since the array can be partitioned, its sum is even. So if we remove an odd element, it will be odd, and there will be no way to partition it. If there's no odd element, then all elements are even. But then, you can divide all the elements by $$$2$$$ without changing the answer. Why? Because a partitioning in the new array after dividing everything by $$$2$$$ is a partitioning in the original array and vice versa. We just re-scaled everything. So, while all the elements are even, you can keep dividing by $$$2$$$, until one of the elements becomes odd. Remove it and you're done. If you want the solution in one sentence, remove the element with the smallest possible least significant bit.
Alternatively, for a very similar reasoning, you can start by dividing the whole array by its $$$gcd$$$ and remove any odd element (which must exist because the $$$gcd$$$ is $$$1$$$,) but I think this doesn't give as much insight ;)
Code link: https://pastebin.com/aiknVwkZ
1516D - Cut
Let's understand what "product=LCM" means. Let's look at any prime $$$p$$$. Then, the product operation adds up its exponent in all the numbers, while the LCM operation takes the maximum exponent. Hence, the only way they're equal is if every prime divides at most one number in the range. Another way to think about it is that every pair of numbers is coprime. Now, we have the following greedy algorithm: suppose we start at index $$$l$$$; we'll keep extending our first subrange while the condition (every pair of numbers is coprime) is satisfied. We clearly don't gain anything by stopping when we can extend, since every new element just comes with new restrictions. Once we're unable to extend our subrange, we'll start a new subrange, until we reach index $$$r$$$. Now, for every index $$$l$$$, let's define $$$go_l$$$ to be the first index that will make the condition break when we add it to the subrange. Then, our algorithm is equivalent to starting with an index $$$cur=l$$$, then replacing $$$cur$$$ with $$$go_{cur}$$$ until we exceed index $$$r$$$. The number of steps it takes is our answer. We now have $$$2$$$ subproblems to solve:
calculating $$$go_l$$$
To calculate $$$go_l$$$, let's iterate over $$$a$$$ from the end to the beginning. While at index $$$l$$$, let's iterate over the prime divisors of $$$a_l$$$. Then, for each prime, let's get the next element this prime divides. We can store that in an array that we update as we go. If we take the minimum across these occurrences, we'll get the next number that isn't coprime to $$$l$$$. Let's set $$$go_l$$$ to that number. However, what if $$$2$$$ other elements, that don't include $$$l$$$, are the ones who aren't coprime? A clever way to get around this is to minimize $$$go_l$$$ with $$$go_{l+1}$$$, since $$$go_{l+1}$$$ covers all the elements coming after $$$l$$$.
counting the number of steps quickly
This is a pretty standard problem solvable with the binary lifting technique. The idea is to perform many jumps at a time, instead of $$$1$$$. Let's calculate $$$dp[i][l]$$$: the index we'll end up at if we keep replacing $$$l$$$ with $$$go_l$$$ $$$2^i$$$ times. Clearly, $$$dp[i][l]=dp[i-1][dp[i-1][l]]$$$ since $$$2^{i-1}+2^{i-1}=2^i$$$. Now, to calculate how many steps it takes from index $$$l$$$ to index $$$r$$$, let's iterate over the numbers from $$$log(n)$$$ to $$$0$$$. Let the current be $$$i$$$. If $$$dp[i][l]$$$ is less than or equal to $$$r$$$, we can jump $$$2^i$$$ steps at once, so we'll make $$$l$$$ equal to $$$dp[i][l]$$$ and add $$$2^i$$$ to the answer. At the end, we'll make one more jump.
Code link: https://pastebin.com/Ng314Xc8
1516E - Baby Ehab Plays with Permutations
Let's think about the problem backwards. Let's try to count the number of permutations which need exactly $$$j$$$ swaps to be sorted. To do this, I first need to refresh your mind (or maybe introduce you) to a greedy algorithm that does the minimum number of swaps to sort a permutation. Look at the last mismatch in the permutation, let it be at index $$$i$$$ and $$$p_i=v$$$. We'll look at where $$$v$$$ is at in the permutation, and swap index $$$i$$$ with that index so that $$$v$$$ is in the correct position. Basically, we look at the last mismatch and correct it immediately. We can build a slow $$$dp$$$ on this greedy algorithm: let $$$dp[n][j]$$$ denote the number of permutations of length $$$n$$$ which need $$$j$$$ swaps to be sorted. If element $$$n$$$ is in position $$$n$$$, we can just ignore it and focus on the first $$$n-1$$$ elements, so that moves us to $$$dp[n-1][j]$$$. If it isn't, then we'll swap the element at position $$$n$$$ with wherever $$$n$$$ is at so that $$$n$$$ becomes in the right position, by the greedy algorithm. There are $$$n-1$$$ positions index $$$n$$$ can be at, and after the swap, you can have an arbitrary permutation of length $$$n-1$$$ that needs to be sorted; that gives us $$$n-1$$$ ways to go to $$$dp[n-1][j-1]$$$. Combining, we get that $$$dp[n][j]=dp[n-1][j]+(n-1)*dp[n-1][j-1]$$$.
Next, notice that you don't have to do the minimum number of swaps in the original problem. You can swap $$$2$$$ indices and swap them back. Also, it's well-known that you can either get to a permutation with an even number of swaps or an odd number, but never both (see this problem.) So now, after you calculate your $$$dp$$$, the number of permutations you can get to after $$$j$$$ swaps is $$$dp[n][j]+dp[n][j-2]+dp[n][j-4]+...$$$. Now, let's solve for $$$n \le 10^9$$$.
Sane solution
Notice that after $$$k$$$ swaps, only $$$2k$$$ indices can move from their place, which is pretty small. That gives you a pretty intuitive idea: let's fix a length $$$i$$$ and then a subset of length $$$i$$$ that will move around. The number of ways to pick this subset is $$$\binom{n}{i}$$$, and the number of ways to permute it so that we need $$$j$$$ swaps is $$$dp[i][j]$$$. So we should just multiply them together and sum up, right? Wrong. The problem is that double counting will happen. For example, look at the sorted permutation. This way, you count it for every single subset when $$$j=0$$$, but you should only count it once. A really nice solution is: force every element in your subset to move from its position. How does this solve the double counting? Suppose $$$2$$$ different subsets give you the same permutation; then, there must be an index in one and not in the other. But how can they give you the same permutation if that index moves in one and doesn't move in the other?
So to mend our solution, we need to create $$$newdp[n][j]$$$ denoting the number of permutations of length $$$n$$$ which need $$$j$$$ swaps to be sorted, and every single element moves from its position (there's no $$$p_i=i$$$.) How do we calculate it? One way is to do inclusion-exclusion on the $$$dp$$$ we already have! Suppose I start with all permutations which need $$$j$$$ swaps. Then, I fix one index, and I try to subtract the number of permutations which need $$$j$$$ swaps to be sorted after that index is fixed. There are $$$n$$$ ways to choose the index, and $$$dp[n-1][j]$$$ permutations, so we subtract $$$n*dp[n-1][j]$$$. But now permutations with $$$2$$$ fixed points are excluded twice, so we'll include them, and so on and so forth. In general, we'll fix $$$f$$$ indices in the permutation. There are $$$\binom{n}{f}$$$ ways to pick them, and then there are $$$dp[n-f][j]$$$ ways to pick the rest so that we need $$$j$$$ swaps. Hence: $$$newdp[n][j]=\sum\limits_{f=0}^{n} (-1)^f*\binom{n}{f}*dp[n-f][j]$$$. Phew!
If you have no idea what the hell I was talking about in the inclusion-exclusion part, try this problem first.
Code link: https://pastebin.com/3CzuGvtw
Crazy solution
Let $$$[l;r]$$$ denote the set of the integers between $$$l$$$ and $$$r$$$ (inclusive.)
Let's try to calculate $$$dp[2n]$$$ from $$$dp[n]$$$. To do that, we need to understand our $$$dp$$$ a bit further. Recall that $$$dp[n][j]=dp[n-1][j]+(n-1)*dp[n-1][j-1]$$$. Let's think about what happens as you go down the recurrence. When you're at index $$$n$$$, either you skip it and move to $$$n-1$$$, or you multiply by $$$n-1$$$. But you do that exactly $$$j$$$ times, since $$$j$$$ decreases every time you do it. So, this $$$dp$$$ basically iterates over every subset of $$$[0;n-1]$$$ of size $$$j$$$, takes its product, and sums up!
Now, let's use this new understanding to try and calculate $$$dp[2n]$$$ from $$$dp[n]$$$. suppose I pick a subset of $$$[0;2n-1]$$$. Then, a part of it will be in $$$[0;n-1]$$$ and a part will be in $$$[n;2n-1]$$$. I'll call the first part small and the second part big. So, to account for every subset of length $$$j$$$, take every subset of length $$$j_2$$$ of the big elements, multiply it by a subset of length $$$j-j_2$$$ of the small elements, and sum up. This is just normal polynomial multiplication!
Let $$$big[n][j]$$$ denote the sum of the products of the subsets of length $$$j$$$ of the big elements. That is:
Then, the polynomial multiplication between $$$dp[n]$$$ and $$$big[n]$$$ gives $$$dp[2n]$$$! How do we calculate $$$big$$$ though?
Notice that every big element is a small element plus $$$n$$$. So we can instead pick a subset of the small elements and add $$$n$$$ to each element in it. This transforms the formula to:
Let's expand this summand. What will every term in the expansion look like? Well, it will be a subset of length $$$l$$$ from our subset of length $$$j$$$, multiplied by $$$n^{j-l}$$$. Now, let's think about this backwards. Instead of picking a subset of length $$$j$$$ and then picking a subset of length $$$l$$$ from it, let's pick the subset of length $$$l$$$ first, and then see the number of ways to expand it into a subset of length $$$j$$$. Well, there are $$$n-l$$$ elements left, and you should pick $$$j-l$$$ elements from them, so there are $$$\binom{n-l}{j-l}$$$ ways to expand. That gives use:
But the interior sum is just $$$dp[l]$$$! Hurray! So we can finally calculate $$$big[n][j]$$$ to be:
And then polynomial multiplication with $$$dp[n]$$$ itself would give $$$dp[2n]$$$. Since you can move to $$$dp[n+1]$$$ and to $$$dp[2n]$$$, you can reach any $$$n$$$ you want in $$$O(log(n))$$$ iterations using its binary representation.
Code link: https://pastebin.com/yWgs3Ji6
Bonus task-ish: the above solutions can be made to work with $$$k \le 2000$$$ with a bit of ugly implementation, but I don't know how to solve the problem with $$$k \le 10^5$$$. Can anyone do it? The sane solution seems far off, and I don't know if it's possible to do the convolution from $$$dp$$$ to $$$big$$$ quickly in the crazy one.










Such a nice round without any ad-hoc question, thank you <3
O(n) solution for B 113732376
Hint:
let,
xr = xor(a0...an)if xr is 0 then the answer is yes because its always possible to divide in 2 parts, otherwise we need to divide the array into 3 or more segments whose xor = xr.
this can be done in O(n) because we are removing adjacent elements.
"otherwise we need to divide the array into 3 or more segments whose xor = xr."
Could you elaborate how to implement that in O(n)?
See my solution buddy ( 113732376 )
Will you please explain why xor should be equal to xr?
We have to divide array into segment with equal value, let say x,
So,
x^x^x... = xr (since, xr > 0, no. of x's must be odd)
=> (0)^x = xr
So x must be xr.
what do u mean by (0) in the implication?
(0) means 0, sorry for the brackets.
Hey, i had a small doubt regarding your solution. I understand that the array needs to be divided into 3 parts x^x^x,
lets say the xor of entire array is xr and was not 0
so the array has to be of the form x^x^x where x is xor of some segment right...So we traverse from beginning and notice when does our new-xor (say nxor) become equal to xr, if that hits, that means our array is of the form
nxor^x^x = xr
I want to know why is it crucial to check any furthur, we now know that x^x will essentially be 0 because nxor^x^x = xr, and nxor became equal to xr at some point. This approach fails.
Can you point out whats wrong here or give a simple Test Case for this approach to fail. Thanks :)
Try this test case,
4
3 1 3 2
Thanks, understood... :)
Hi, Could you explain why the array must be divided into three parts? Thanks.
Dividing the array into 3 parts is the bare minimum if the xor of entire array was not 0. By dividing we are actually simulating the fact that the entire array is reduced to [x, x, x] where x is the xor of segments. The question asks us if we can reduce the array to this form. Obviously if we can reduce the array to anything greater than this it should be of the form [x, x, x, x,........ x] for this the bare minimum possibility is [x, x] but you see in this case the xor of entire array will be 0. So for cases where the entire xor is NOT 0, we need to divide the array into AT LEAST 3 segments or more. where the xor of each segment is equal.
When xor of array is zero does that imply there's a prefix xor which is equal to the xor of remaining suffix part?
Yes, infact every prefix xor will be equal to its suffix xor.
Yes I just realized this interesting property. Because if not, then prefix ^ suffix will not yield zero.
Actually 2 or more segments whose xor = xr is enough, I submitted ur exact same code with (c >= 2) and it passed ! EDIT : that's becuase if it can be divided into 2 parts then xr would be 0 and we wouldn't even have to divide it into parts.. (I just realized that)
Yes, that's true but you'll never get c = 2,4,6... Because we already considered the case when xor = 0.
can you please tell me how did you get to the approach that we need 3 or more segments whose xor = xr? I am finding it a bit difficult in getting it.
It was mentioned in the Question that the segments must be >=2 , but we already considered the case when segment = 2 (xor =0), so segments must be >=3
nice solution.
i am just a little salty about how i didnt notice the word "adjacent" in div2 b's statement until someone told me after the contest. if the problem was restated with "adjacent" is it still doable in the TL?
Could someone please elaborate on the knapsack part of the C problem?
since we need to partition the array into subsequence with equal sum . let's denote the sum of all the elements in the array as sum(array). we can reduce the problem to find whether we can find some elements of the array which add up to sum(array)/2. [ therefore , making the sum of the rest of elements = sum — sum(array)/2 = sum(array)/2 ] this is the problem that we solve with 0/1 knapsack dp ( i.e for each elements check whether it can be taken or not to make the required sum ) ;
At first,suppose S = 0 and a is given array.
for each element in a, if you put it in group1, you just add it to S. Else if you put it in group2,you substract it from S instead.
If you can separate them in two groups of the same sum — value, you can make S equal to 0 at the end.
dp[index][value] = bool(you can S = value + sum(a),when you itereate a[1]...a[idx]) note that value can be negative.
here DP works(sorry not C++ coding.)
At last, you just check whether DP[n][sum(a)] = true or not.
Thanks for the great round and fast tutorial!
Yet another Ehab voodoo :") Nice problem btw
Why wont just finding the minimum element work in C after checking the intial knapsack condition, why are we checking trailing zeros?
consider the following input
5
2 2 2 3 3
initially [2, 2, 2] == [3, 3] but after removing 2 you can do [2, 3] == [2, 3] you can multiply all of these input values by 2.... and you'll have to do it by "trailing zeroes"
after removing 2 you mean. Damn i got confused for a while
oops mea culpa. fixed now
Can you please explain the logic behind removing element with minimum tailing zeros? Thanks in advance
consider
2 2 2 2 3 3
sums to 14 (3+2+2). Remove a 2, and it sums to 12 (3+3).
In Problem E, isn't the recursion under the heading "Sane Solution", still $$$O(n)$$$, how have we optimized that?
Go back to the first paragraph where I motivate $$$newdp$$$. We only calculate $$$newdp$$$ up to $$$n=2k$$$. Sorry if reusing "$$$n$$$" confused you.
The solution is very confusing for me, but I found this during the contest and now I have an $$$O(klog(k)log(n))$$$ solution. Hope you would find it nice: Let $$$f_n = \sum\limits_{k \geq 1} T(n, k)x^k$$$, where $$$T(n, k)$$$ is defined in the link. The recursion for $$$T(n, k)$$$ is same as that of $$$dp[n][k]$$$. Now you can write recursion for $$$f_n$$$ as follows:
where $$$f_2 = \frac{x}{1-x}$$$ Define $$$g_n = 1 + f_n$$$, so $$$g_2 = \frac{1}{1-x}$$$. We then have,
Therefore, $$$g_n = \frac{(1+2x)(1+3x)..(1+(n-1)x))}{1-x}$$$ for $$$n > 2$$$. We are concerned till coefficient of $$$x^k$$$ only. So using divide and conquer and applying NTT, we can find the coefficients in $$$O(klog(k)log(n))$$$.
Hoping you liked it.
Why not define $$$\displaystyle f_n = \sum_{k \geq 0} dp[n][k] x^k$$$ ?
Which can significantly reduce the cost of reading your comment.
note that $$$f_2 = 1 + x$$$ but not $$$\frac{x}{1 - x}$$$, and
using divide and conquer and applying NTT with $$$O(k \log k \log n)$$$ also two slow. Even can't pass the original problem(maybe my implement $$$O(k^2 \log n)$$$ is two slow? but $$$k^2$$$ and $$$k\log k$$$ has no much difference).
UDP: Sorry, Hugin's 113874644 is the correct implement.
Considering mohammedehab2002 is the setter.
O(sum*n*log(2048)) Solution for Div2C : 113753603
The answer to problem E is actually $$$ F(n,m) = \sum_{i \leq m, i \equiv m \bmod 2} S_1(n,n - i)$$$ where $$$S_1$$$ denotes to the first kind of Stirling number.
So the task is basically to calculate the last $$$k$$$ terms of $$$S_1(n)$$$. With Lagrange interpolation, you can easily get a $$$O(k^2)$$$ solution (or $$$O(k^3)$$$, if not well implemented). Not sure if you can solve $$$k \leq 10^5$$$.
For bonus on B:
For $$$O(n)$$$ solution, it is enough to check if the whole array xor appeared as a prefix xor, and between them, there is a $$$0$$$.
For $$$k$$$, if we generalize the previous solution, there is an answer when there is a prefix xor subsequence like $$$P 0 P 0 P ...$$$, atleast $$$k$$$ times, where $$$P$$$ is the xor of the whole array.
But, if $$$P = 0$$$, then we should check for that subsequence for each prefix xor.
Hey, I didn't get the solution for k. Could you explain it in detail, please?
Please share your code for at least k elements with equal xor
In the first problem it says choose 2 different elements doesn't that mean it has to be 2 distinct elements(both of them are not equal) (I considered that only and solved it :/) PROBLEM WAS UNCLEAR WHICH IS QUITE UNFAIR
I understood it in a same way, so I checked it by "asking the question" to the authors. So on one hand I agree with you, that it could (should) have been stated better, on other hand you can always verify it with the authors during the contest
For each i(1,n-2): (0 indexed) If left_xor(i-1) == right_xor(i): Cout... Yes Return
Cout...No
My thought process is that the two element in the end will be formed by leftmost subarray and the rightmost subarray. (Since we can merge only adjacent numbers)
Why this will not work can someone please explain??
try this :
Tag $$$B$$$ as a DP problem. I solved it with DP lol
Here
Could you explain your how your solution works?
Nasty test-case 16.
could anyone who solved problem D using segment tree tell their solution ?
WA16Forces
In C, after checking for odd elements, why will just removing the smallest number not work?
check here
Thanks, got it!
Consider this,
Check this for an intuitive approach to this problem
Some people passed C with
(sum*n)*n = 2e9by bruteforcing and checking after removal of every element. Was that intended?It is so not obvious that it can always be solved by removing no more than one element that I think it is fine
Hi everyone! I was the first person to pass the pretest for problem C (prior to it failing on the added pretests), and was probably the reason why authors had to add the tests. I want to give my perspective on the incident.
I started the contest trying to solve C first, hoping to get the first AC. It took a bit of thinking, but I quickly figured out how to remove at most one element and get a good array. I went on to implement the solution, but in the haste I forgot to check if the array was already good! I submitted the solution, it (somehow) passed pretests and I went on to solve the other problems without giving it much thought, other than wondering why the constraints were so low.
Then there was an announcement saying that more tests have been added, but I brushed it off thinking it was no big deal. Only after solving the first 4 problems and taking a quick look at the standings did I realize my solution on C had now failed pretests! Upon checking the solution again, I noticed what the low constraints was for, and knew where my solution was wrong. I sighed, fixed the solution, and now it passed pretests for sure.
In the end though, I found the whole thing pretty funny, albeit a bit annoying since I couldn't get the first AC. While I know the situation can be frustrating for many participants and I think these types of errors should have been included in pretests in the first place (or not entirely), I'm not putting the blame on authors. It is only a small part in the whole contest-writing process and I understand that mistakes like this can sometimes happen. In fact, I should probably thank them for adding the tests since if not, I wouldn't have noticed that my solution was wrong and it probably would have FST'd!
mohammedehab2002 anything you want to add?
Edit: It's worth mentioning that my first solution had some failsafes that would return 0 if the sum of the array was odd after repeatedly dividing all elements by 2, which makes it a bit harder to generate counter-tests, as written in the reply below.
Hi!
Yes, that's what happened. The whole story is: problem C originally had $$$n \le 24$$$ and $$$a_i \le 10^9$$$. That didn't work out very well in the official contest, because of some hacky ideas. However, it was better for test data generation, because if you want to generate a case where the answer is $$$0$$$, any random case would do, since $$$n \ll a_i$$$. I focused so much on generating cases where you need to remove an element (e.g. fail solutions which remove the minimum or a random element until it works etc.) When I migrated to $$$n$$$ close to $$$a_i$$$, I should've shifted the focus to cases where you don't remove anything. It's actually really hard to make a big case where no partitioning exists, and my weak-ass generators could only do it by adding a case where the sum is odd. I found cases where the answer is $$$0$$$, but I didn't realize it was because the sum is odd.
After I saw your solution, I thought it was best to add pretests, because it would be much more chaotic not to. I think very few div.2 participants got affected, since the whole thing was 20 mins after the beginning or so.
Thanks for saving us ;)
I tried to solve D with Mo algorythm. Since we basically search for the frequency of the max freq primefactor in range l,r, that should work.
But it still gives WA, and I cannot find a counterexample for my code. Somebody explain why Mo does not work at all, or where my implementation is wrong? 113791577
incorrect approach
see this tc-
6 1
5 2 2 2 5 5
1 6
correct=4
your op=3
Ah, I see. Thanks a lot!
Problem E is googleable. Notice that the number permutations of size $$$n$$$ having $$$k$$$ cycles are exactly Stirling numbers of the first kind. So for each $$$i$$$ from $$$1$$$ to $$$k$$$ we have to find $$$[n, n - i]$$$. And according to this,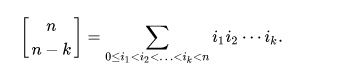
And, a faster algorithm to solve the exact same equation has been discussed here by zscoder (check the last trick). I think using the idea from here problem E can be solved in $$$O(k \, log(k) \, log(n))$$$ using NTT.
Another thing to note here is that the problem can also be solved using Interpolation. Solve for smaller $$$n$$$, construct the polynomial and get the answer for larger $$$n$$$.
please mohamed ehab try to but the base case in pretest it is not funny every contest to put base case in main test pretest is for making codeforces faster during the contest not to make people wrong in main test
Hey could anyone explain why im not getting tle in problem C? https://codeforces.me/contest/1516/submission/113792684 In my solution im not dividing by 2(for all even array) as in the editorial. I'm simply looping for all possible elements and checking if by removing that element (making it 0) we can make the sum(either odd) or if there is no such partition so that array can be divided in two subsequences with equal sum by DP in o(n*sum). Shouldnt the complexity be O(n^2*sum) in the worst case? I did not try this solution in the contest because i was convinced that it wouldnt pass but after looking at codes of other people i submitted my brute force soln which passed to my horror!
if in d, instead of subrange, it was subsequence is there better order than N * sqrt(n) * log(n) ?
I am having trouble understanding the 3 pieces logic in B problem. Can someone just give an example on how the algorithm is working.
thanks!
think if it this way you have an array A of size N which can be split into say x pieces where each of them produce equal xors , I am taking a case where x is odd for now.
A-> [a,a,a,a,.. x pieces] So as we are allowed to xor adjacently.. maybe I take the first two a's and xor them
A-> [a^a,a,a,a,.. x-1 pieces]
A-> [0,a,a,a,a,.. x-1 pieces]
xoring first two elements again
A-> [0^a,a,a,a,... x-2 pieces]
A-> [a,a,a,a,.. x-2 pieces]
and hence with this continued you can reach any odd pieces you wish ...
x=3 is desired ...
I solved B in O(n): https://codeforces.me/contest/1516/submission/113728841
For problem B, i think if we do xor of full array and if it is 0, then YES else NO
[4, 7, 7, 4, 1, 4, 6] — Here if we xor all the items, it is 0 hence YES [2 3 1 10] — Here if we xor all the items, it is not 0, hence NO
I dont understand why I get wrong answer for this.
Can someone please suggest a case where xor of all items is 0, but still answer is YES. I tried going through the editorial, but I dont understand the 3 partition. Any help is appreciated.
Sorry for typo in my previous comment. I am looking for a case where xor of all items is not 0, but still answer is "YES" (except single element)
In above case, xor of all elements is not 0, but still answer is "YES".
UP: 3 is the number of element. Elements are [5,5,5]
Sorry I dont understand. [3, 5, 5, 5]
if we do xor of 0th and 1st we get [6, 5, 5] do it again we get [3, 5] hence NO
if we do xor of 1st and 2nd we get [3, 5, 5], do it again we get [3, 5], hence NO
am I missing something?
You don't have to reduce it to exactly 2 groups, read the question once again.
I did knapsack dp for problem C.
Then if sum / 2 is achievable by a subsequence,
I take the minimum element of the array as the element to be removed.
This gives WA on pretest 6.
Any counter case on why this fails ?
This was so intuitive for me and couldn't get where this fails.
https://codeforces.me/blog/entry/89846?#comment-782759
think of the case {8,8,6,6,4,4,4,4}
In Problem C , is someone having a better proof of the claim that with removing at most one element we can make it a good array, It is not mathematically satisfying that if we have some property for numbers a,b,c it will work for 2*a,2*b,2*c as well , Re scaling cannot be a thorough argument....
Most of the people here are asking why didn't removing smallest element work (given partitioning is possible and all elements are even).. Think it this way .. You have this array -> 8,8,4,4,4,4,6,6
A Possible Partitions is {8,6,4,4} , {8,6,4,4} ,
so If you remove 4 which is the smallest element, The difference in the subset Sum you have now made is 4, so you need to compensate with this difference so you can simply swap 8 and 6 between two subsets to compensate this difference created, So Subsets Left Now will be {8,4,4,4} and {8,6,6}, more mathematically if S is the total sum so your Subsets have sum S/2 each let Min be the element you want to remove so now subsets will be come S/2- Min and S/2 and now to equalise subsets look for swapping two elements between arrays -> x,y such that x > y && S/2 — Min — y + x = S/2 — x + y
Re-scaling can’t always be a good argument, but in this case it’s completely correct. As mentioned in the editorial, if there is a good partition of an array, that partition will also be good if we multiply all numbers by 2 (let the sums be s1 and s2, if s1 = s2, then 2*s1 = 2*s2). I don’t see a problem with that proof.
Thanks for replying actinium16 , Maybe I am expecting something more convincing .. Not able to prove it in my head that why always removing one is enough maybe you can help me with that by little elaboration.
Well, if you accept the mentioned proof as correct, you see you can just divide all the numbers by 2 until some of them become odd. Now, if the sum is odd, there is already no good partition, so the answer is 0. If it's even and there is a good partition, you can remove an odd number and the sum will become odd, which means there will again be no good partition. As for the proof, I'm not really sure how to explain it better, but try thinking of it this way: if there is a good partition, then we can divide the array into 2 arrays (let's call them A and B) such that A1 + A2 + ... + Ax = B1 + B2 + ... + By. Now, suppose we multiply all the elements by 2. The sums of numbers in arrays A and B will be 2*(A1 + A2 + ... + Ax) and 2*(B1 + B2 + ... + By), and we can see that they are equal again.
Cool..It was hard to digest the other way round when you had the array and you were dividing stuff to get to an odd element .. and then choose it to be removed..
But thinking the other way with starting from the array with an odd element and then multiplying by 2 seems more convincing idea..
Thanks actinium16
No problem
What happens if all numbers were even ?
You divide all of them by 2 until some of them become odd
I don't get the logic behind it, since the operation allowed is only deleting elements
Another question is the knapsack part I couldn't figure it out if u can help it'd be great
For the first part, take a look at my comment above.
For the knapsack part, you can have dp[ind][sum], where ind denotes the current index in the array and sum denotes the sum of numbers you need. Now, we can do 2 different things: we can skip the element at the current index (just go on to dp[ind+1][sum]), or we can take that element and go to dp[ind+1][sum-a[ind]].
I'm thinking of it like this: it's simple to prove that if all numbers are integers and you can just remove an odd number it will work.
However there isnt anything particular about the individual numbers as the partitions will be exactly the same for {a,b,c,d,e,f} and {a/x, b/x, c/x, d/x, e/x, f/x}, the only difference is that the sum of the first one will be s1/x and the second s2/x.
Then, i'm just going to pick x so that the sequence will remain with integers and at least one of the elements will be odd, since by the previous argument it will obey the same properties and solve it from there
Thank you for elaborate idea defnotmee
I've explained a proof with details. You might want to check my comment.
Me who understood how to solve 2nd problem when 4 mins were left and i didnt have enough time to write the solution :)
Amazing problems in this one. Thanks mohammedehab2002
For problem B, how can we partition this array?
PS: This is TC 16!
[3][3][3 0]
i feel really dumb now -_-
"keep dividing by 2. If I get any odd number remove it"
Please explain why it works?
https://codeforces.me/blog/entry/89846?#comment-782951 check this out.
Thanks a lot. I was looking for it.
You can always do at most 1 operation and solve the problem. If $$$sum$$$ of array is odd,then answer is obviously 0, if $$$sum$$$ is even and $$$sum/2$$$ is odd, then you can remove any odd element which will always exist since you can divide array into two parts with odd sum in each part, if $$$sum/2$$$ is even then youu need to check whether it is possible to make { $$$\ newsum=sum-a_i\ $$$ } newsum/2 from the given array and print the desired $$$a_i$$$.
Solution
Really Cool approach! Thanks
in problem B someone please explain this
A nice observation is: we need at most 3 pieces. That's because if we have 4 or more pieces, we can take 3 pieces and merge them into one. Its xor will be the same, but the total piece count will decrease by 2.
"Merging 3 pieces into one" means, that if you got three equal elements, you can once merge two of them to get 0, then merge that 0 with the last one to be left with only one elment instead of 3.
So there is no need to consider cases where we have more than 3 partitions, because they behave like we would have 2 or 3.
Can you explain with an example ?
x^x^x = x^(x^x) = x^0 = x
We can substitute each triple by one occurence.
Your final answer should have all the elements equal, and should have atleast two elements.
Let's say your final answer looks like:
Case: [a a a a]
Now here you should notice that as
a^a^a = ayou can xor the first 3 elements and get [a, a]Case: [a a a a a]
You can xor first 3 elements, so final array would become [a, a, a].
You can always transform an even length array of equal elements to size 2 and odd length array to size 3.
Can someone please explain this part in C's editorial
** But then, you can divide all the elements by 2 without changing the answer. Why? Because a partitioning in the new array after dividing everything by 2 is a partitioning in the original array and vice versa.**
Though the partitioning will remain same but sum eventually gets altered and also since we were supposed to remove some element from the array so why are we checking it by dividing every element by 2.. I'm not getting the intuition.. someone please explain it will be a great help
im copypasting a comment i did up there:
it's simple to prove that if all numbers are integers and you can just remove an odd number it will work.``However there isnt anything particular about the individual numbers as the partitions will be exactly the same for {a,b,c,d,e,f} and {a/x, b/x, c/x, d/x, e/x, f/x}, the only difference is that the sum of the first one will be s1/x and the second s2/x.Then, i'm just going to pick x so that the sequence will remain with integers and at least one of the elements will be odd, since by the previous argument it will obey the same properties and solve it from thereIn that case, X is a potency of two and that's why the editorial talks about dividing by two over and over
Thanks!
So the basically to approach this problem during the contest one should had a believe that re-scaling wont affect the partitioning properties or was there something else you thought during the contest to come up with its solution ?
Check this for an intuitive approach
Is problem D solvable using segment tree or sparse table?
Editorial uses sparse table only just in a different way.
It feels so bad when your solution fails in the system testing. Every time i close my eyes and try to sleep, i see wa.
Why does trying to remove each element from the array (n^2 * sum) not tle on C. Is it weak test data or can you prove that it doesn't tle. https://codeforces.me/contest/1516/submission/113809490 <- submission
edit: I got hacked lol edit edit: I got unhacked by sorting the array
People have explained the math approach to solving problem C but the intuition behind the solution was not clear. Specifically, when all numbers are even, keep dividing them until you get an odd — and that's the one to remove.
I finally get the intuition behind this. We need to look at it not from a numeric standpoint, but from a bit standpoint. If a given array is balanced (i.e. it can be partitioned into 2 subsets), then rather than look at the smallest number, we need to look at the number with the smallest bit set. This is because, in a balanced array, this bit (i.e. the least significant) is set an even number of times. Removing any number with this bit breaks the balance (making the number of available bits odd) such that you can't evenly split it between two groups.
Consider two examples:
1)
[1 2 3 6]This is currently balanced as you can can split it into
[1 2 3]and[6]The lowest bit is 1 and it's set in two numbers 1 and 3. Removing any one makes the array unbalanced
2)
[6 6 4 4 4]This is currently balanced as you can can split it into
[6 6]and[4 4 4]In binary notation, 6 = 110 (== 4 + 2), and 4 = 100
Note that if you removed 4 (the smallest number), it would still be balanced as you could split it into
[6 4]and[6 4]However, if you remove a 6, there's no way to partition it in a balanced manner. This is because getting rid of the 6 gets rid of the least significant bit (i.e. the second bit which has a value of 2) and there's an odd number of those bits remaining -- and no smaller bits can add up to replace it.
sh_maestro, How did you conclude that in a balanced array, the total numbers where the least significant bit is set is even ? and why is this necessary for a balanced array
Consider 5 numbers and their binary representation
[3,4,5,6,8]:Each bit that's set is a power of two that the number contributes. The lowest bit in this example is 0 (so the power of two that it contributes is (1 << 0) == 1), which is set in the two odd numbers 3 and 5. Now if you take either one away, there's no other way to make up this bit (i.e. there's no 2 bits at a lower position that can add up to this bit, since by definition, these were the least significant bits set to 1).
So either the lowest set bits need to cancel each other out (i.e. the first one goes into subset 1 and the other into subset 2 to balance them out), or they need to be put together to add up to give a higher bit (i.e two 0 bits add up to create a 1 bit — and the process repeats). There's no other way to generate this lowest bit.
ok got it
Your solution is awesome but how is it intuitive to think of lowest significant bit in the array. It only clicks if we think of lowest significant bit right..
Rather than think of significant bit, you could think of each number as contributing to multiple powers of two (for eg. 5 = 4 + 1 = 2^2 + 2^0 — i.e., 5 contributes to two powers of 2: 0 and 2), and you need to remove a number that contributes to the lowest power of two (to unbalance a balanced array). I understand it's not how we think of numbers typically but this is an alternate approach that solves the specific problem at hand.
amazing!!
mohammedehab2002 PR_0202 For div2 B, i checked for array xor 0 and equal conditions. after that if xor!=0, i traversed array and checked if every segment had value as this xor. I dont know if the logic is wrong or the implementation is wrong. my sol for ref. 113775608
I think your logic is in the wrong direction.
My approach is similar to ur approach
here is my implementation.
https://codeforces.me/contest/1516/submission/113775608
In A question, it is stated that we have to choose 2 different elements , when i saw the others code most of them applied a while loop if(arr[i] > 0 && k > 0) arr[i]-- ; arr[n-1]++ ; with outer for loop iterating from 0 to n-1.
What if arr[i] == arr[n-1] ?? It contradicts the given statement that we have to choose 2 different element .
the statement is unclear but by two different elements they didn't mean two elements with different values but two elements with different indices
Bonus of B: Let $$$X$$$ = $$$a_1$$$ ^ $$$a_2$$$ ^ ... ^ $$$a_n$$$
Let the final array be $$$b$$$ : $$$b_1$$$, ..., $$$b_m$$$, s.t. $$$b_1$$$ = $$$b_2$$$ = .. = $$$b_m$$$ = $$$k$$$
Since each $$$b_i$$$ is the xor of some subarray of $$$a$$$, it means that the xor of all elements of array $$$b$$$ = $$$X$$$
Case 1 : $$$X$$$ $$$\neq$$$ $$$0$$$
Then $$$k$$$ must be equal to $$$X$$$. Therefore we can greedily construct subarrays s.t. the xor of all elements in the subarray = $$$k$$$. Let's say that we were able to create $$$cnt$$$ such subarrays. If we were able to partition the entire array then we say the ans is $$$YES$$$ if $$$cnt$$$ is odd and $$$cnt > 1$$$, else the ans is $$$NO$$$. If it happens that some suffix of the array has xor != $$$k$$$, then we check if the xor if this suffix is = $$$0$$$. If it is $$$0$$$ then we can append it with the last subarray that had xor = $$$k$$$. Again, if the $$$cnt$$$ is odd and $$$cnt > 1$$$, then the ans is $$$YES$$$, else the ans is $$$NO$$$.
Case 2 : $$$X == 0$$$
Case 2.a : $$$k == 0$$$
Similar to above approach we try to greedily construct the solution. Here however, since $$$k == 0$$$, we do not care about the parity of $$$cnt$$$. Also, note that here, it cannot happen that some suffix of array is left, the xor of which $$$\neq 0$$$. If $$$cnt > 1$$$ the ans is $$$YES$$$, else we check case 2.b
Case 2.b : $$$k \neq 0$$$
To get $$$X == 0$$$, we want $$$cnt$$$ to be even. If this is possible, then it is also possible that $$$cnt == 2$$$ since we can merge all subarrays, maintaining parity. In the end, we would be left with 2 subarrays (a prefix and a suffix). Now, we have to a check if a prefix of the array exists s.t. xor of the prefix is equal to the xor of the corresponding suffix. This can be easily done in $$$O(N)$$$ by calculating the array $$$pref_i$$$ $$$==$$$ $$$a_1$$$ ^ ... ^ $$$a_i$$$ and then checking for each suffix xor backwards.
PS: Case 2.a is actually covered in 2.b. However, when I first attempted the problem, I did not realise it. Link to reference submission
Upd(edit): In case 2 the answer is always possible. Since $$$X == 0$$$, some prefix of the array must be equal to the suffix.
I don't fully understand. If you have X=0, you are done as you have at least 2 elements with the same value.
If you have X=k != 0, isn't it enough to check if there is some disjoint prefix and suffix with xor == k?
Yes. That works as well. It's actually a lot cleaner, but I stuck with what struck me at first glance.
Video Editorial for problem B: https://www.youtube.com/watch?v=DgY6XKYkX7c&t=1s
Thank you for such a nice explanation. What is the time complexity of this code? I am assuming O(n^2), is it right?
yes correct it is O(n^2)! Thanks for the appreciation.
A more formal formulation for the statement in the editorial of Problem $$$C$$$:
For any group of integers $$$v_1$$$, $$$v_2$$$, ..., $$$v_n$$$ that can be partitioned to $$$2$$$ subsequences with equal sums $$$v_{i_1}$$$ + $$$v_{i_2}$$$ + ... + $$$v_{i_m}$$$ $$$=$$$ $$$v_{i_m+1}$$$ + $$$v_{i_m+2}$$$ + ... + $$$v_{i_n}$$$, if we divided both sides by any common factor $$$k$$$, the equality should not be affected. This means that $$$\sum_{i=1}^{n} \dfrac{v_i}{k}$$$ is even for any common factor $$$k$$$. Hence, if we removed the element with the least $$$2^p$$$ in its factorization, we will end up with $$$\sum_{i=1}^{n} \dfrac{v_i}{2^p}$$$ being odd, which means we can not partition the array to $$$2$$$ subsequences with equal sums.
In problem C I was thinking that the number I have to remove would either be too small or too big so I tried to remove the 20 smallest numbers and 20 largest numbers and checked if there is a solution or not and got accepted. Is this just weak test cases or there is proof for this?
submission
I have provided a hack to your solution. The data generator is below:
I hope it can help you.
that helps, thanks.
Hi for question B, may I know if this is the correct idea for "at least k elements have to remain"?
I did badly for this contest, all help is greatly appreciated! :(
I think the first step is incorrect.
Consider the array $$$A = [1, 2, 4, 8, 16, 31]$$$.
The bitwise XOR of all elements is $$$0$$$, but for $$$k = 3, 4, 5, 6$$$ the answer is no.
Ahh yes you are correct. I will think over it again hmm...
Very good Round! No Weird or boring problems ! Great work Codeforces and @mohammedehab2002 ! Thanks for the Contest. We need more of these !
If k in question E is 2000,we can also use any modulus NTT to solve this problem.
Is the complexity of this algorithm $$$O(k\log k\log n)$$$ with NTT ?
nice contest without any pattern finding and ad-hoc questions
Why do we need
bitset<200005> b; b[0]=1; for (int i:v) b|=(b<<i); return b[s/2];
this piece of code (from line 11) in problem C's "bad" function?
I have the same problem, too.
I'm not able to understand solution of problem D from editorial. Can someone explain it in simple words.>_< Thanks.
I analysed and commented the code here https://pastebin.com/zbb36qBh
Hope this helps. The broad steps are:
Which of thoses steps is troublesome for you?
Thank you! I understood it now. I higly appriciate it!
Can you help me explain your code on problem C?
I am a newbie in this Knapsack. Thank you very much.
Its a faster and more advanced way for writing Knapsack using bitsets. We basically check if there is a subset with sum = s/2 where s is the sum of all elements. b[k] indicates if we have a subset with sum k possible. We iterate over all elements. The operation (b<<i) shifts the bits in b by i. Why? Because if lets say b[j]=1 (that is , sum j is possible) , then sum i+j is also possible. Then we just do b|=(b<<i) to include the effect of element i. Say if b[k] =0 initially, now we will have b[k] = 1. You can use more conventional style of writing knapsack DP as well, it works just fine.
Since s/2 is max 1e5 a bitset of half the size should also do the job.
That's amazing. Who can invent this way?
Thank you very much indeed bro, you save my day.
Problem D
"However, what if 2 other elements, that don't include l, are the ones who aren't coprime?" [3rd line of Calculating go[l] paragraph]
What does the author mohammedehab2002 mean by this. It is becoming really difficult for me to understand.
Let say we ignore that and calculate the value of go[i]. Then we will have a range i, i+1 ,i+2.................go[i] . Now lets say 2 of the elements from i+1, i+2.......go[i]-1 aren't co-prime, then we can't say that LCM = product for the range i....go[i]. Instead, we need do go[i]=min(go[i+1],go[i]). Why that works? Because go[i+1] already takes into account all elements at indices i+1,i+2,.....
Thanks a lot. I got your point.
And thank you so much for your reply.
Problem C passes O(n*n*sum(arr)).
If any element needs to be removed, I brute-forced them all which should have been TLE. Submission
In D, can anybody explain me the calculating gol part? The editorial isn't very clear to me. How are the constructing the array actually?
I analysed and commented the code. See here https://pastebin.com/zbb36qBh
I hope this helps. If something is still unclear, ask and I try to answer :)
Great job. Thank you so much. I wish I could give you two up-votes. The solution is quite complex indeed.
https://codeforces.me/contest/1516/submission/113875265 Can someone explain why this code gets Accepted for problem C instead of giving TLE ?. The approach is same as in the editorial but for the case when the array has all even elements,I am just removing one element from the array every time and calling the subset sum DP to check if it is a good array. This should take (100)*(100)*(100000)[1e9] operations to do but it still passes the test cases....
I want to give a detailed way to solve problem E in $$$O(k log(k)log(n) )$$$, we need to calculate the first k+1 term of polynomial $$$\prod_{i=1}^{n-1}(ix+1)$$$.The only tricky thing is how to calculate $$$R(x)=\prod_{i=l+m}^{len}(ix+1)$$$by the coefficient of $$$L(x)=\prod_{i=l}^{len}(ix+1)$$$. $$$R(x)=\prod_{i=l}^{len}(ix+1+mx)=\sum(mx)^i \sum \tbinom{len-i-j}{len-j}L(x)[x^j]$$$ and this can calculate by FFT easily. This is my implementation without use FFT 113874644.
Can you explain how did you expand $$$R(x)=\prod_{i=l}^{len}(ix+1+mx)=\sum(mx)^i \sum \tbinom{len-i-j}{len-i}L(x)[x^j]$$$ ? I unable to derive it.
$$$O(k \log k)$$$ approach for problem E if mod is NFT-friendly such as 998244353.
Let define $$$\displaystyle f_n = \sum_{k \geq 0} dp[n][k] x^k$$$, note that $$$f_0 = 1, f_1 = 1 + x$$$
so,
and
Note that we can compute $$$f(i) = \sum_{k = 1}^{n - 1} k^i$$$ for all $$$i < N$$$ in $$$O(N \log N)$$$ since $$$\frac{f(i)}{i!}$$$ is $$$i$$$-th coefficient of
Thus we can get $$$dp[n][j], j \leq k$$$ in $$$O(k \log k)$$$.
UDP1: Need your check: Lusterdawn mohammedehab2002
UDP2: 113886543 without NFT since mod $$$= 10^9 + 7$$$
Problem B ~~~~~ A nice observation is: we need at most 3 pieces. That's because if we have 4 or more pieces, we can take 3 pieces and merge them into one. ~~~~~
Can anyone please explain this, I couldn't understand the observation that at most 3 pieces is needed...
Let's say you have four equal elements. Your array initially looks like this : $$$a\;a\; a\;a$$$.
You can xor the first element with the second. Your array is now : $$$0\;a\;a$$$.
You can xor the first element with the second. Your array is now : $$$a\;a$$$. You have only 2 elements left.
Let's say you have five equal elements. Your array initially looks like this : $$$a\;a\; a\;a\;a$$$.
You can xor the first element with the second. Your array is now : $$$0\;a\;a\;a$$$.
You can xor the first element with the second. Your array is now : $$$a\;a\;a$$$. You have only 3 elements left.
For bigger number of pieces you can apply the same thing.
I did try to understand the program in the editorial to Problem D ( https://pastebin.com/Ng314Xc8 ). It was pretty difficult for me, so I tried annotating comments to the code. Now I understood the solution. :)
If someone is interested in those, here they are: https://pastebin.com/zbb36qBh
Hope they can help in understanding Problem D.
For problem C, the idea of continously dividing all elements by two until an odd element seems intuitive, however, I needed a proof. After some thinking, I came up with one and guess it would be helpful to those asking. We have three cases to consider :
Case 1 : We already cannot split the array into two.
This happens when either sum of all elements is odd or the sum is even but we just really can't divide them to two. (Latter can be checked with DP.) Answer is 0.
Case 2 : It can be split into two but there is at least one odd element in the array.
If we remove one of the odd numbers in the array, sum becomes odd. Since we know that the lower bound for the answer is 1, we've handled this case optimally.
Case 3 : It can be split into two and there is no odd element in the array.
If we can show that this can be handled by only removing one element (and since the answer is at least 1) , we'll be handling this case optimally too. Now consider two arrays $$$A$$$ and $$$B$$$ s.t. $$$A$$$ $$$B_i = 2*A_i$$$ for $$$i = 1 $$$ to $$$n$$$.
What we want to prove is :
If we can "break" (i.e. turning a good array into a bad one) $$$A$$$ by removing only one particular element, say, $$$A_i$$$ ;
We can remove the corresponding element $$$B_i$$$ to break $$$B$$$.
If we are able to prove this we can just continuously divide every element in our array by two until we get an array that can be handled in case 2, mark an odd element (to be removed) in our latest array, and backtrack the steps by multiplying by two, and get the element that is going to be removed. At the end, we'll be removing only one element (which is optimal).
Let's prove it with contradiction. We assume that there is such an array $$$A$$$ that we can break by removing $$$A_i$$$ but we are still able to partition $$$B$$$ even after removing $$$B_i$$$. This means there is some partition $$$[{S_1 , S_2}]$$$ of $$$B$$$ after $$$B_i$$$ is removed. We can divide all of the elements in $$$S_1$$$ and $$$S_2$$$ by two, turn any element $$$B_k$$$ in the sets $$$S_1$$$,$$$S_2$$$ into $$$A_k$$$ and name the sets into $$$S_1'$$$ , $$$S_2'$$$ . This means we can partition $$$A$$$ as $$$[S_1',S_2']$$$ and this partition doesn't contain $$$A_i$$$. But $$$A$$$ had to be broken after $$$A_i$$$ was removed. Contradiction!
UPD : If we have an array that needs to be handled at case 3 and when we continuously divide all of its elements by two, there is no way of encountering a case 1-array. Because, in a very similar matter of thinking with the above statement (which we proved), we can claim that if an array already cannot be split into two, "multiples" of this array can't be split into two either. Proof is again very similar to the above statement's.
it was a great round ty but in problem C can you explain the function bad I solve it with dp but I love to know how this function work it seems faster
You might want to check out my comment. I've explained the solution with proof and details.
Hey there, I am a new Coder trying to understand the applications of various algorithms to the questions of competitive coding. I wanted to ask whether or not we could solve problem D here with the help of range gcd query and look for coprime numbers and then increase the partitions (*2) each time until we get all partitions inside the query range with gcd=1 then the numbers will be coprime and LCM = the product. Please correct me if I am wrong somewhere. I appreciate any help.
How exactly you try to apply range-gcd queries?
Note for example the sequence "2,3,2". If you query the gcd of all 3 numbers you will get $$$gcd(2,3,2)=1$$$ but $$$lcm(2,3,2)=6 \neq 12 = 2 \cdot 3 \cdot 2$$$
I somehow doubt you can use gcd of ranges to solve this task. But maybe I just misunderstand your idea, you care to eleborate? (at least for me while solving the task I remembered $$$gcd(a,b) \cdot lcm(a,b) = a \cdot b$$$ and tried to use this for multiple inputs. But beware $$$lcm(a_i) \cdot gcd(a_i) \neq \prod a_i$$$)
what if we check for unique elements then?
Could you elaborate? Which elements do you mean? Factors? Input numbers? And how to check on them?
I somehow doubt that a pure "segment-tree" approach would work, else somebody wouldve already commented it i guess :D
and yes I know that the product of numbers= GCD*LCM holds only for 2 numbers Maybe my approach is wrong. I am not quite adept to all these mathematical thinking. Another thing, could you guide me to properly hone my skills in algo and ds...like learning resources and effective way to learn?
This is easily googleable :)
You could start e.g. here: https://codeforces.me/blog/entry/23054
Pick something from this site what you want to learn and get to it :D
I think finding the right element in the case of 1516C - Ехаб снова делит массив when the original array can be partitioned into 2 equal subsequences can be done in the following way:
Find the gcd of the elements and find the largest 2 power(2p) that divides it. There must be a number which dividided by 2p is odd since otherwise it wouldn't be maximal. If we divide the numbers by 2p we will have an even number of odd elements and we can drop any of them.
113938720 this is my solution for problem C and it got accepted but when i tried with 4 1024 1024 1024 1024 test case it still giving AC in codeforces compiler but in my compiler it does not giving any output I think 1 pretest is weak if I am wrong you are welcomed to correct me Thank you
At the end, we'll make one more jump.I'm not sure if I understood the final jump part completely in problem D. From what I understand:
During the process of binary lifting, when we make jumps to bring L closer to R, the final value of L say,
lastLwould be<= R. So we add 1 at the last step to include the sub-range[lastL ... R].Is that correct?
Can someone explain this line from the editorial? dp[i][l]=dp[i−1][dp[i−1][l]] since 2^(i−1)+2^(i−1)=2^i.
$$$dp[i][l]$$$ = the index which you reach by moving $$$2^i$$$ indices to the right of index $$$l$$$.
Also, $$$2^{i−1}+2^{i−1}=2\cdot2^{i−1}=2^{i−1+1}=2^i$$$
This means that if you first move $$$2^{i−1}$$$ indices to the right of index $$$l$$$ (let this index be called $$$p$$$) and then you again move $$$2^{i−1}$$$ to the right of index $$$p$$$ you end up moving $$$2^i$$$ indices to right of index $$$l$$$.
$$$dp[i−1][l]$$$ is this index $$$p$$$ which I defined above.
So $$$dp[i-1][dp[i-1][l]] = dp[i-1][p]$$$ means move $$$2^{i−1}$$$ indices to the right of index $$$p$$$.
I hope now the dp relation makes sense.
143424733 B problem is very easy to solve in O(N);
Best Egyptian rounds prepared by this guy. The most recent round tho had some good problems ,but messy with weak pretests
O(n) solution for problem B:
A mathematical proof for why just removing one element works in the solution of C- Baby Ehab
Suppose we have an array a1,a2,a3,a4..... an on n elements and suppose this is a good array, so it can be divided in two partitions:
a,b,c,d... and a1,b1,c1......
so that a1+a2+a3+a4 .... = b1 + b2 + b3 + ....
Now if we divide all these elements with some common factor of all these elements, then the equality will still be valid.
This means that both side will still be equal, ie total sum of both sides will still be 2*something, so total sum will still be even.
Suppose there are k elements that have least significant bit, say 2^p
Now if we divide all elements with 2^p ,
we will have (a1/2^p) + (a2/2^p) + (a3/2^p) ..... = (b1/2^p) + (b2/2^p) + (b3/2^p) .......
at this point , those k elements will become odd,
and we have already proved that the total-sum will still be even ,
so odd elements should be even in number ,
which means k=even.
Now from these k, we just remove 1 element that will become odd after dividing by 2^p.
And k will become odd and totalsum will also become odd.
And now we wont be able to partition into two subset with equal sum.
So just removing one element that has least significant set bit would work.
The general takeaway is that if an array has good partition, then if you divide all elements by any of their common factors, the total sum should still remain even.
So, somehow if we can remove elements so that totalsum after division becomes odd at some point , it will no longer be a good partition.