344A - Magnets
By the definition each block consists of a number of consequent and equally oriented dominoes. That means that in places where adjacent dominoes are not oriented equally, one block ends and another block starts. So, if there are x such places, the answer is equal to x + 1.
Solution complexity: O(n). Problem author: gen.
Bonus: The problem was created a day before the contest and filled in the last part of a physically flavoured DivII complect. :]
344B - Simple Molecules
First solution. First, the sum a + b + c should be even, since each bond adds 2 to the sum. Now let x, y, z be the number of bonds between 1st and 2nd, 2nd and 3rd, 3rd and 1st atoms, accordingly. So we have to solve the system x + z = a, y + x = b, z + y = c. Now observe that the solution to the system is the length of the tangents on the triangle with sides of length a, b, c to its inscribed circle, and are equal to 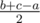 ,
, 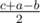 ,
, 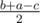 . If the problem asked only the possibility of building such a molecule, we could just check if there exists (possibly degenerate) triangle with sides a, b, c.
. If the problem asked only the possibility of building such a molecule, we could just check if there exists (possibly degenerate) triangle with sides a, b, c.

Second solution. Bruteforce all x values. For a fixed x values of y and z are defined uniquely: y = b - x, z = a - x.
Solution complexity: O(1) / O(n). Problem authors: gen, andreyv.
Bonus: Can you solve the problem for any vertex number n? When and how can such a graph be built?
343A - Rational Resistance
If a fraction  can be obtained with k resistors, then it is simple to calculate that we can obtain fractions
can be obtained with k resistors, then it is simple to calculate that we can obtain fractions 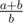 and
and 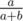 with k + 1 resistors. So adding one resistor means performing one operation backwards in Euclidean algorithm. That means that the answer is equal to the number of steps in standard Euclidean algorithm.
with k + 1 resistors. So adding one resistor means performing one operation backwards in Euclidean algorithm. That means that the answer is equal to the number of steps in standard Euclidean algorithm.
Solution complexity: 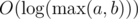 . Problem authors: gen, andreyv.
. Problem authors: gen, andreyv.
Бонус: At first we thought about the major problem (any two elements can be joined), but had a moment of eureka and got that the given problem unexpectedly naturally can be reduced to GCD. By the way, the result tree — http://en.wikipedia.org/wiki/Calkin%E2%80%93Wilf_tree.
343B - Alternating Current
Let us solve the following problem first: we are given a string of symbols A and B. If the i-th symbol is A, then at the i-th step the upper wire (see figure) is being put over the lower wire. If the i-th symbol is B, the lower wire is being put over the upper wire at i-th step. Observe that if some two symbols A and B are adjacent, we can untangle this place, throw the symbols out and obtain the string of length two symbols less. So the wires can be untangled iff the number of A's and B's in the string is the same. The given problem can be reduced to the described in a following fashion: in each odd position we change – to B and + to A. In each even position we change — to A and + to B. The reduction is correct, since on each even position the order of — and + are always swapped, and in each odd position their order is the same as in the beginning.
Solution complexity: O(n). Problem authors: gen, andreyv.
Bonus: If you are interested by this problem, you can learn about the braid theory http://en.wikipedia.org/wiki/Braid_theory :] Fun fact: a harder version of this problem was planned already for Round #142, but the error in solution idea was found, and the problem was left to lay for almost a year.
343C - Read Time
Let's search the answer t with the binary search. Fix some value of t. Look at the first head from the left h[i] that can read track p[0]. If p[0] > h[i], then h[i] goes to the right t seconds and reads all tracks on its way. Otherwise if p[0] ≤ h[i], then the head has two choices:
- go to the right
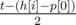 seconds, then
seconds, then 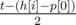 to the left and h[i] - p[0] again to the left;
to the left and h[i] - p[0] again to the left; - go to the left h[i] - p[0] seconds, then h[i] - p[0] to the right and t - 2·(h[i] - p[0]) again to the right.
Obviously, for h[i] it is more advantageous to visit the track positioned as much as possible to the right. So we choose by 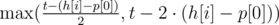 . Then we move the pointer onto the first unread track, and repeat the algorithm for h[i + 1], and so on with each head.
. Then we move the pointer onto the first unread track, and repeat the algorithm for h[i + 1], and so on with each head.
Solution complexity: 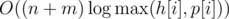 . Problem authors: gen, gorbunov.
. Problem authors: gen, gorbunov.
Bonus: The problem is completely real, if the disk has only a single head, if we know, what tracks should be read; then the optimal algorithm chooses between the two choices described above. I and gorbunov were listening this on a lecture, and created the given problem out of boredom ;]
343D - Water Tree
Let's learn how to color a whole subtree. For that enumerate all vertices in post-order DFS. Then each subtree covers a single continious vertex number segment. For each vertex we store the bounds of such segment for a subtree with a root in this vertex. Then to color a subtree means to color a segment in a segment tree.
Then create a segment tree that has a following property: if a vertex v was emptied, and is still empty, then this vertex is colored in the segment tree. In the beginning "empty" all the vertices. That is, color all the vertices in the segment tree. With this tree we can efficiently process the queries:
Fill a vertex v. Clean the interval for the subtree of v. If before that some vertex of a subtree was empty, color the parent of v.
Empty a vertex v. Color the vertex v in the segment tree.
Reply whether a vertex v is filled. If in the segment tree at least one vertex is colored, then there is such a descendant of v that is empty now, so the vertex v is not filled.
Shtrix noted that essentially the same solution can be implemented with only a single set.
Solution complexity: 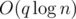 . Problem author: gen.
. Problem author: gen.
Bonus: Some participants could see the similarities with a problem Ball Machine from BOI 2013, but the solutions to the both problems are quite different.
343E - Pumping Stations
In this problem we are asked to find such graph vertex permutation that maximizes the sum of the maximum flows sent between each two consequtive vertices in the permutation.
The problem can be solved with Gomory-Hu tree data structure. For a given weighted graph the tree has the following properties:
- The vertex set of the tree and the graph is the same.
- The maximum flow between vertices u and v in the tree is equal to the maximum flow in the graph.
Surprisingly, such a tree exists for any weighted graph, and can be built in O(n·maxFlow). It appears that the answer to the problem is equal to the sum of the edge weights in this tree.
We prove this statement by induction on the number of the tree vertices. Pick the edge (u, v) with the smallest weight in the tree. Consider that in an optimal permutation more than one path between two adjacent verteces in the permutation passes through this edge. Erase all these paths, then each of the u and v subtrees holds a set of disjoint remaining paths from the permutation. For each set, join all the paths in one chain, obtaining two chains. These chains we join by a path s that goes trough the edge (u, v). Thus we have built a permutation that is not worse than the considered one. For a path s the edge (u, v) is the smallest, so the flow along this path is equal to the weight of this edge. It follows from the induction that in subtrees u and v the answer is equal to the sum of edges. By adding the weight of edge (u, v), we get the desired result.
From the last paragraph it is clear how to build such a permutation: take the smallest edge, obtain two chains from the vertex subtrees recursively, and add them together to form a one chain. Since there are not many vertices, we can do this part in O(n2).
Solution complexity: O(n·maxFlow). Problem authors: gen, Gerald.
Bonus: Shortly before the contest we decided to make the constraints more loyal, so some solution that find Gomory-Hu tree by finding flow O(n2) times also passed. We hope that nobody is particularly saddened by this fact. (;











Hai this was my first round in Codeforces. But my code was not accepted and it says that it was wrong with the 3rd test case. What i did was put a loop from 0 to n-1 and i checked ch[i][!=ch[i+1][0] then count++; else continue where 'ch' is the character array(2-D) whose size was Nx3 ...Is this algorithm completely wrong. As i said this was the first round here i did not understand what is wrong with this. If possible please do tell me what is wrong with this algorithm..:(
Please look at link http://codeforces.me/contest/344/submission/4461494.
The log says
Time: 0 ms, memory: 0 KB Verdict: WRONG_ANSWER Input 1 10 Output 0 Answer 1 Checker comment wrong answer 1st numbers differ — expected: '1', found: '0'
I believe this should be self explanatory.
Also it would help playing around with the system before trying to enter a rated match.
Could somebody please clarify the two choices of head(s) in the solution of 343C-Read Time problem above? I couldn't understand it completely. Thank in advance!
You have to choose one of the two types moving: first to the right or first to the left. You have to use the one which covers more points to the right. Note that both types of moving cover the left point and that's why you have to take as much as points as you can to the right.
Could somebody give me a hint for the bonus at Div2 — B?
Think greedy ;]
will the connections between the atoms be circular? like 1 <-> 2 <-> 3 <-> 4 <-> 5 ... n <-> 1 (again) ?
Can you give a better hint? (Maybe through a spoiler, I suppose)
I think the algorithm that continuously connects the vertex with the smallest degree with the vertex with the largest degree works (here by degree I mean the unconnected edges), and builds a connected graph. I think this can be proved by induction.
I think there is an issue with Problem 343A — Rational Resistance. Here according to the editorial the answer to the ratio 6/5 would be 6(I have verified this with an accepted solution). But this ratio can be achieved with a resistance of 2 and 3 in parallel, which makes the number of resistors required equal to 5 which would imply the editorial and the system tests to be wrong.
Am I missing something here?
I think it's because the definition of one element only let you add one new unit resistor to another element
Thanks for the nice problems!
I just have a little question on 343C — Read Time. I use the same algorithm and get AC, but my algorithm is running at O(n log^2 n)... as for the step: "Then we move the pointer onto the first unread track" I use another binary search...
how can I implement the same algorithm with O(n log n) as said in editorial?
We hold two pointers: the first points at the first unread track from the left, and the second points at the first unused head so far. So we take this head and read with its help the maximum number of yet unread tracks (note that they are consequent and begin at the first pointer) according to the best of the two choices described in tutorial. Then we move the first pointer to the first yet unread track, and increment the second by one. Thus each pointer moves O(n) times in this iteration of the binary search. Take also in consideration that some heads can be not used at all.
Hi. I was just trying to solve problem A of division 2, but was unsuccessful after hours of effort. I eventually lost patience and decided to see the codes of others. I did understand what was going in the code, but couldn't figure out why this method was chosen in the first place. Can someone please help me understand the solution?
P.S. I'm a newbie with almost no prior knowledge about number theory. :$
The number of islands is always one more than the number of splits between two neighboring dominoes. One can easily convince himself by looking at an image in the description.
There are 4 possibilities of neighboring dominoes:
So, we can deduce that we're only interested in neighboring dominoes that are different. This means we can just count the number of indexes i (1 <= i < N) such that s[i] != s[i+1].
I'm confused by the first sentence of 343A — Rational Resistance tutorial
How can we obtain a/(a+b) with k+1 resistors if obatined a/b wiht k resistors ?
Remember a/a is 1. If we have a/b resistance, put one more resistor parallel will give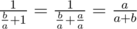
adding one resistor means performing one operation backwards in Euclidean algorithmCan someone explain this ?
gen ?
Suppose you have resistance of(17/3), it could be formed by adding 1 + (14/3). If you have resistance of (3/17), it could be obtained by combining resistance of 1 and 3/14 in parallel.
In terms of variable, a/b could be obtained by 1 + resistors required to create ( a-b)/b resistance, assuming a>b. and a/b if b>a, could be obtained by 1 + resistors required to create ( a/(b-a) ).
Assuming a>b so resistorRequired(a,b) = 1 + resistorRequired(a-b,b).
............
let say r = a-q*b == a%b now at this point, one resistance needs to be connected in parallel to the b/r resistance.
so again problem becomes calculating the requiredResistance(b,r) similar to above problem,
which is similar to the gcd problem.
Hope that helps.
Why it's like gcd(a,b) = gcd(a-b,b) =gcd(a-2b,b) ....
In case of gcd(a,b) = gcd(a-b,b)
Thanks a lot for the nice explanation. Now the use of euclidian algorithm to solve this problem makes sense to me.
Can anyone explain to me the solution for Problem C div2 I understand the transition from
ktok + 1but the part about Euclidean algorithm is beyond mewater tree can be solved by heavy-light decomposition...
Yes, this is almost the most standard problem for HLD. But their solution is cleverer and has lower time complexity. HLD is a little bit overkill for such simple operations.
Nevertheless, HLD can pass the test. My HLD solution passed in 900ms.
Also HLD was a relatively unknown algorithm to the CP community 5 years ago.
Can you explain how to approach this with HLD? I am new to HLD, and not able to get any clue here.
Thanks
I wonder why I did wrong in the implementation of lazy propagation for Div1D, could anyone kindly lend some help?
http://codeforces.me/contest/343/submission/20226349
Thanks in advance. =)
Accepted solution for the problem 343A Rational Resistance would give 6 as the output for input a = 10 and b = 7 i.e.10/7. But, if we have 5 ohm and 2 ohm resistors in parallel, then we have the same resistance value 10/7. So minimum value should be 2 resistors for this case. Kindly explain if i am wrong in understanding the problem?
You have only 1-ohm resistors in the beginning. Thus it requires 5 1-ohm resistors to make a 5-ohm resistor, and 2 1-ohm resistors to make a 2-ohm resistor. So according to you answer is 7 and not 2.
In 343D — Water Tree query 1 and 2 can be solved using a dfs to find in time and out time for every node and then using segment tree But what about 3rd query how to solve it??
yeah same question .
Q.343A can anybody explain me why min resistor for 199/200 is 200.....it can be also constructed using 101 resistors(1/2+1/4+1/5+1/40+1/50)
correct!!!
It is because they are separate elements and hence they cannot be added together. Only an element and a 1 unit resistance can be added in series(or parallel)
Thanks
An alternate approach for solving D: Use of lazy segment tree over HLD & Euler path. For every filling, fill Euler path with current query number, and for emptying, fill HLD path from the root with query number. For queries, check which of the seg tree has high query number.
Problem 344A
This is my code, but I don't know how to improve it, so that the time limit won't be a problem anymore. Any help?
You can make two variable for prev and current value and if they are not equal you can increment it.
In Problem C, if more than one of the elements can be in parallel than for ratio 199 and 200 the answer given is 200. But we may solve this in 74. like 1/2+1/4+1/8+1/10+1/50.
Okay it would be like either + denominator to the numerator or + numerator to the denominator.
gen or andreyv or can anyone please explain
Alternating CurrentSolution.Tried so hard but not able to understand it. ATry it using stack