Today at 11:00 AM EDT will SRM 585. Lets discuss problems here after end of the contest.
→ Pay attention
Before contest
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
16:56:41
Register now »
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
16:56:41
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | djm03178 | 152 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/30/2024 00:38:19 (l1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Updated compilers and added Python compiler!
But they failed to provide it during contest time. Hope good luck for next time.
I coded in c++ and have +220. Feeling WOW!!
(ignore)
Who can't see pictures?
UPD: fixed, sorry.
In Div1 250 the answer is [(2^(N+1)-1)/3] +1*((2^(N+1)-1) % 3 !=0). However everybody in my room got something like dp solution. What's the logic of dp solution here?
It is easy to see that you need send car from left leaf to second left, from third left to fourth left, and so on. So, two bottom levels are removed, and repeat.
UPD: And so we have something looks like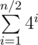
I had the same thoughts, but derived formula instead of doing easy calculation with arrays :(
Yeah, I did the same. That was my quick idea I got from the example tests' pictures.
its dp[0]=1; dp[1]=1; for all i=2 to n dp[i]=dp[i-1]+2*dp[i-2];
its Jacobsthal sequence sequence http://oeis.org/A001045
Alternatively:
If you run one car from the leftmost leaf to the rightmost leaf of the tree, what's left is a sequence of pairs of smaller trees with heights 0,1,..,treeHeight-2.
When I run applet it always unable to launch. I go to topocder but the page can't be access. I can only launch applet at half of contest and in challenge phase I was kicked out of applet. Anyone tell me it topcoder's error or my network's error?
oeis is your friend as well :)
same here I used OEIS :)
can someone explain how to solve DIV2 1000?
step 1 . choose 3 color
step 2 . choose 1 point for each 3 color O(n^3)
step 3 . check them . if this triangle covers black points increase ans ;
in step 3 if u dont know how to check any point is inside the triangle trick is if any pair of points in triangle (p1,p2) if ccw(p1,p2,p3)!=ccw(p1,p2,point) point is outside else inside
more eficient way is choose 2 points and use binary search for 3.point or another way is for each pair of colors find pair of points that not divides black points O(n^2)
Do you mean that complexity of your solution is O(number_of_black_points * m^3) ?
no there is a paragraph that explains eficient solution.
can you plz expalin this condition : ccw(p1,p2,p3)!=ccw(p1,p2,point) What is CCW ?
CCW means counterclockwise.
ccw(p1,p2,p3)!=ccw(p1,p2,point) means that the arcs p1-p2-p3 and p1-p2-point do not rotate in the same direction.
Here is another algorithm in O(MMN). I observed that for all valid triangles, two of the three pairs of the vertices are chosen from the two perpendicular sides of the M*M square. Thus we can count them by going through all pairs of the two vertices on the sides colored (R, G), (G, B), (B, Y), (Y, R). For each pair, we can check if it can contain all the points in O(N) and also count the number of the possible third vertices in O(lgM) by using binary search to find the boundary of the possible third vertices on the other two sides of the M*M square. So in the end, the total needs to be divided by 2, because we double count each triangle.
Div 1 500 was a quite interesting DP. Unfortunately I couldn't fix my bug in time (2 lines misplaced T T).
Help me please. I was participating from my PC, but then electricity fell down. I took laptop, but arena wasn't working on it. It says "Unable to launch the application". What is the reason of problem?
Yesterday I had the same problem. I've cleaned java cache (found this tip at topcoder forum).
Nice problems ! :D
I'm not sure, but I think another recursion that could be found is an = 2n - 1 + an - 2. It gives the same result as the other recursion.
My approach to find this recursion was to use one car for each of 2n - 1 binary trees of height 1 at down of tree, so the tree without them would be a binary tree with height of firstHeight - 2.
Can someone mention the idea behind using Jacobsthal sequence in this problem, or it's just a consequence?
Editorial