Квалификационный раунд и его разбор были подготовлены Chmel_Tolstiy, aropan, Romka, SobolS, Ra16bit, snarknews и Gassa.
В квалификационном раунде турнира Яндекс.Алгоритм стартовало виртуальный контест 1732 участника, хотя бы одну попытку сделало 1606 участников. Из них 1558 решили хотя бы одну задачу. Отметим, что количество зарегистрировавшихся для участия в турнире — а это 3397 участников — практически вдвое превосходит количество участников, стартовавших контест. С чем это связано — непонятно.
Так как квалификационный раунд проводился в виде виртуального контеста, то участники могли выбрать наиболее удобное для себя время. Наибольшее количество участников онлайн (около 280) было в момент старта раунда, наименьшее — в районе между 3 и 4 часами ночи по Московскому времени (около 20 участников).
Первым хронологически все 6 задач сдал Scott.Ai из Китая; при этом все задачи были сданы «в открытую». Стартовавший почти в 22:00 по Москве i.metelsky (Иван Метельский, Беларусь) сдал задачи A-D «втёмную», E «в открытую» со второй попытки и F «в открытую» с первой и возглавил таблицу с очень неплохим результатом. Однако стартовавший через 4 с половиной часа vepifanov (Владислав Епифанов, Россия) сдал «втёмную» A, B, C, F и «в открытую» D и E с первой попытки, выйдя на первое место по штрафному времени. Уже во вторник утром первую строчку захватывают чемпионы мира из СПб НИУ ИТМО: сначала eatmore (Евгений Капун, победитель финалов ACM ICPC 2009 и 2012), стартовавший около 11 утра, сдаёт все 6 задач «втёмную»... но и он находится на этой строчке всего несколько часов: с той же стратегией, но с лучшим временем его обходит действующий чемпион мира tourist (Геннадий Короткевич, Беларусь). Через сутки после старта квалификации первая тройка выглядит так: Короткевич — Капун — Епифанов. При этом Геннадий Короткевич занял второе место в тестовом раунде, Владислав Епифанов — третье. А победитель тестового раунда — Антон Лунёв (Украина) — стартовал уже ближе к концу времени квалификации. Он сдал «втёмную» задачи A, B, F, D, затем сдал «в открытую» задачу E со второй попытки, затем сдал «втёмную» задачу C и вышел на итоговое третье место, сместив Епифанова на четвёртое. Таким образом, все три победителя тестового раунда оказались в Top4, но в другом порядке. Евгений Капун также получил право участия в отборочных раундах по результатам тестового, так что лучшим из тех, кто ещё не имел права участия в отборочном раунде, оказался занявший в итоге пятое место Иван Метельский. Всего по 6 задач решили 34 участника, при этом наилучший результат участника, сдававшего все задачи «в открытую», — 9-10 место.
Отметим также, что неожиданные затруднения у некоторых участников вызвал тот факт, что в качестве входного и выходного файлов в доступных в системе условиях были указаны stdin и stdout. Некоторые приняли эти обозначения стандартных потоков за имена файлов. В связи с этим жюри приняло решение пересудить такие решения с указанием соответствующих имён файлов; в дальнейшем система в аналогичных случаях во избежание путаницы будет использовать фразы «стандартный ввод» и «стандартный вывод».
Задача A (Древний баскетбольный матч)
В этой задаче требовалось просто сделать то, что написано в условии. Достаточно завести две переменные для подсчёта очков каждой команды и, считывая записи о бросках, увеличивать соответствующую переменную на необходимое количество очков. Узнать, какую переменную нужно увеличивать, можно с помощью оператора if.
Задача B (Простая задача)
Перенесём 1 в левую часть — получим k2 - 1 = p1·p2, или, раскладывая левую часть на множители, (k - 1)(k + 1) = p1·p2. Так как k по условию задачи больше двух, то оба сомножителя в левой части не равны единице, а раз так, то (k - 1) = p1 и (k + 1) = p2 (без ограничения общности считаем, что p2 > p1). Действительно, левая часть должна делиться и на p1, и на p2, то есть если k - 1 = a·p1, а k + 1 = b·p2, то (k - 1)(k + 1) = ab·p1·p2 = p1·p2, так как a и b — целые положительные, то a = b = 1, что и требовалось доказать. Если бы k - 1 делилось на p2, то оказалось бы, что k - 1 = p2, k + 1 = p1, но это противоречит тому, что p2 > p1.
Таким образом, задача сводится к поиску таких k, что k - 1 и k + 1 — простые (так называемые «простые числа-близнецы»; интересно, что задача о том, конечно или бесконечно количество пар таких чисел, в настоящий момент так и не решена).
С предложенными во время тура ограничениями это можно сделать любым способом, даже перебирая все (а не только чётные) k и при проверке числа на простоту перебирая все делители до данного числа. Учитывая, что n ≥ 4, «пустой ответ» невозможен, так как k = 4 удовлетворяет условию задачи.
Ещё вариант — раскладывать k2 - 1 на простые множители и проверять, что таких множителей ровно два.
Задача C (Настольная игра)
Ответ на первый вопрос посчитать очень просто. Это сумма количеств атомов по всем кучкам. Она равна 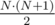 .
.
Для того чтобы ответить на второй вопрос, давайте сперва несколько переформулируем его. Из теории игр известно, что позиция в такой игре является проигрышной, если 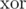 количеств атомов по всем кучкам равен 0. Соответственно, нам нужно найти количество первых ходов таких, что после любого из них
количеств атомов по всем кучкам равен 0. Соответственно, нам нужно найти количество первых ходов таких, что после любого из них 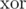 количеств атомов по всем кучкам будет равен 0. Обозначим
количеств атомов по всем кучкам будет равен 0. Обозначим  . Существует быстрый способ посчитать x. Для этого можно воспользоваться фактом, что для любого неотрицательного целого k справедливо
. Существует быстрый способ посчитать x. Для этого можно воспользоваться фактом, что для любого неотрицательного целого k справедливо 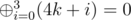 . Значит,
. Значит, 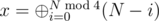 .
.
Если мы зафиксируем номер кучки i, из которой будем производить первый ход, то количество атомов, которые должны будут в ней остаться после этого хода, определяется однозначно. Оно равно 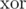 количеств атомов по всем остальным кучкам, то есть
количеств атомов по всем остальным кучкам, то есть  . Значит, чтобы из кучки i можно было сделать правильный первый ход, i должно быть строго больше, чем
. Значит, чтобы из кучки i можно было сделать правильный первый ход, i должно быть строго больше, чем  . Это возможно, только если в позиции p, в которой в числе x стоит старший единичный бит, в числе i также стоит единичный бит. Нужно посчитать количество таких i, не превосходящих N. Среди чисел, меньших
. Это возможно, только если в позиции p, в которой в числе x стоит старший единичный бит, в числе i также стоит единичный бит. Нужно посчитать количество таких i, не превосходящих N. Среди чисел, меньших 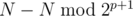 , их ровно половина. Если в p-м бите числа N стоит единица, то нужно также добавить к ответу
, их ровно половина. Если в p-м бите числа N стоит единица, то нужно также добавить к ответу 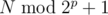 .
.
Задача D (Бесконечная сумма)
Применим несколько преобразований к исходному выражению:
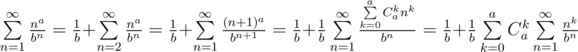
Обозначив 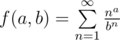 , имеем
, имеем 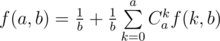
Теперь нужно только посчитать искомое рекуррентное соотношение и вывести ответ.
Задача E (Лабораторная работа)
Случаи X = 0 или K = 0 являются тривиальными и рассматриваются отдельно.
Понятно, что выгодно, чтобы Гена каждый день решал максимальное количество задач, которое может, а остальных студентов можно распределять по темам, и они могут подстроиться под работу Гены. Если в какой-то теме ещё осталось решить не меньше X задач, то Гена в этот день работает на максимум и решает X задач. Если такой темы нет, то он берет тему с наибольшим количеством задач и решает их, полностью закрывая тему. Таким образом, становится очевидным, какое минимальное количество задач останется после Гены по прошествии некоторого количества дней. Тогда можно двоичным поиском перебирать количество дней, т. е. ответ, затем проверять, успеют ли студенты за этот срок решить оставшиеся после Гены задачи.
Сложность такого решения 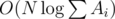 . Также следует учесть, что нужно предварительно отсортировать темы по значению
. Также следует учесть, что нужно предварительно отсортировать темы по значению 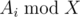 для поиска тем с максимальным количеством задач, когда у Гены уже нет возможности решать по X. Итоговая асимптотика с учётом того факта, что
для поиска тем с максимальным количеством задач, когда у Гены уже нет возможности решать по X. Итоговая асимптотика с учётом того факта, что 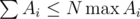 , и свойств логарифма, получается
, и свойств логарифма, получается 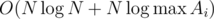 .
.
Альтернативное решение заключается в рассмотрении оптимальной стратегии для студентов. Зная, как оптимально действует Гена, можно предположить, как должны действовать студенты: вначале они должны решать тему с наименьшим значением 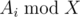 и решать эту тему, пока
и решать эту тему, пока 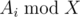 не станет равным нулю. Когда такие темы закончатся, а задачи ещё останутся, то они могут выбирать любую тему и решать её, пока в ней не закончатся задачи. Таким образом, надо рассмотреть что произойдет первым: либо у Гены раньше закончатся темы с Ai ≥ X, либо у студентов закончатся темы с
не станет равным нулю. Когда такие темы закончатся, а задачи ещё останутся, то они могут выбирать любую тему и решать её, пока в ней не закончатся задачи. Таким образом, надо рассмотреть что произойдет первым: либо у Гены раньше закончатся темы с Ai ≥ X, либо у студентов закончатся темы с 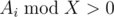 .
.
Сложность 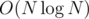 .
.
Задача F (Атомы: туда и обратно)
Количество кучек при каждом разделении удваивается. Из этого следует, что если N не является степенью двойки, то заданное состояние никак не получится и ответ «NO».
Если посмотреть последнее разделение, то есть разделение состояния, предшествующего заданному, то из каждой кучки была получена кучка размера X. Значит, как минимум половина кучек будет одинакового размера X. Тогда эти кучки можно отбросить и перейти к такой же задаче с N / 2 кучками. Если на каком-то шаге среди кучек нет хотя бы половины одинаковых, то ответ «NO».
Для решения задачи можно сгруппировать заданные кучки по размеру. Затем можно, используя кучу (приоритетную очередь), просимулировать вышеописанный процесс. Также можно жадно разбивать каждую группу одинаковых по размеру кучек на кучки, размеры которых являются степенями двойки, так, чтобы каждая степень получилась ровно один раз, кроме нулевой степени (с нулевой степенью должно быть две части).
Сложность 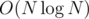 .
.













Прошу прощения за формализм. Задача D — никаких обоснований перестановки слагаемых в ряде, не говоря уже об иссследовании на сходимость. Понятно, что тем, кто знает матан, это в данном случае очевидно, но для остальных следовало хотя бы ссылочку на базовые сведения о рядах оставить.
Приведу ссылки, если кому все еще нужно. Можно поюзать признак Даламбера, чтобы доказать сходимость ряда при b > 1. Потом пригодится бином Ньютона. А в чем проблема с перестановкой слагаемых? Достаточно понимать, что означает значек суммы, чтобы понять переход в разборе (в боевых условиях, конечно, сложно, если видишь подобное впервые).
Thanks for the editorial.
In problem C, the proof of "position in such game is losing if XOR of numbers of atoms in all groups is equal to 0 " can be found here
На сайте соревнования есть такая фраза:"Квалификационный раунд теперь доступен для дорешивания и виртуального участия. Результаты виртуального участия не отразятся на результатах раунда." Виртуальное участие имеется в виду как виртуальный контест на КФ? Если да, то будет ли такая возможность с раундами отборочного этапа, в которых не смог поучаствовать?
да, они через некоторое время также будут переведены в режим открытого дорешивания.