Hi, I was trying to solve this problem from a coding test and came up with an O(n^4) solution which goes like first I will precompute the 2-D prefix sums of the entire grid and then for each cell naively Bruteforce for all possible solutions in n^2 operations, It would be great if you can share your insights/solutions for the problem. The contest is over 5 days back you can answer as late as you want until you are assured of this.
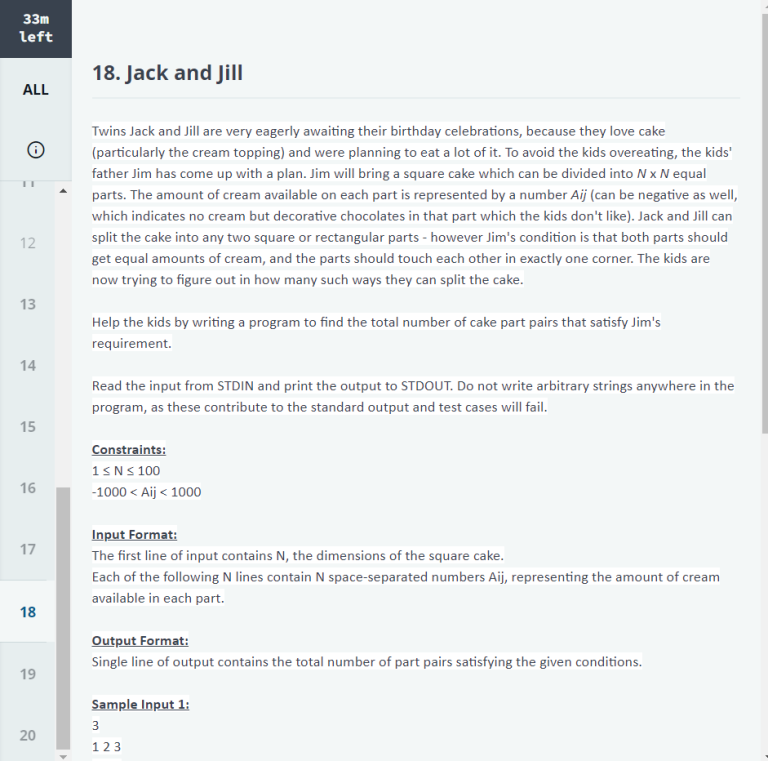
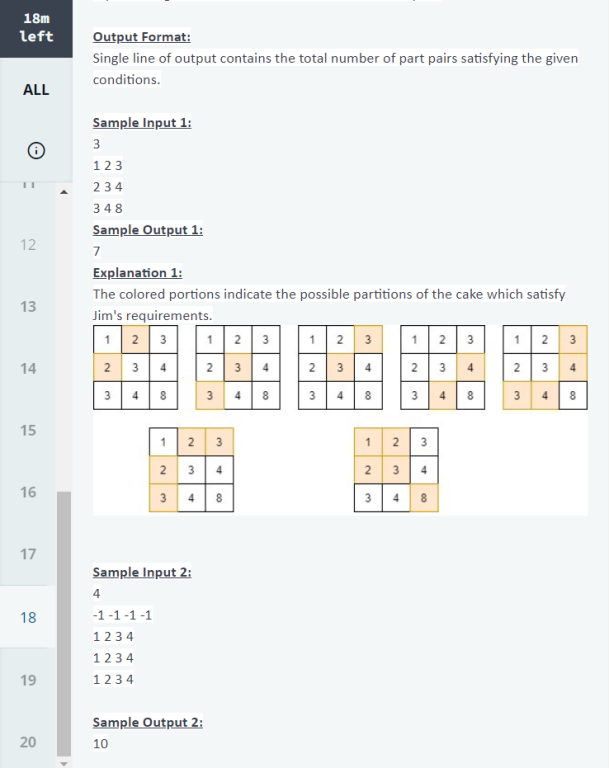
PROBLEM STATEMENT










Seems like it is supposed to be a brute force with 2d prefix sums.
Yes I figured that solution out as I mentioned in the post, please share any better/different solution or approach you have.
On second thought, brute force with 2d prefix sums would be O($$$n^5$$$) right? Because you have to build two rectangles at the same time for each point?
I guess no, as we are just traversing the entire grid for each cell 4 times so it should be O(4*n^4) which is O(n^4) only
Why would not $$$O(n^4)$$$ pass?
Actually I was not able to implement this solution in time, that's why I asked for an approach or solution that is somewhat easier to implement and also if the solution that I suggested in the blog is the desired/correct one or not