iynaur87's blog

A physical proof of Educational Codeforces Round 90 problem F.
By iynaur87, history, 4 years ago, In English

Problem: https://codeforces.me/contest/1373/problem/F

We will prove it is not possible if

  1. total capacities of the designed stations is smaller than total households of all cities. or
  2. for some continuous k stations, their total capacity is smaller than total households of (k-1) cities between them.

otherwise, it is always possible.

It is obvious that if condition 1 or 2 is met, it not possible. Now we prove it is the only senario that it is not possible.

Let us consider a circle segmented to n arcs with n nodes N1, N2, ... Nn. the length between Ni ans Ni+1 is ai(the number of households in the i-th city.) and there is a small ring in arc_i, note as Ci. the rings constrained by its node boundaries. For example ring C1 cannot move outside the bounds of N1 and N2. there is a rope with origin length bi between Ci and Ci+1. the rope can be stretched if necessary.

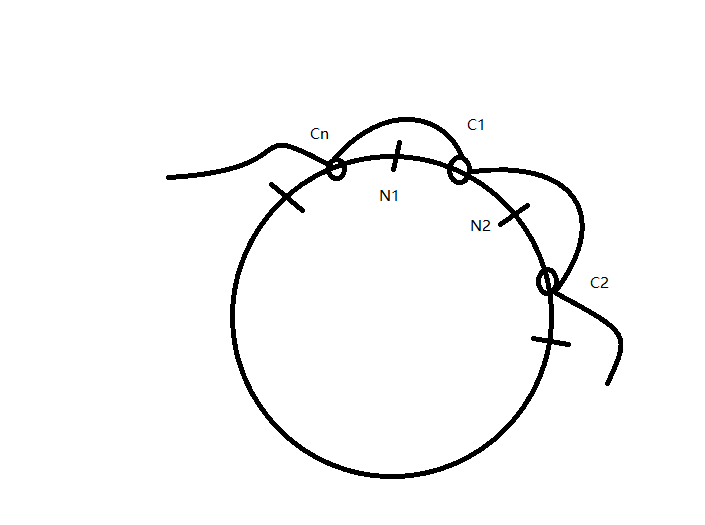
Now if we can arrange all the rings so that no rope need to be stretched, there is a solution.

We just let all rings move freely. if no rope are stretched, it is ok. If some ropes are streched. there are 2 conditions:

a. all ropes are streched, it is condition 1; b. some continuous ropes are streched, while the rope before and after them are not. In this case, the start and end ring of these ropes must be at the node. so it is condition 2.

end of proof. Sorry for my poor English.

  • Vote: I like it
  • +183
  • Vote: I do not like it

»
4 years ago, # |
  Vote: I like it +11 Vote: I do not like it

Are the rings constrained by its N boundaries? For example ring C1 cannot move outside the bounds of N1 and N2?

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Yes, sorry for the confusion, I will edit my blog accordingly.

    → Reply
»
4 years ago, # |
← Rev. 2   Vote: I like it +49 Vote: I do not like it

My favourite physical proofs include this one:

Problem: You are given a solid polyhedron, prove that there exists a face of it such that projection of polyhedron's center of mass to the plane containing that face lies within that face.

Proof: Put this polyhedron on a table. If it is false then it will indefinitely fall over to some other face than one it is currently standing at.

Other example I love is proving some complicated inequalities by showing two electrical circuits with electric resistors such that one circuit has superset of connections of the other one (and they have same resistors), so its resistance must be at most the resistance of the second circuit's resistance.

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it +37 Vote: I do not like it

    That physical proof doesn't work if the polyhedron isn't convex. It might fall to a non-face.

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Is the property still true for non-convex polyhedra? I can’t come up with a break case mentally, but I have no reason to think it would be true...

      → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Only if it doesn't have holes, I think.

        → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        Fortunately (for the sake of physic proof) it is false! You can imagine a thin horseshoe-like polyhedron. If it is positioned horizontally and it doesn't have more or less vertical faces (easy to satisfy) then it will be a counterexample!

        Xellos good catch

        → Reply
»
4 years ago, # |
  Vote: I like it +26 Vote: I do not like it

I was requested to provide an example of proving inequality by electric circuits, so here it is:

We are measuring resistance from S to T. There are four resistors with resistance $$$L, R, U, D$$$ as in the picture. Green connection is present in second circuit only.

In the circuit without green connection we can calculate the resistance as $$$\frac{1}{\frac{1}{L+U} + \frac{1}{R+D}}$$$.

In the circuit with green connection calculating resistance may be a bit more tricky, but we can think that if we contract green wire we have two sequentially connected circuits which consist of parallel connection of two resistors. Hence its resistance will be $$$\frac{1}{\frac1L + \frac1D} + \frac{1}{\frac1U + \frac1R}$$$.

Resistance in the second case cannot be bigger (since adding a connection may not increase resistance) hence we get an inequality:

$$$\frac{1}{\frac1L + \frac1D} + \frac{1}{\frac1U + \frac1R} \le \frac{1}{\frac{1}{L+U} + \frac{1}{R+D}}$$$

(which is true for positive real numbers).

Disclaimer: Such physical proofs may obviously be not accepted as valid mathematical proofs (in competition or research papers). But they are fun.

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    is since adding a connection may not increase resistance because currents will be more divided, so sum of currents emnating from S will be less for the same applied voltage.

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it +29 Vote: I do not like it

      I am definitely not a physical expert (I completely stopped caring about physics when I was ~17 years), but what I remember I was told is that electrons always know what is the best way of travelling for them (collectively, not individually). By adding a connection we just increase their possibilities, so in "the worst case" they can pretend this connection doesn't exist.

      → Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    "Such physical proofs may obviously be not accepted as valid mathematical proofs." But I think we can transport it to valid mathematical proofs using the equations behind the physical principle.

    → Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    A great way to think about circuits with an added short wire is to imagine that instead of 1 source and 1 sink, there are 4 such exits for current, the 2 new ones are "added wire from one side" and "added wire from the other side", with an additional constraint that the sum of currents flowing into them is zero and sometimes also the condition that potentials at the endpoints of the new wire are equal. This sometimes lets us formulate and solve a system of equations that gives the resulting current flowing through it only using properties of the original circuit. Example problem, no physics needed with this trick.

    → Reply
»
4 years ago, # |
← Rev. 2   Vote: I like it +8 Vote: I do not like it

I am sorry if its wrong but Is it true that its similar to Hall Theorem for graph. If we draw $$$a_i$$$ nodes for one city and $$$b_i$$$ nodes for one Network Hub and connect all node of $$$i$$$ hub with $$$i$$$ and $$$i+1$$$ city (and last hub to $$$n$$$ th and $$$1$$$ st city nodes), we need to find matching?

Hall theorem asks us to check for each subset of Set of Cities with $$$x$$$ nodes they must be connected to $$$\ge x$$$ nodes in Set of Network Hub.

Also I am not able to reduce it to the condition 2 in blog, I mean it is necessary but why sufficient

→ Reply