Всем привет!
Меня интересуют два вопроса:
Первый: Как вы генерируете случайную перестановку? Я обычно беру перестановку 1,2,3..N, а потом О(N) раз свопаю рандомную пару. Насколько хорош этот метод и есть ли другие?
Второй вопрос: Как выбрать случайно подмножество размером К из N элементов за О(K)? Если за О(N), то можно ведь ответить на первый вопрос, а потом взять первые К элементов, да?:)
Ответ на первый вопрос: метод плох, перестановки выходят неравновероятные. См. задачу с последнего петрозаводскго Andrew Stankewich contest :-) Вкратце — перестановки с большим количеством циклов в разложении будут гораздо менее вероятны, чем с меньшим.
Правильный способ — на i-ой итерации свапать i-й элемент с рандомным из префикса перестановки длиной i. Если предположить, что префикс длиной i-1 был случайной перестановкой, то легко понять, что после такой операции и префикс длины i будет случайной перестановкой, т. е. всевозможные его перестановки будут равновероятны.
А вообщем, это все реализовано, если кто не знает, в функции random_shuffle из библиотеки algorithm.
Ответ на второй вопрос — за O(N) метод правильный. За O(K) выделять случайное сочетание размера K из первых N натуральных чисел я умею только с помощью какого-нибудь декартова дерева и бинпоиска по ответу (выходит аж O(K log N log K)), но более чем уверен, что можно проще. Можно ведь?
У первого даже есть свое название и хорошая статья на википедии. Еще есть вот такое с наших викиконспектов: Метод генерации случайной перестановки, алгоритм Фишера-Йетса
По поводу второго вопроса:
Выглядит очень хорошо) А после многократного использования перестановка А все еще будет рандомной?
Честно говоря не понял вопрос) Что вы имеете ввиду? Давайте я расскажу откуда это взялось, может это ответит на ваш вопрос.
Рассмотрим вот такую задачу:
Имеем массив размера n. Нам нужно выбирать оттуда какой-нибудь случайный элемент, при этом каждый раз новый (если взяли на шаге x элемент Ax, то на шаге y > x, элемент Ax мы точно не возьмем).
Ну и вот эта задача решается кодом выше.
Разъясните, пожалуйста, подробнее суть вопроса.
Решение нужно было за О(К), то есть предполагается многократное использование. В этом коде нужно каждый раз заново генерировать массив А. Вопрос был такой — останется ли полученный результат по-честному случайным, если этого не делать?
В крайнем случае, можно запомнить все О(К) изменений памяти и потом откатить их назад :)
UPD: ну и ясно, что порядок элементов вообще ни на что не влияет, так что можно ничего не откатывать.
Если примем, что изначально массив А пошафлен, то выборка к-подмножества по всей видимости сгенерирует другую случайную перестановку (перестановки похожи, но специфика задачи это позволяет), а значит на следующей выборке мы имеем исходную ситуацию. Конечно, это не похоже на строгое доказательство, но явного левака я не вижу. То есть для себя я это понимаю, как то, что мы вибираем случайно к-подмножество и это не приводит массив А к какому-либо определенному виду, а значит последующая выборка к-подмножества тоже будет случайна. Пойду попробую построже все рассмотреть.
Во понял. Пусть массив A — изначально случайная перестановка. Тогда сделаем выборку к-подмножества. Теперь рассмотрим то, что мы сделали в обратном порядке. Получим алгоритм, описанный Zlobober выше. А на ту штуку есть строгое доказательство) Следовательно после проделанных операций получим новую случайную перестановку, а значит следующая выборка к-подмножества тоже будет случайной
UPD. И такой способ вообще никак не влияет на случайность, он влияет только на то, чтобы не брать элемент, который мы уже брали -> как написал KADR нам вообще пофиг на порядок элементов в массиве A
Fisher–Yates shuffle можно делать как бы «с двух сторон».
В одном случае, на k-м шаге выбирая случайную позицию из первых k и меняя с ней k-й текущий элемент местами — как у Zlobober — получается случайное перемешивание префикса длины k.
В другом случае, на k-м шаге выбирая случайную позицию из последних n - k + 1 и меняя с ней k-й текущий элемент местами — примерно как у Avitella, но с другими индексами — получается выборка k случайных элементов из n.
Оба варианта при k = n просто генерируют равномерно распределённую случайную перестановку (если считать, что мы пользуемся идеальным генератором случайных чисел).
В обоих случаях количество различных вариантов работы алгоритма ровно такое, как количество возможных ответов (перестановки префикса или выборки без повторения). Несложно доказать, что разные варианты работы приводят к разным ответам. Поэтому все возможные ответы получаются ровно по одному разу, а значит, равновероятны. Причём независимо от исходной перестановки — то есть можно повторно запустить любой из этих алгоритмов, ничего не возвращая на место.
А можно дать ссылку на задачу? Это просто правила приличия, чтобы задача не оказалась с соревнования. Если такой возможности нет, то указывайте хотя бы ограничения на входные данные. При достаточно небольшом X это динамика описанная выше. При большом X и небольших A, B или достаточном количестве запретных чисел, это Meet in the middle, также уже объясненный выше.
На какую задачу? Не тот пост прокомментировал, что ли?
Да. Достал уже этот редирект на рандомную страницу после логина. Ну на самом деле не рандомую, а ту что ты последней открыл в браузере. Но все равно достало.
Думал, но не придумал: а как ответить на второй вопрос — выбрать K из N элементов за O(K) — если нельзя портить исходный массив? Видимо, за
времени и O(K) памяти это делается деревьями отрезков или Фенвика, но хочется проще и быстрее.
Если под "нельзя портить" подразумевается "можно менять, но в конце вернуть в изначальное состояние", то тогда мы можем за те же O(K) операций откатить массив в изначальное состояние после того, как мы выбрали нужные нам K элементов.
Если даже менять нельзя, то можно за O(KlogK) времени и O(K) памяти с обычным map решить или даже за O(K) времени с hash_map. Для этого мы будем все числа, стоящие на позициях, которые мы бы хотели поменять в массиве, хранить в этом самом map, а все нетронутые числа — в изначальном массиве. Тогда при обращении к определенной ячейке массива мы сперва смотрим в map, а уже потом в сам массив. Ну и затем обновляем map соответствующим образом.
Можно даже еще проще: храним все в сете все выбранные на данный момент элементы. Выбираем случайный элемент от 1 до N, и, если мы такой уже брали, повторим выбор, и так далее. Матожидание количества таких выборов до успеха при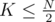
не больше, чем 2.
Да, с матожиданием действительно всё хорошо. Но тут тоже set — TreeSet за
в сумме или HashSet, константы которого всё-таки хочется избежать. Попробую формализовать это требование: как решить задачу, не используя хеши?
Можно положить в массив первые K элементов, проходить по оставшимся, начиная с K + 1, и на i-ом шаге с вероятностью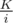
заменять случайный элемент из массива i-ым.
Если пройти по всем оставшимся элементам массива, то получится O(N) времени, чего хочется избежать. А хочется O(K) времени и памяти. Это важно, потому что K может быть много меньше N.
К тому же это решение равномерно вытаскивает K элементов, но неравномерно их перемешивает: например, если K = 2, может получиться
1 2, но не может2 1. Но это не страшно: K элементов за O(K), если нужно, уж как-нибудь перемешаем любой вариациейrandom_shuffle.Вообще, идея забыть для начала про равномерное перемешивание мне нравится, спасибо! Осталось понять, не получится ли «ужать» эти O(N) в O(K).
Если первым K элементам сделать
random_shuffle, то и в конце перемешивание будет случайным.Памяти O(K); более того, массив можно из файла читать, к примеру.
Насчет времени: казалось бы, массив надо прочитать, это уже O(N). Если надо несколько случайных подмножеств одного множества, можно генерить их все на одном проходе. Других юзкейсов решения за O(K) я придумать не могу.
А вообще, выбор случайного подножества (даже без перемешивания) подразумевает генерацию как минимум
(при K = o(N)) случайных битов, так что вряд ли тут что-то получится придумать.
Use case: в памяти лежит массив (или другой O(1)-random-access контейнер) размера N = 100000. К нему из разных тредов обращаются с запросами «дайте нам K случайных элементов без повторений», распределение должно быть равномерным с учётом порядка, K = 50. Запросы нужно обрабатывать в реальном времени за O(K) времени, используя O(K) памяти.
А сколько всего максимум тредов? И что еще происходит с контейнером помимо обращений тредов к нему?
Тредов сколько угодно. Контейнер можно считать, что
constкусок памяти.А что хочется делать с контейнером? Сомневаюсь, что получится сделать какой-то полезный предподсчёт, чтобы он был один для всех тредов.
Тогда я не до конца понимаю. Хочется реализовать некую структуру данных, которая умеет потокобезопасно возвращать выборку к-элементов из нашего контейнера, при чем контейнер не изменяется, то есть в него ничего не добавляется и из него ничего не удаляется? Разъясните, пожалуйста, подробнее. Просто в вашей постановке проблемы непонятно, откуда может взяться сколь угодно тредов.
UPD. Почему нужно делать выборку именно за О(К) (при таком маленьком К)?
==================================================================
В памяти растут N = 100000 клумб с цветами. Неизвестное количество тредов-цветоводов делают из этих цветов букеты. Каждый цветовод хочет, чтобы аппаратура сада за O(K) выдала ему равномерно распределённое случайное размещение из N элементов по K, после чего проходит по таким клумбам в таком порядке, срезая по одному цветку и получая размещение-букет.
Здесь каждая клумба — это не
constзначение, а объект, который при доступе к нему треда может что-то внутри себя сделать: например, отдать один цветок, запомнить цветовода и так далее. В таком случае размещение, которое нужно выдать — это K указателей на объекты (а не копии объектов). Мне кажется, нет разницы, решать ли задачу для массива констант или для массива сложных объектов, а такая постановка может быть понятнее. Всё равно по сути нам нужно K чисел от 1 до N без повторений, сделать из них указатели можно за те же O(K).UPD. Почему нужно делать выборку именно за О(К) (при таком маленьком К)?
В идеале садовнику хочется не заранее выбрать K и сразу получить всё размещение, а более лениво: выбирать каждый следующий цветок без повторений онлайн за O(1), хотя бы амортизированные, и остановиться, когда захочется. Это чуть более сильная формулировка, но я пока даже для слабой не умею решать.
================================================================== А если делать что-нибудь типа такого. Функция принимает аргументы: выбрать из подотрезка от L до R K-элементов, а возвращать будет количество элементов, которые удалось взять. Берем изначально элемент на случайной позиции M. Теперь нужно добрать элементов от L до M — 1 и от M + 1 до R. Сделать это видимо можно, если разбивать (K — 1) на K1 и K2, где K1 / K2 пропорционально (M — 1 — L) / (R — M — 1). Встает вопрос о случайности сего действия. На самом деле даже кажется, что это не совсем неверно. Тогда еще идея: бить (К — 1) на К1 и К2 некоторым случайным образом. Но тогда непонятно, что делать, если на текущем подотрезке мы не можем добрать нужное нам К (UPD. и встает вопрос о равномерности сего способа).
P.S. Так, мысли вслух. Интересно, похоже ли это на что-то нормальное, или совсем бред.
UPD. Видимо можно попробовать так. Даже не пробовать, потому что очень похоже на правду. Требуется О(К) памяти + О(1) на запрос. Имеем массив из К пар, то есть будем в ячейке хранить отрезок (начало и конец), из которого будем выбирать элемент. Сначала там лежит только один элемент — (0, N). На i-ом шаге берем случайный элемент нашего массива пар (удаляя его, соответственно). Выбираем случайный элемент в этом отрезке. Отрезок побился на два (от начала отрезка до выбранного элемента и от выбранного элемента до конца). Вставляем эти два отрезка в наш массив (видимо, можно даже просто вконец). Размер массива в худшем случае увеличился на 1 => он не превзойдет К. Вроде все хорошо получается.
UPD2. Я даже осмелюсь утверждать, что это верно. Потому что по сути, на каждом шаге мы просто выбираем случайную позицию в исходном массиве, так как мы берем случайный отрезок + случайный элемент => и позиция в исходном массиве случайна. Мы просто точно не возьмем элементы, которые мы уже выбирали. Неверно
====================================== Кусочки массива будут в результате разной длины, поэтому когда мы случайно выбираем кусочек, а потом случайно выбираем элемент в нем, нельзя сказать, что мы случайно выбираем элемент. Пример — если K = 2 и первым ходом мы выбрали i=2, то вторым ходом мы с вероятностью 1/2 выберем элемент с i=1, что, очевидно, неправильно. Условная вероятность не та.
=============================================================
В таком решении, чтобы получилось равномерное распределение, нужно выбирать каждый отрезок с вероятностью, пропорциональной его размеру, а не все с одинаковой вероятностью.
====================================== А разве мы умеем выбирать элементы не с равной вероятностью, а с заданной, быстрее, чем за логарифм (частичные суммы и бинпоиск)?
Не умеем. Gassa просто сказал чем плохо мое решение.
============================================
Я не умею из этого решения делать O(n). Умею только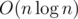
с деревом отрезков или Фенвика, а потом двоичным поиском.
Насчёт битов: мы считаем, что число типа
size_t(например, равномерно распределённое на целых числах из [0, N)) генерируется за O(1). Это вполне реалистичное умолчание. К тому же, если разрешается менять массив, решение существует, и очень простое.Юзкейс: есть массив на сервере, на него поступают запросы от клиентов и нам в реальном времени нужно выбирать подмножество размера К. Тогда оффлайн решения нам не подойдут, равно как и решения за O(N).
UPD: пока думал над второй частью уже на все ответили
Оффтоп: как цэшку в техе нормально сделать?
У меня только вот так получается: CNK. Хотя во всех рендерерах кроме рендерера КФ это нормально выглядит.
Ну, код
C_{N}^{K}попадает к HTML-рендереру, и получается CNK (<span class="tex-span"><i>C</i><sub class="lower-index"><i>N</i></sub><sup class="upper-index"><i>K</i></sup></span>).Более сложный код типа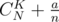
(
C_{N}^{K} + \frac{a}{n}становится картинкой, и получается<img align="middle" class="tex-formula" src="https://espresso.codeforces.com/0ee60dc44fd3846102b4c72dbf97fb54265bf49a.png" style="max-width: 100.0%;max-height: 100.0%;" />).Забавный эффект ещё внутри скобочек, там обратные кавычки, в них доллары, а в них формула.
Да, совсем нельзя менять.
constтам, или многопоточность, в общем, менять и откатывать не следует.Да, hash_map формально будет за O(K), идея с доступом через неё хороша, cпасибо! Но фактически получится сравнимая с
cкорость, а хочется быстрее (и проще: без
constже совсем всё просто)...