Rafat's blog

Help needed to solve a high school geometry problem.
By Rafat, history, 5 years ago, In English

Given the side length of one equilateral triangle and 3 radii R1, R2, R3 which produce 3 sectors inside the triangle. Calculate the area of the triangle which is not covered by the sectors.

My idea is
We can see there can be three cases.

  1. any radius from R1, R2, R3 is greater than or equal to S for which the answer will be Zero
  2. if R1+R2<S and R2+R3<S and R3+R1<S so the answer will be Area of ABC — Area of 3 sectors
  3. if one sector intersects with another...
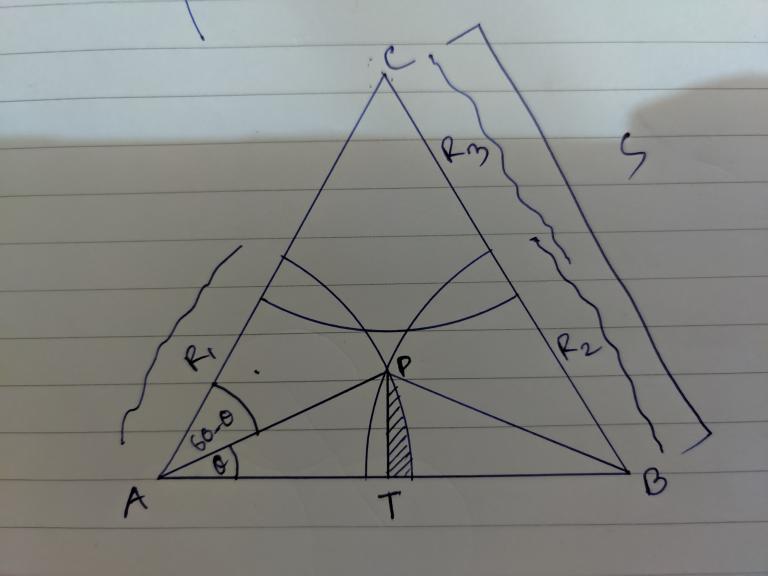
    For this case, I will check if every pair of circle intersects or not. For this let's denote P as the intersection point. and let's draw a line PT which is perpendicular to the line AB. so from triangle APT and the new sector with an angle 60-Theta so I can get the dashed area from Previous sector Area — (new sector area + triangle APT). with same this approach, I can get the opposite dashed area too which is calculated twice in the addition of sectors area since they intersect. So I'll subtract it from the original sector area.

I'm getting WA with this approach. can you please help me find my mistake :) I'll be glad.
My solution
Problem Link (Problem J)

you can submit your solution for this problem here to check if it gets AC Judge

  • Vote: I like it
  • +22
  • Vote: I do not like it

»
5 years ago, # |
← Rev. 3   Vote: I like it +2 Vote: I do not like it

I'm not sure why it happens, but your code doesn't work on this sample:

1

100 98 1 1

I'm guessing something to do with the biggest circle going out of the triangle?

→ Reply
  • »
    »
    5 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    thank you. I didn't notice this case! any idea to handle this case? I edited my solution for this case. still getting WA. This is the new solution. added line 19-36 for this case

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
      ← Rev. 3   Vote: I like it +2 Vote: I do not like it

      Now it doesn't work for

      1

      100 98 50 1

      I think it's a problem when you calculate the area of intersection for 98 and 50 you count some area outside of the triangle. Good luck :)

      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Got it but stuck at this point. Don't know how to go further :(

        → Reply