Вот такой вот продукт отечественного юморка получился в результате подготовки вместе с GShark и zakharvoit к открытой московской олимпиаде. 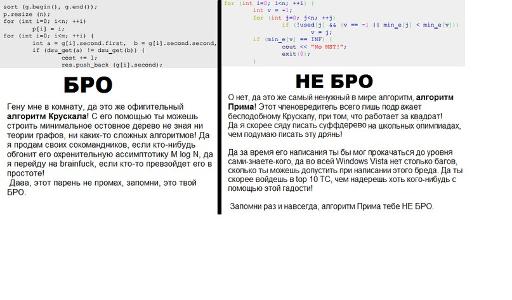
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
00:08:17
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
00:08:17
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 17:26:43 (h1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Я просто напишу, что Прима можно несложно написать за M+NlogN и совсем легко(особенно на С++) за MlogN.
И да, кстати, в Краскале сортировка за MlogM.
Короче, я всегда считал, что это довольно схожие алгоритмы и выбор между ними — вопрос вкуса.
А я их вообще не различаю:(
Пишу что-то, оно каркас находит — и ладно.
Когда-то запутался в этом — прочел об алгоритме Прима, алгоритме Крускала, алгоритме Прима-Крускала... Некоторые авторы еще что-то оригинальное придумывают и называют одно и то же разными именами...
И я решил не забивать себе мозг:)
О(m * log(m)) и O(m * log(n)) здесь одно и то же т.к. m < n^2
Если число рёбер близко к N^2, то алгоритм Прима будет асимптотически быстрее ;)
Петросян, ты готов к олимпиаде.
Спасибо, тренер. А вообще — враки, мы так не готовимся.
Ну насчет бро — не бро не знаю... Может я криворукий, но Крускала здесь запихнуть не смог. Спас меня только Прим.