Блог пользователя 7Midav7

Opencup
Автор 7Midav7, 12 лет назад, По-русски

Подскажите, как решать J и O с недавнего раунда opencup? И какое впечатление у вас оставили остальные задачи?

  • Проголосовать: нравится
  • +3
  • Проголосовать: не нравится

»
12 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Условия в студию :)

→ Ответить
»
12 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Задача О. Число 0 у нас встретится N + 2раз , число 1 столько же, ... число N — тоже. Тогда общая сумма чисел N * (N + 1) / 2 * (N + 2) Значит, в каждой строке будет стоять сумма N * (N + 2) / 2

Построим двудольный граф: левая доля — доминошки, правая доля — строки. Проведем от каждой доминошки к каждой вершине правой доли ребро с пропускной способностью, равной сумме цифр на доминошке. От истока проведем ребро к каждой доминошке с такой же пропускной способностью, а от каждого ряда(вершины правой доли) — ребро к стоку с пропускной способностью N * (N + 2) / 2.

Запускаем максимальный поток. Так как по условию получить результат всегда возможно, то в результате получим полный поток в графе. Тогда для каждой вершины правой доли смотрим какие доминошки отдают поток в нее и выводим.

→ Ответить
  • »
    »
    12 лет назад, # ^ |
      Проголосовать: нравится +8 Проголосовать: не нравится

    Но ведь может получиться так, что из какой-то доминошки поток разделится и пойдет в 2 строки сразу.

    → Ответить
  • »
    »
    12 лет назад, # ^ |
      Проголосовать: нравится +1 Проголосовать: не нравится

    Не слишком богат временем, поэтому вкратце расскажу идею решения задачи O.

    Несложный вывод формул дает понять, что в каждом ряду сумма должна равняться . Каждая кость домино полностью лежит внутри одного ряда, следовательно важно только количество костей домино с каждым из значений суммы от 0 до 2·N. Самым тривиальным алгоритмом эти количества и посчитаем, после чего увидим интересную картину — количества образуют следующую последовательность: 1, 1, 2, 2, ..., , ..., 2, 2, 1, 1.

    Пусть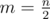 . Тогда возьмем m первых четных чисел и сольем с m последними:

    0 с 2·n - 2·(m - 1)

    2 с 2·n - 2·(m - 2)

    ...

    2·(m - 1) c 2·n.

    Таким образом мы получили m первых строк. Останутся только нечетные суммы и значение суммы n, которые образуют еще более интересную последовательность: 1, 2, ..., , ..., 2, 1.

    Для n mod 4  =  2 имеем следующее решение. Просто будем сбегаться двумя указателями с двух краев и группировать пока сумма не станет равна . Все противоположные пары в сумме дают ровно . Причем в таком случае левая граница может совпадать с правой для значения суммы равного n — попадает под общий случай.

    Для n mod 4  =  0 решение аналогично, только группируем до тех пор, пока сумма не станет равна , после чего добавляем недостающее значение n из середины нашей последовательности.

    Итоговая асимптотика O(N2).

    Если есть какие-то неточности, то уж простите — торопился.

    → Ответить
»
12 лет назад, # |
← Rev. 7   Проголосовать: нравится -17 Проголосовать: не нравится

Бред

→ Ответить
  • »
    »
    12 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    на тесте 1 1 1 (из условия) правильный ответ корень из 5, а у вас не так.

    → Ответить
  • »
    »
    12 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    С каких пор параллелепипед стала женского рода?)

    → Ответить
  • »
    »
    12 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

    Бред написал.

    → Ответить
  • »
    »
    12 лет назад, # ^ |
    ← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

    Этот код получил wrong answer 2.

    d1=sqrt((c+b)*(c+b)+a*a)
d2=sqrt((c+a)*(c+a)+b*b)
d3=sqrt((a+b)*(a+b)+c*c)
ans=max(d1, d2, d3);
    → Ответить
    • »
      »
      »
      12 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится

      Если уж на то пошло, и я правильно понимаю, то хотя бы, ans=min(d1,d2,d3), ибо идет он по кратчайшему пути. Хотя вердикт от этого не изменится)

      → Ответить
»
12 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

J: к сожалению, максимально удаленная от вершины точка не обязательно является вершиной. gchebanov предложил, реализовал и зааксептил следующее решение:

ясно, что расстояние от вершины до какой-то точки на "противоположной" грани параллелепипеда можно посчитать, исходя из трех разверток (два раза через одно ребро и, если точка достаточно близко к противоположной вершине, один раз через два ребра), за О(1). Так давайте решим задачу с помощью двух тернарных поисков (по осям x и y) на трех противоположных гранях.

Буду очень благодарен, если кто-то расскажет, должно ли это заходить, и почему)))

→ Ответить
  • »
    »
    12 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    ИМХО, при сдвиге конечной точки по ребру мин расстояние не может увеличиться, поскольку ни одно из расстояний d1, d2, d3, предложенных Harhro94, не увеличится. Ведь каждый из этих трёх путей может быть реализован двумя способами (3 грани у нас как начальный выбор, куда идти, от каждой ещё 2 ведут к искомой точке; 3*2/3 пути=2). И если порисовать, то видно, что хотя бы у одного из этих двух способов длина больше никак стать не может, для каждого "d".

    → Ответить
  • »
    »
    12 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

    Моё мировоззрение внезапно изменилось, когда я сдвинул точку по двум координатам и такого же результата не получил.

    → Ответить