Примерно через 25 минут начинается очередной SRM. До закрытия регистрации еще 10 минут.
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | jiangly | 3898 |
| 2 | tourist | 3840 |
| 3 | orzdevinwang | 3706 |
| 4 | ksun48 | 3691 |
| 5 | jqdai0815 | 3682 |
| 6 | ecnerwala | 3525 |
| 7 | gamegame | 3477 |
| 8 | Benq | 3468 |
| 9 | Ormlis | 3381 |
| 10 | maroonrk | 3379 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 165 |
| 3 | Dominater069 | 161 |
| 4 | Um_nik | 160 |
| 5 | atcoder_official | 159 |
| 6 | djm03178 | 157 |
| 7 | adamant | 153 |
| 8 | luogu_official | 150 |
| 9 | awoo | 149 |
| 10 | TheScrasse | 146 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2025 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 31.01.2025 11:41:08 (k3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











OK :(
как решается div1 500?
Возьмём множество из всех атомов. Найдём отсутствующее ребро, у которого оба атома в множестве. Понятно, один из них надо исключить, переберём какой, уходим в рекурсию. Если всё ок — берём сумму атомов во множестве и улучшаем ответ.
Так как мы можем исключить всего 16 атомов (50/3) , то и ветвлений всего 2^16.
Должен работать такой перебор: Берем все вершины и находим наименьшую пару (i, j) что между i и j нет ребра. Рекурсивно перебираем, выкинув либо i либо j. Т.к. глубина не больше n/3, получаем O(2^(n/3))
Еще можно или даже
или даже 
Будем решать задачу на дополнении. Тогда это найти вершинное покрытие размера не более чем. Тогда вершину степени <= 1 мы точно не возьмем. А иначе можно либо взять, либо не взять. Тогда удаляется либо вершина либо два соседа. Получаем рекурентность на Фибоначчи.
А можно отдельно разобрать случай всех циклов. Тогда будет выкидываться хотя бы три вершины в одном из случаев.
Да, точно. Я примерно так решал http://acm.timus.ru/problem.aspx?space=1&num=1695
А там то оно что даст? 1.61n?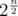 . Просто добавить запоминание к перебору.
. Просто добавить запоминание к перебору.
Есть же халявный
1.61^n с мемоизацией работает намного быстрее чем 2^(n/2), и видимо это единственный способ сдать эту задачу на Java :)
Посоны, посоны, алгоритм с Википедии заходит? Говорят, работает за O(3^(n/3)), у меня два дефенда и единственная выжившая 500-ка в комнате.
UPD. Не заходит :(
где n — количество максклик(которые нельзя увеличить)
автор ниже прав, я не умею читать :(
где n — количество вершин в графе
У меня алгоритм Брона-Кербоша зашел в практике после отсечения (если кандидатов не хватит на достаточно большую клику), максимум 684 мс. Подскажите, это дырка в тестах или правда этого отсечения достаточно? http://pastebin.com/icARB4fb
Из моего кода в 250-ке внезапно пропала строчка, которая добавляла .mp3 в конец всех названий. То есть, сначала я действительно ее не добавил, но потом добавил и отослал. У кого-нибудь что-нибудь подобное было? Пользуюсь kawigi.
compile нажимал, или только run tests?
черт, это возможно. обидно. очень странно, что оно не напоминает о том, что я отсылаю неактуальный код. спасибо.
Буду благодарен если напишете Div2-1000 :)
я так понимаю она идентична div1 500? Она обсуждаеться выше
Для начала создадим порядок в обходе всех ребер. Теперь пустим рекурсию по состоянию. В начале у нас пустое множество. Пусть на каком-то шаге у нас образовалось мн-во А, |A| = t. Найдем все ребра вершины которых не лежат в A. Если таких ребер не нашлось, то из вершин не лежащих в А возьмем k-t вершин с максимальным весом добавим и обновим ответ. Иначе возьмем первое ребро и закинем сперва первую вершину, а затем вторую. В итоге у нас получается О(n * n * 2^k).
Быстро однако ответил :)
Кто-нибудь умеет доказывать такое решение 500ки: 20К раз пошафлим вершины и жадно наберем клику?
Казалось бы, падает на полном графе, в котором удалено штук десять ребер.