ftiasch's blog

[help] PA 2011 Problem — The Shortest Period
By ftiasch, 12 years ago, In English

http://main.edu.pl/en/archive/pa/2011/naj

problem: find length of shortest period after removing exactly one character from the given string.

the period of string s is the shortest string t which s is a prefix of tk for sufficiently large k, where tk denotes t + t + ... + t (k times).

i have already got some idea of the algorithm, is there any algorithm running in O(N) time?

thanks in advance.

  • Vote: I like it
  • +17
  • Vote: I do not like it

»
12 years ago, # |
  Vote: I like it -33 Vote: I do not like it

You have to use segment tree and BS Tree their subtrees' roots being hashed (using perfect hashing !) and finally BS on answers while also balancing the red-black tree, and maintaining the fact that the sum is even if the number of subtrees' nodes are 2^p-1, where p is any prime number.

Also take into account that 64MB stack is not enough to recursively solve the problem. You gotta use an iterative method.

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    i saw you use segment tree in your solution, is your the running time be O(N log N)?

    → Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +23 Vote: I do not like it

    Guys, this man(i mean Dixtosa ) always write the same text to all blogs that ask for help.

    he wrote the same thing in this blog

    and do you know why he do so? he do so to get negative votes and make his Contribution the least one in codeforces so give him positive vote :) .

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
      ← Rev. 4   Vote: I like it -36 Vote: I do not like it

      ur awesome :d

      it must have taken you long to infer that, doesn't it? :D

      Lastly, don't fucking ever try to decipher me again plz :D

      → Reply
      • »
        »
        »
        »
        12 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        no it didn't take me long to infer that :)

        By the way, I gave you positive votes to all your comments :)

        → Reply
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can you explain your O(NLogN) idea? May be we can improve it to O(n) together.

→ Reply
  • »
    »
    12 years ago, # ^ |
    ← Rev. 4   Vote: I like it 0 Vote: I do not like it

    the running time is due to .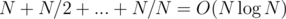

    Do enumeration on the period length L. Assume that we DO NOT remove any of the first L characters, we can check the answer in O(N / L) time.

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      The length of the period is always a divisor of N - 1 so the actual running time is O(σ (N - 1)) = O(N) I don't know how to read problem statements

      → Reply
      • »
        »
        »
        »
        12 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        In this task the length of the period can be not a divisor of N — 1.

        → Reply
    • »
      »
      »
      12 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      How is the time complexity of O(N / L) achieved?

      → Reply
      • »
        »
        »
        »
        12 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        my approach need some data structure to test the equality of two substrings. (hash, suffix array etc).

        since the period is known by enumeration, we can extend the period from both directions, so that the only character left is the one should be removed.

        → Reply
        • »
          »
          »
          »
          »
          12 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          N + N/2 + N/4 + N/8 + N/16 ... N/(2^k)=N(1+1/2+1/4+1/8 ... 1/(2^k))

          but:

          1/2 + 1/4 + 1/8 + 1/16 ... 1/(2^k) is always less than 1 (whatever the value of k)

          so:

          N(1+1/2+1/4+1/8 ... 1/(2^k))=N(1+1)=2*N

          your solution is already O(N)

          → Reply
          • »
            »
            »
            »
            »
            »
            12 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            you have made some mistake i think. the summation should be n + n / 2 + n / 3 + ... + n / n instead of n + n / 2 + n / 4 + n / 8 + ... thus the running time will still be O(n log n)

            thank you at all.

            → Reply