kingofnumbers's blog

What is the best data structure for this problem
By kingofnumbers, 12 years ago, In English

Hi,

problem:

Given an array with N elements you have to execute two different types of querys:

1- add to the array an element with value X (anywhere).

2- answer how many elements which have value bigger than l and smaller than r.

constrains:

number of querys<=100,000

N<=100,000

l<=r<=N

X<=10^9

I think it can be done using self-balancing binary search tree (for example AVL tree),

but is there is a way easier than this data structure?

I need an ONLINE solution

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
12 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I'd use treap with implicit keys.

Take a look:
http://www.codeforces.com/blog/entry/3767
It is called there 'Implicit Cartesian Tree'.

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Thank you.

    I will see which is easier BST or Implicit Cartesian Tree.

    → Reply
»
12 years ago, # |
← Rev. 2   Vote: I like it +8 Vote: I do not like it

I think, if X ≤ 105, you may solve the problem using Segment Tree.

If X ≤ 109, you may use Dynamic Segment Tree.

Description of data structure:

  1. At first we have only one vertex — the root

  2. All queries are processed from up to down

  3. When we want to use vertex, and it does not exist, we create it.

Asymptotics (X ≤ M, Q — number of queries):

  1. Time = O(logM) per query

  2. Memory = O(QlogM)

→ Reply
  • »
    »
    12 years ago, # ^ |
    ← Rev. 2   Vote: I like it -16 Vote: I do not like it

    I will get TLE if the segment tree is unbalanced(when I create new nodes)

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Ok, let describe Segment Tree more precisely:

      1. root = [1..10^9]

      2. if v = [L..R] then v.left = [L..M], v.right = [M+1..R], where M = (L+R)/2

      Depth of such tree is exatcly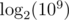

      → Reply
      • »
        »
        »
        »
        12 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        and the range that don't have any element inside it we don't create it until it have one element, right? , then we can't code the segment tree like a heap (if node index is i then its sons 2*i ,2*i+1) we have to use pointers in this case,now I got you thank you.

        → Reply
»
6 years ago, # |
  Vote: I like it -23 Vote: I do not like it

Actually, you can do it with STL. You can find it here

→ Reply