nik1996's blog

Add array elements to make them greater than or equal to k
By nik1996, 6 years ago, In English

Hi all!!

Could anybody help me solving following problem:

We are given a list of N unsorted elements, we need to find minimum number of addition operations in which the elements of the array can be added to make all the elements greater than or equal to K. We are allowed to add two elements together and make them one.e.g.

arr[]={1 10 12 9 2 3}, k=6 => Output=2

 arr[]={1 2 3 4 5 6}, k=7 => output=3

Constraints:

1<=n,k<=1e5

1<=arr[i]<=1e6

Thanks in advance!!

  • Vote: I like it
  • +2
  • Vote: I do not like it

Comments Comments (11)
| Write comment?
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I'm unsure if it's correct but I'll take a shot.

Sort the array. Ignore all elements  ≥ k. Now set two pointers at the start and end of the (new) array. While the sum is  < k, add, increase count, shift left pointer ahead. When the sum is  ≥ k, shift the right pointer back, reset the sum. Continue until the left pointer reaches the right. Check if the final sum is  ≥ k. If it is, we are done. If not, increase count by 1 because we add this to an element which is already  ≥ k. Print the answer.

I'm assuming a solution always exists, but it should be easy to extend this to include this case.

Edit: This solution is incorrect. Disregard it.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Correct me if I am wrong, what I could understand about your approach I think your algo will give output 4 for the second sample test case.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      No, it gives 3.

      (1,2,3,4,5,6) l=1 r=6 s=7 c=1

      (1,2,3,4,5,6) l=2 r=5 s=7 c=2

      (1,2,3,4,5,6) l=3 r=4 s=7 c=3

      (1,2,3,4,5,6) l=4 r=3 Termination, r>=l

      c=3.

      → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +2 Vote: I do not like it

    n = 7, k = 10

    1 1 1 3 4 5 6

    the answer should be 5 but your approach gives the answer as 6.

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Oh, well. Thanks for pointing out it's wrong.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      In the editorial also they have pointed out to add the minimum two elements but it is a wrong approach.. as it fails on the test case..

      n = 6, k = 7

      1 2 3 4 5 6

      I think that we fix the max element and increase the left index as Newtech66 pointed out but when the left index reaches rightindex-1 then clearly we are adding all the elements in the range leftindex — rightindex so it's better to greedily add the minimum elements because that might lead to a better answer.

      I think the problem basically reduces to the problem of dividing the array into maximum subsets s.t. the total sum of the subset >= k.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 2   Vote: I like it +23 Vote: I do not like it

        Yes, you are right, the problem is equivalent to partition set in the largest possible number of subsets such that sum each of them  ≥ k.

        This is NP-hard problem. If we can solve this problem in polynomial time I can solve partition problem: assume that sum of all elements is even (otherwise, there is no solution for partition problem). Let's use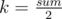 , in this case if answer equal n - 2, than partition problem can be solved, no — otherwise.

        → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        How about a recursive approach?

        Sort the array in increasing order. Ignore elements already  ≥ k.

        Let f(l, r) be the answer if we consider [l, r]. We seek f(1, n). Now, we will fix the rth element (it is the largest). Now we have two choices: we can add minimum elements from [l, x1] or add maximum elements from [x2, r - 1], where x1 and x2 are the first indices such that sum of that  +  a[r] ≥ k.

        We have: f(l, r) = min(f(x1 + 1, r - 1) + x1 - l + 1, f(l, x2 - 1) + r - x2)

        Our base case(s): If sum of the subsegment [l, r] is  < k, then f(l, r) = r - l + 1. If it is  = k, then f(l, r) = r - l.

        We can compute the required subsegment sums and x1 / x2 quickly using prefix sums/binary search.

        Again, I don't know if this is correct, and I apologise if it turns out to be wrong again.

        → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can you provide a link to the problem?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I think it's unsolvable for this constraints.

→ Reply