→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 152 |
| 6 | djm03178 | 152 |
| 6 | adamant | 152 |
| 9 | luogu_official | 149 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/21/2025 15:10:16 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Thanks for fast editorial
in div2 E , i understand spanning tree , but what you mean by dfs spanning tree , what dfs means here ?
It's the spanning tree you run through when you do a Depth First Search (DFS) on your graph (the root is the vertex you start with, etc).
gprano , but in a graph there can be multiple spanning trees , does dfs always gives us the spanning tree with largest depth ?
You won't necessarily get the spanning tree with largest depth, but the argument works for any tree you'll get that way. (it's possible that sometimes both CYCLES and PATH solutions exist but the argument guarantees that if your dfs tree has depth < n/k then the CYCLE solution works)
I really don't understand why a leaf has at least 2 back edges (edges which connected with one of ancestors). I mean why they are sure to be connected with ancestors. It's possible that they are in other brunches, right?
Sorry for interrupting.
Don't be sorry :-)
If the graph is undirected, the edges of a leaf in the DFS tree can only be ancestors : - if an edge were to a previously visited branch, because edges are bidirectionnal then the DFS would have visited our leaf in that previous branch too. - if an edge is to a not-yet-visited branch, then the DFS would visit it from our leaf (which wouldn't be a leaf anymore).
Well simply ; its because the degree of each vertex is atleast 3 ( described in the problem statement )
And a node when discovered in the dfs tree would be discovered by one of the edges. Now if degree is atleast 3 ; and 1 edge is wasted to discover the vertex ; where would the other 2 edges go ?
They will be connected to some ancestor ( As this node is a leaf and does not have any descendants )
And an edge from a node to ancestor — These are the back edges ( At least 2 ) !
Good editorial but I don't understand here about DIV1 D, why M<=12000? I mean is it the final number that has counted m times for every vector? My answer for the number of vectors (upper bound) is here:
m upper bound
1 39
2 469
3 2369
4 6734
5 10808
6 11598
7 7815
8 3462
9 895
10 110
11 4
Calculations seem correct, but M goes without multiplying by m, so, we can also say that M<=11598
Why at Div2 D the pairs are powers of two?
If we use power of 2: For the pair
[x, 2*x], ifa > xanda <= 2*x, I can show you thatx % amust be larger thanx * 2 % a. Becausea >= xanda <= 2*x,2*x mod a<=2*x - a<x. If we chose other number, we can hardly get this feature.in fact,
2*x mod a = 2*x - a < xI'm sorry, but the editorial for E is terrible. Anyone care to rewrite the editorial for E so that it is understandable also to people that do not already know the solution?
I have a solution based on FFT/NTT, but it is obviously too slow.
In particular:
No, it isn't clear. Why and how? How does the transformation matrix look like and how do you compute it fast enough? How do you use it afterwards?
What is x and how do I incorporate it into the transform?
If it can be easily shown, please show it.
How does it help to get rid of these? Also, you probably mean larger or equal to x4, right?
You just said that you eliminate monomes larger than x4. What happens to x1 through x3. Do they disappear? Why?
I apologize that the editorial was not well-written.
Thanks for the reply and clarification! I still don't understand it, but I not understand it less than before. I mean I understand the solution, but I don't understand how I should come up with it :)
In Solution 1, you use a ring modulo x5 + 1 instead of x10 - 1, presumably just to make the solution 4 times faster. Failing to notice that, along with the fact that - x4 was the inverse of x, was the main source of confusion. Also, the function smfft doesn't do FFT, but "only" DFT :)
Yeah, sorry for that, I didn't think I will publish author solution.
To come up with this idea, you might think: "Everything we need is a ring with 10-th root of one. We know one similar ring, complex numbers (i is the 4-th root of one). So let's just make our own ring, where x is the 10-th root. Then each number in this ring has a form of a_0*x^0+a_1*x_1+...+a_9*x^9". It is actually polynomial ring, but it doesn't matter. Then you somehow (I did it after writing the solution) realise that you get the answer quite not as you was expecting and you should eliminate large powers of x (for example x^7=-x^2). You come up with identity x^4-x^3+x^2-x^1+x^0=0 and actually solve the problem.
(The followings are mostly equivalent to scanhex's explanation in some sense. I just want to share how I came up with the solution. Some details, such as why DFT is used, how to divide 10 in the final step, are skipped since they are exactly the same as scanhex's explanation.)
I used the ring modulo x5 - 1. It is more natural to me. Actually, no polynomial rings appeared in my mind before I attempted to proof my solution after getting AC.
According to Wikipedia, we need a principal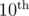 root of unity in
root of unity in 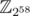 which has the exact same role with
which has the exact same role with 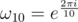 in
in  . We can easily see that - 1 is a principal
. We can easily see that - 1 is a principal 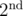 root of unity. In order to convert this root from order 2 to order 10, I extended the ring to include ω5 and thus - ω5 becomes a valid candidate. Then the ring is now extended to
root of unity. In order to convert this root from order 2 to order 10, I extended the ring to include ω5 and thus - ω5 becomes a valid candidate. Then the ring is now extended to 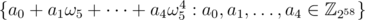 to preserve the closure of addition and multiplication. For implementation, we only need to store those a0, a1, ..., a4. In fact, 1 + ω5 + ... + ω54 = 0 (which is also required by the definition of principal root of unity). It is sufficient to store 4 of those coefficients but this increases the complexity of the DFT so I simply stored all of the 5 coefficients.
to preserve the closure of addition and multiplication. For implementation, we only need to store those a0, a1, ..., a4. In fact, 1 + ω5 + ... + ω54 = 0 (which is also required by the definition of principal root of unity). It is sufficient to store 4 of those coefficients but this increases the complexity of the DFT so I simply stored all of the 5 coefficients.
Originally, I thought the final answer is a0 in each corresponding entry after the inverse DFT, which is incorrect. In the debugging process, I found that a1 = a2 = a3 = a4 after the inverse DFT. Then I used a0 - a1 as the final answer and got AC.
The last step is correct since 1 + ω5 + ... + ω54 = 0 implies a0 + a1ω5 + ... + a4ω54 = (a0 - a1) + (a2 - a1)ω52 + (a3 - a1)ω53 + (a4 - a1)ω54. ω5 is a root of the polynomial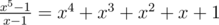 , which is irreducible over
, which is irreducible over 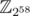 . The degree of the polynomial is 4 so the above representation with 4 coefficients is unique. Then
. The degree of the polynomial is 4 so the above representation with 4 coefficients is unique. Then 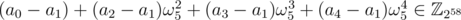 implies a2 - a1 = a3 - a1 = a4 - a1 = 0.
implies a2 - a1 = a3 - a1 = a4 - a1 = 0.
As a side note, the first idea in my mind is changing the input numbers to base 19 without changing the digits, i.e.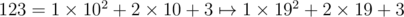 . Then we can use 1D FFT with fast exponentiation and handle the modular operation on each digit ourselves between each FFT. However, the constant factor, 1.95 is too large and the modular base 258 is not friendly.
. Then we can use 1D FFT with fast exponentiation and handle the modular operation on each digit ourselves between each FFT. However, the constant factor, 1.95 is too large and the modular base 258 is not friendly.
Thanks for adding your view!
I had the exact same idea with base 19, but not only you get the 1.95 factor for the base, you also get two factors (one for NTT and second for binary exponentiation). And on top of that you need CRT with four moduli.
factors (one for NTT and second for binary exponentiation). And on top of that you need CRT with four moduli.
I feel that all the explanations about killing x5 in the last step are mysterious and vague. So I am trying to describe my own.
The (extended) ring we actually used is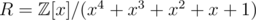 . It's clear that
. It's clear that  is the 10-th primitive root. As R is a subring of
is the 10-th primitive root. As R is a subring of 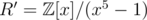 , we can do the intermediate computation in R' to save a time factor of 5.
, we can do the intermediate computation in R' to save a time factor of 5.
My biggest confusion is why the ring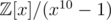 does not work. It turns out that to be used in the DFT as the primitive root,
does not work. It turns out that to be used in the DFT as the primitive root, 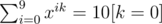 should hold along with x10 = 1.
should hold along with x10 = 1.
Please explain the approach of Game with string
Thank you
Can you finish the proof? I can get the point about irreducible, but even in that case there's still $$$2^{32} \times 2^{32} = 0$$$.
Oh, I think I can answer your question. Forget about modulo for a moment and just think that we store real values. The solution will work, except precision issues as numbers will be large. Now, let's just calculate everything modulo 2^64 instead. We can always take any algorithm and do every operation modulo 2^64, result will remain correct (as long as we don't divide by zero).
can someone help me with my solution of problem c , i am getting "wrong output format Unexpected end of file — int32 expected" on test case 14 , here is the solution to my link https://codeforces.me/contest/1104/submission/48794438
See, this is the same approach I applied which works for small length strings. Basically , you cannot guarantee of a solution using this approach and this is the reason for Wrong Answer. In your matrix after few insertions there will be a state which cannot accommodate horizontal tile.
1 T F T F T T T F F T F T F T F T
This will be the condition of matrix which cannot accommodate the tile.
thanks buddy for the help, by the way how you were able to conclude this bug in this approach
Length of string in 14 Test Case is 999. So just add a Constraint to your code to see if it print answer of every index and if not then print the boolean array. Remember not to print required answer in case if length of string is 999 Cheers :P
Few doubts in problem DIV2 E — 1) Obviously, we have three cycles here: path from x to v with corresponding back edge, the same cycle from y to v. Why it will be always the same cycle from y to v and not a different cycle? 2) Lengths of these cycles are d(v,x)+1, d(v,y)+1 and d(x,y)+2, where d(a,b) — distance between vertices a and b. It's clear that one of these numbers is not divisible by three. Why one of them will not be divisible by 3? Still I am having these doubts, anyone please help.
Suppose d(v,x) + 1 and d(v,y) + 1 are divisible by 3 and d(v,y) > d(v,x). d(x,y) = d(v,y) — d(v,x) = (d(v,y) + 1) — (d(v,x) + 1) is divisible by 3 too. Hence, d(x,y) + 2 is not divisible by 3.
"Why it will be always the same cycle from y to v and not a different cycle". It differs, but has the same form (path with the back edge).
I am not sure how you got this formula — d(x,y) = d(v,y) — d(v,x) Please tell if I am making some basic mistake.
If y and x both are ancestors of some vertex 'v' ; then y,x and v all form a chain. Draw this on a paper ( In order y , x , v ( As he says dis(y,v) > dis(x,v) ) ; and you will see how !
Why we have taken power of 2 in problem D (game with modulo) ,I mean how that would click to someone ,Is there any mathematical reasoning behind it? Please help me ...
It seems that binary search could be useful in this problem.Lets assume that x=a and y=2a and the number must lie between x+1-y.If that's the case then number can easily be found using bin search.So we have to find out such x,y.That's why we took power of 2.First we checked 1 and 2.If 1 or 2 is not the ans then the answer is elsewhere .U know we are doing binary search.So why not use power of 2?
In problem D, O(M⋅2^m⋅m+m^2⋅4^m) is accepted,but how can we solve it in O(M⋅2^m⋅m+m^2⋅3^m) according to the editorial? Is it a typo or my mistake?
No, it's not. Maybe you have small mistake in complexity estimate, most of solutions have a component with iterating over all submask for an each particular mask which works in O(m2·3m). For example: Code
Can someone explain the approach of B. Game with string?
With reference to the editorial for problem B:
It can be shown that the answer does not depend on the order of deletions.Can this fact be elaborated on?
I tried a few cases but I'm unable to build an intuition for this. For ex., consider the string
abcbbccbb. There are several places that you can start performing operations from, but no matter where you start, you will always end up with only3operations. I can't manage to prove this though. Any help would be very appreciated.