Hazyknight's blog

A brief tutorial to problem G of Hello 2019.
By Hazyknight, history, 6 years ago, In English

The first step is how to deal with (f(x))k.Here we can use Stirling Number of the second kind. Let's define S(i, j) the number of ways to put i different elements into j sets and there are no empty set.Note that the all j sets are the same.For example S(3, 2) = 3.The three ways are {{1}, {2, 3}}, {{1, 2}, {3}}, {{1, 3}, {2}}.So we have:

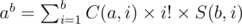
How to proof it?ab is the number of ways to put b different elements into a different sets and empty sets are allowed.The other side of the equation means we select i sets from a sets and arrange them in i! different orders and put b different elements in it. So the fomula in the statement becomes:

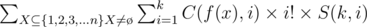
Which equals to:

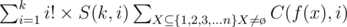
For 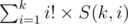we can use the following O(k2) DP to calculate all S(k, i).

S(i, 1) = 1
S(i, j) = S(i - 1, j - 1) + j × S(i - 1, j)

Which means we consider the ith element.It can form a set by its own.Or you can insert it into one of those j sets.

For 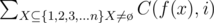we use tree DP. Let's define gij the number of sets X plus the number of some tricky situation(I'll show you what it is later) when we select j edges in the subtree of node i.In addition,there should exist a node 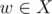for every selected edge (u, v)(depthu < depthv) that w is in the subtree of v.The initial value is:

gi0 = 2

Means we can choose node i or not. When we add an child ch of i into our DP states we go through every possible l and we select l edges in the subtree of ch or we select l - 1 edges in the subtree of ch and select edge (i, ch).So we have:

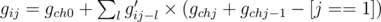
Where g' is the previous state without add informations of ch.Note that in order to hold "there should exist a node 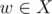for every selected edge (u, v)(depthu < depthv) that w is in the subtree of v" we have to minus 1 invalid state which is "select edge (u, v) but select no node in the subtree of ch". And for answer,we have to know what are those tricky situation.For example,we only select nodes from one subtree of i and some of the edges cannot be selected according to the defination of f because none of their ancestors is selected.So we have to go through all the children of i and minus them.Let's define hij be the number of sets X when we select j edges in the subtree of node i.So we have:

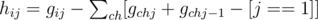
And now we finally have:

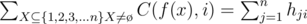
The total complexity is O(nk + k2). Why is the complexity O(nk + k2)?Calculating Stirling numbers is O(k2).And for DP on tree,when we merge two subtrees A and B with size sizeA and sizeB,the complexity is O(min(sizeA, k), min(sizeB, k)) which also means to merge the right min(sizea, k) edges from A and the left min(sizeb, k) edges from B.So if we put all edges in a line and two edges all be merged only if their distance  < 2k.So the complexity of DP is O(nk).

My code:https://codeforces.me/contest/1097/submission/48058882

  • Vote: I like it
  • +248
  • Vote: I do not like it

»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Cool! I've been waiting for the editorial for a long lime!

Thank you very much!

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

"Or you can insert is into one of those j sets." -> "Or you can insert it into one of those j sets."

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why is the complexity O(nk)? I can show that its O(n × min(n, k2)), and I was convinced that it will be O(nk), but I don't see any actual reason for that, nor never heard of it.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    When we merge 2 subtrees with size a and b, it costs time complexity of Θ(min(a, k)·min(b, k)), we can consider these vertices laying on a line, then Θ(min(a, k)·min(b, k)) comes from the right min(a, k) vertices of subtree 1 matches with the left min(b, k) vertices of subtree 2, a pair of vertex will cost Θ(1) time if their distance on the line  ≤ 2k. So the total complexity is Θ(nk).

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I add some proof of complexity in the blog.See if you understand why.

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    A pair (u, v) has the contribution only if |pos[v] — pos[u]| <= 2k where pos[v] is the index of node v in the DFS order. Thus, it's O(nk).

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

One thing I may add is S(n, k)·k! = (S(n - 1, k - 1)·(k - 1)! + S(n - 1, k)·k!)·k. So we don't need seperated formulas for the Stirling numbers and the factorials.

→ Reply
»
6 years ago, # |
  Vote: I like it +48 Vote: I do not like it

I had some blog on the proof that the complexity is O(nk)

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I think the tricky situation is that the chosen set X is in subtree of node i's one child, but i is not chosen. In this case we should not add to answer twice. Add using a^b by Stirling Number is really beautiful. Thanks a lot for your editorial.

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Thanks for the explanation. I'm still confused about the final equation: why is it a sum over hji, rather than just h0i (the numbers of sets X when we select i edges in the whole tree)?

I'm confused about the previous equation too, but I think that'll become clearer once I understand exactly what h is.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think I have it: hij is the number of sets X with j selected edges in the subtree of i for which i is the LCA of X. So in the final formula you need to sum over all possible LCAs, and in the second-last formula, you're subtracting the cases where all selected vertices come from one of the children.

    → Reply