viren0's blog

Nim Game
By viren0, 6 years ago, In English

ff

ff

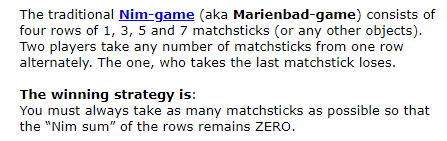
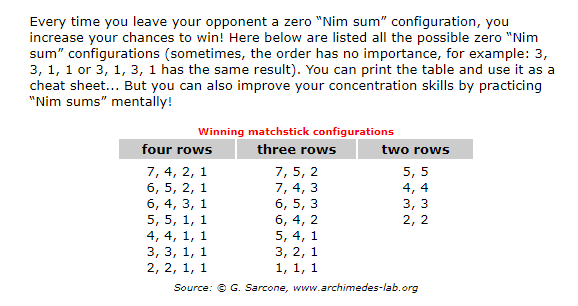
I don't understand for 1, 1, 1 XOR is not 0 but it is a winning position. I know how Nim game where last mover wins works but I am having hard time to understand this version.

Also, how to know which position is a winning position like in other version we see that when piles are empty XOR is 0 hence, XOR 0 is winning position.

Source

  • Vote: I like it
  • +7
  • Vote: I do not like it

Comments Comments (4)
| Write comment?
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

1,1,1 is winning because the xor is not 0. Any position where the xor is 0 is losing all other positions are winning. If you are in a position where the xor is not zero the winning strategy is to remove some matches to make the xor 0 so your opponent is in a losing position.

They really shouldn't have used the word "remains" in the winning strategy description.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    But if you see 2, 2 is also a winning position and I don't remember there are exceptions to Nim strategy. I guess if played optimally 1, 1, 1 will never be a position.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      My bad. The notes I have describe a nim game where the person to take the last stick wins. In the game you describe the person who takes the last stick loses. My notes call this the misère game and the strategies are opposite. So it looks right you're right about the 1,1,1 being losing.

      → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +11 Vote: I do not like it

This is a different Variant of NIM called the Misere Nim, where the last person picking loses.

You can Google the Term 'Misere Nim' to get the proof for the result.

Misère Nim is exactly like the standard Nim game, except for one critical difference. If the size of every pile is 1, then we need to treat it as a special case where we count the number of piles. If the count is even, then the first player will win; if the count is odd, then the first player will lose.

If the size of every pile is not 1, then you can use XOR sum to determine who will win the game.

→ Reply