Olá a todos!

The first winter weekend of the year would be tough for students who arrive to St. Petersburg, Barnaul, Almaty and Tbilisi. On the 1-2 of December ITMO University, Altai State Technical University, European University and Kazakh-British Technical University will host the final contest of Northern Eurasia. Participants are going to face a serious competition – they will fight for the right to represent their university on the finals of the ICPC 2019 in April in Portugal.
At the ITMO University stage we also expect 131 teams, including the Champions and Vice-Champions (but, worth mentioning, NEERC Champions) from last year ICPC'18.
Stay tuned for the latest news and monitors from the competition! These guys will go to the Porto to represent our Northern Eurasian region! Participants of our region have been taken the Final ICPC Cup for the last seven years. Will they continue their series of victories? Will see!
UPD: To the finals ICPC 2019 were qualified 15 teams:
- Moscow SU 3 (Makeev, Reznikov, Ipatov)
- Moscow IPT 6 (Sergunin, Belykh, Stepanov)
- International IT U 1 (Satylkhanov, Baimukanov, Kuanyshbay)
- SPb ITMO University 2 (Poduremennykh, Naumov, Korobkov)
- SPb br of NRU HSE 1 (Ermilov, Fedorov, Labutin)
- U of Latvia 2 (Klevickis, Pretkalnins, Pakalns)
- SPb SU 5 (Grebennikov, Fadeeva, Zavarin)
- Belarusian SU 1 (Lukyanov, Rak, Kim)
- NRU HS of Economics 1 (Sakhabiev, Nikolenko, Gribov)
- Kazakh-British TU 1 (Amanov, Aman, Zhussupov)
- Saratov SU 1 (Androsov, Glazov, Dalabaev)
- Belarusian SUIR 1 (Mosko, Razhkou, Shilyaev)
- Tbilisi IBSU 1 (Ksovreli, Narushvili, Svanidze)
- Northern FU (Dyachkov, Guriev, Asyutchenko)
- Ural FU 6 (Permyakov, Zuev, Mullabaev)
Follow the official competition hashtag #NEERC and join a live video, organized by ICPCLive and, in person, Aksenov239.
We are pleased to notice that this year at the NEERC will be special! We host some unique guests from the Committee of the ICPC organization – the Executive Director of the ICPC, Dr. Bill Poucher and Deputy Executive Director of the ICPC, Dr. Jeff Donahue. We will passionate to hear some inspiring words for our teams from Bill! And, of course, don’t miss the interviews with our special guests live!
If you want to visit the championship as a guest – please fill out the form.
If you do not participate in the semifinals, you can try to solve problems from 23rd NEERC challenge in the mirror. It will start in a few minutes after the main round on December 2nd. The tasks will be provided in English only. The mirror is an unrated contest.
We have compiled a table of participating teams with the total Codeforces rating >= 7000. Who is your favorite thou?
| Team | Participant 1 | Participant 2 | Participant 3 | Rating |
| Moscow SU: Red Panda | Ipatov (LHiC) | Reznikov (vintage_Vlad_Makeev) | Makeev (V--o_o--V) | 7788 |
| Moscow IPT: Shock Content | Stepanov(irkstepanov) | Sergunin(AndreySergunin) | Belykh(WHITE2302) | 7689 |
| Moscow IPT: Good Game | Golovanov(Golovanov399) | Uvarov(-imc-) | Machula(mHuman) | 7671 |
| SPb SU 1 | Gorbachev(peltorator) | Ivanov(orz) | Safonov(isaf27) | 7638 |
| SPb ITMO University 1 | Sayutin(cdkrot) | Kirillov(craborac) | Drozdova(demon1999) | 7604 |
| Moscow IPT: Racoons | Grigoryev(DmitryGrigorev) | Tretyakov(ShadowLight) | Shpakovskij(Denisson) | 7440 |
| SPb SU 2 | Milshin(Morokei) | Filippov(step_by_step) | Fedorov(DaniilF) | 7367 |
| SPb ITMO University 2 | Korobkov(romanasa) | Poduremennykh(PoDuReM) | Naumov(josdas) | 7360 |
| Moscow SU: NoNames | Kalendarov(Andreikkaa) | Koshelev(SendThemToHell) | Chunaev(ch_egor) | 7243 |
| NRU HSE: IOI is not ICM, said MS | Nikolenko(qoo2p5) | Gribov(grphil) | Sakhabiev(super_azbuka) | 7052 |
| Saratov SU #2 | Androsov(BledDest) | Dalabaev(adedalic) | Glazov(Roms) | 7000 |
Вoa sorte! Siga-nos:

















Why does vintage_Vlad_Makeev make his rating lower on purpose?
for fun
I guess he wants to grow his account from green to red again. Just for fun.
Why does this comment have so many minuses?
Aggresive nerds.
So that he will not get PMs of the form: how to become red/ICPC champ in one year?
Can Some one tell How M Minegraphed Can be tested!
How does system check a submission is right?
Why doesn't SpyCheese join participate in this contest ?
hăăpp-ciu!
What is formula of counting team rating?
a + b + c
i mean on mirror contest team ratings, you noob
click. Also this blog is about NEERC, so you should have clarified that you need codeforces team ratings.
Is iT rAted?
Has there ever been a rated team contest?
of course yes!
like this one VK Cup 2018 - Round 1 XD
I've always wondered that if they have a particular system for rating teams, why almost every team contests are unrated??
khar_khar You should give our Chinese a reason.
No, he only discriminates against chinies.
Excuse me.What's the difference between these?
The difference is knowing how to write.
Oh, My friend just have a talk with this guy. His English,Emm.. not really good. But this team's name, just tell us his racism.
Was this part of vintage_Vlad_Makeev's master plan?
Isn't it funny — a team of 2xLGM and green?
It is funny, but is it worth it?
I couldn't register as a team in this contest, though I am the founder of the team. What should I do?
same here. I cant register too. The team dropdown list is empty when I wanted to register as team.
I meet the same problem. Have you got any solution? (I have been successfully registered, thanks!)
Fixed
Thanks.
How many problems in the contest?
The page crashes when you try to view friends' submissions.
UPD: Seems to be fixed.
Thanks for giving us the opportunity to take participate in the mirror contest.
Really great problems.
We really enjoy this contest.
how to solve c?
On a tree this problem is solvable with centroid decomposition. We find centroid, print it and if it's not the chosen vertex, we go in one of its subtrees.
For cactus, let's build tree of vertices and cycles: for each cycle, delete all it's edges, create a new vertex and connect it with all vertices in the cycle. On this tree, let's find a weighted centroid: all real vertices have weight 1 and all added vertices have weight 0. If this centroid is a real vertex, then we guess it, and go to one of its subcactuses. If it's a cycle, then if we ask some vertex v on this cycle, we will know that the chosen vertex is either in subcactus of some vertex to the left of v, some vertex to the right of v or in subcactus of v itself. So each v splits graph in three parts. We know that subcactus of v is always not larger than n / 2 because we chose centroid. We need to choose such v so that other 2 parts are also not greater than n / 2. It turns out that it's always possible. Let's choose some v, if the part to the right of v is too big, then the part to the left and subcactus of v together are not greater than n / 2, so if we shift v to the right, then the part to the left of v is still small. If we do this, we will stop eventually. There is also a case when the cycle length is even, then parts to the left and to the right of v are intersecting, but the proof still works with some minor fixes.
Now that we have this proof, we can actually do a brute-force search: for each vertex in the current subtree, compute the worst-case number of vertices remaining in the tree after we ask the question. We can therefore come up with an "optimal" query in O(n2) time.
In order to get accepted, I needed to do some minor optimizations (memoize the optimal queries for each subtree). This gives us an O(n3) solution which fits comfortably in TL.
Edit: we just realized that the memoization brings the runtime to O(n2). :)
No need for any optimization: My submission during contest
You can always choose a vertex which has smallest sum of distances to (all vertices which could be answer right now). After that the set of vertices which could be the answer becomes at least two times smaller.
Also this works for all graphs, not only for cactus.
Can you give proof why the set becomes 2 times smaller(for general graphs) ?
Let's say we asked vertex v, Chloe responded with w and set didn't become 2 times smaller. Vertex u stay in the set iff dist(v, u) = dist(w, u) + 1.
If this condition is true for more than half of candidates than we should choose vertex w instead of v because it has smaller sum of distances to set: (at least half of distances is smaller by one) + (less than half of distances is bigger by at most one). Contradiction.
Wow! That's magic! If it works for general graphs why haven't you posed a question like that instead of just for cacti? For cacti it is much more intuitive that we can do this, not surprising at all and easier to come up with, while for general graphs it is very surprising and more fun to solve.
Probably because problems on cactus is a "feature" of NEERC?
There are several reasons for doing that:
There will be a day when the first argument will be thrown away, or at least won't be the first in the list. The other arguments make sense though.
What is reason for WA on test 10 in A?
i had wa 10 because for some test, we answered
2:325:a b:25 c:25 d:25 15:ewhere a,b,c,d,e — some numbers (i can't remember now)
why the codes are not seen after final standing.
What kind of matrix do I need to compute determinant of in order to solve B :p?
It's a well known maximum cost general graph perfect matching problem in China.
In Moldova we can say the same thing about sorting.
peltorator, take notes
How come every problem is well known in China? And yet Chinese teams always lose to Northern Eurasians in ICPC finals.
Most strong competitors in China are high school students, and they spend less time in the algorithm competition in the university.
And I want to say the problemset this year is not original enough. Someone also sent the problem I with constraint n = 2000 to me eight months ago.
How exactly should we use it? We thought about the reduction during the contest but couldn't come up with one.
Let G = (V, E),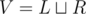 . We will perfrom two reductions.
. We will perfrom two reductions.
First, let us reduce the problem to "minimum weight matching in general graph that covers all vertices from ". In order to do so, let us replace each vertex
". In order to do so, let us replace each vertex 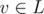 with two copies v - and v + , connect each of the copies with the original neighbors of v (that belong to the R) with zero-cost edge and connect v - and v + with an edge of cost 1.
with two copies v - and v + , connect each of the copies with the original neighbors of v (that belong to the R) with zero-cost edge and connect v - and v + with an edge of cost 1.
Now any matching that covers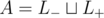 expresses some bimatching: if v - is connected with v + , then vertex v does not belong to any triple, and otherwise it belongs to a triple with the pairs of v - and v + , and each spare vertex costs 1 unit of penalty.
expresses some bimatching: if v - is connected with v + , then vertex v does not belong to any triple, and otherwise it belongs to a triple with the pairs of v - and v + , and each spare vertex costs 1 unit of penalty.
Let's now find out the minimum weight matching that covers A. In order to do so, replace G with two disjoint copies of G: G1 and G2. Now connect v1 with v2 for all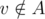 with edge of cost 0. Now any perfect matching in this graph consists of several edges between v1 and v2 that we treat as uncovered vertices in G (they are outside of A, so that is fine), and the remaining matching part in, let's say, G1 will necessarily cover all A.
with edge of cost 0. Now any perfect matching in this graph consists of several edges between v1 and v2 that we treat as uncovered vertices in G (they are outside of A, so that is fine), and the remaining matching part in, let's say, G1 will necessarily cover all A.
That is one of the most beautiful problems I ever saw on NEERC.
UPD: my solution is almost equivalent to what jqdai0815 written above (though the reduction is of linear size). I was late by 3 minutes :)
UPD2: one more observation applicable to both mine solution and the jqdai0815's above: as all edges in the graph have the costs of 0 and 1, we do not need the weighted maximum matching algorithm: simply find the maximum matching in the subgraph formed by zero cost edges (this graph is still non-bipartite, though).
Any ideas on how to solve it if we had to match each vertex on left with some k ≥ 3 vertices on right?
How to solve K?
I used a segment tree, and for each node [left, right] (with respect to times of people queuing) i held some values so that i could calculate finish time of people in this interval. Those values are: Sol (the actual answer), First (time of the first guy that queues), Free (How much can i get pushed by something from my left so that my solution won't get affected by it), and Cnt (Number of people waiting). The Cnt value i think you can get rid of it, but i used it just to make sure i calculate the correct values. Of course other solutions exists, this is what i implemented.
Can you share your code with us?
Sure. 46494475
Approach is same as for timus 2014
Couldn't that timus problem be solved with a seg tree of size 365*24*60 ? . So is that the intended approach or is there some other thing?
It could. Problem K as well might be solved with quite same segment tree of size 106.
Any other approaches? Lot of solutions only use a max segment tree.
How to solve I?
http://oeis.org/A111111
On onsite competition internet is not allowed, so we didn't use it either. So what I meant is: how to solve it without oeis or google?
My solution: dp[n][k] the number of permutations of integers from 1 to n in which the first interval starts at k. Group the interval at k into a single value then compressing values, the new permutation is interval-free or the first position an interval appears is not less than k (except case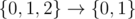 ).
).
How to solve M?
I placed strongly connected components on the same level, and made zone with "lifts" between layers, as edges between components. Possibility to climb up is useless, as it's simpler without it.
Input:
Output:
thx!
Hints on how to solve F?
You can find answer with just two fractions.
Proof?
the proof is the fact that a lot of teams got OK using just two fractions
Basically, we are trying to solve this problem.
We have a_1/d_1 + a_2/d_2 + ... a_m/d_m = (n-1)/n where d_i is the i-th divisor of N.
If we multiply everything by n, we see we have a linear diophantine equation.
a_1*(N/d_1) + a_2*(N/d_2) + ... a_m*(N/d_m) = N-1
As we know that all the values divide by N, in order for there to be a solution for N-1 on the right, the gcd of the values must be 1. As solving diophantine equations for multiple variables is too hard, we notice that if we choose a d_i = p^k, where p does not divide (N/p^k) (ie: d_i contains all of the factors of p in N), then N/d_i must be coprime with d_i. As such, we can just solve a 2 variable linear diophantine equation and get the solution.
There is a little bit of a wrinkle that you need positive solutions, but that's not too hard.
Let v is a divisor of n such that gcd(v, n/v) = 1 (if v does not exist, the answer is NO). Juse choose a1 = (n/v)^-1 * (n-1) mod v, b1 = v, a2 = (n-1-a2*(n/2))/v, b2 = n/v. You can see that a1<b1, a2<b2 and a1/b1 + a2/v2 = 1 — 1/n.
The first three teams with highest rating ranked also top 3 in the final standings!
So to me seems like a notorious coincidence
How many teams from Northern Eurasia are going to the finals?
15
Thanks.
How to solve D?
analysis
Thanks a lot!