Hello Codeforces.
RECursion, the coding community of NIT Durgapur, is organizing coding contest RECode 4.0 which will be held on 13 November at 16:00 UTC. We invite you all to participate in the contest.
The contest will be held on Hackerrank platform. The contest consists of 6 problems to be solved in 2 hours. There are exciting prizes for overall winner and college winner.
The RECode 4.0 is over, Ranklist is as follows:
- Teo Moroianu
- Jeffrey Ho
- Kerim Kocekow
- Uwi Tenpen
- Farhod Farmon
- Teimurazi Toloraia
- Saharsh Luthra
- abishek a
- Nishant Arya Kumawat
- Victor Forbes
UPD : Editorials
Auto comment: topic has been updated by rishup132 (previous revision, new revision, compare).
I am beginner. Can i participate in this contest??
Yes, you can.
Just do it!
Is it rated?
No, It is not rated contest.
What you mean by institute winners?
Institute winners for only NIT Durgapur, or institute winners for every institute?
Only for NIT Durgapur. Also, apart form that overall winners will get goodies.
Is "overall winners" equal "international winners" or you consider only Indian participants?
Yes. Overall winners include all those participating. But, goodies shall be distributed on the basis of economic feasibility.
What does winners mean here? Only rank 1?
NO, 2 overall winners + 2 NIT Durgapur winners.
Do you guys have any idea on this?
Edit: For those who wanted to read, there was a random guy who reported a question name something like "How to solve 'Watari Queries'?" before the starting of contest.
Quite good, huh?
That guy was potato_corner.
How to solve E(Apple and Ryuk)?
Let ai = 1 if there is an apple in position i, and 0 otherwise. The problem becomes, for each 0 ≤ d ≤ N - 1 calculate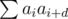
.
If we set two polynomials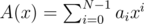
and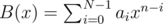 
then the coefficients of A(x)B(x) from n to 2n - 1 are exactly the desired solution. The product polynomial can be computed by FFT.
I think bitset is much easier. For ith number, answer is popcount of (a) & (a >> i).
Can you provide editorial or solution for problem D,E and F
editorials are available.
Auto comment: topic has been updated by rishup132 (previous revision, new revision, compare).
3rd question was really nice.
How to solve the last question(the gcd queries question)?
Did anyone solve Evil Group in some way other than the editorial?
Sure,there is a solution with N * log(N) * log(A[i]) for precalculation and Q * log(N) for answer queries. First let's try to find for every i biggest j which j ≤ i and gcd(j, i) = 1 and it is always monotonic. That is why we can use here two-pointer to find j for every i. Personally I used Sparse table to find gcd of given range to answer in O(log(A[i])), but you can also use segment-tree instead of it(it will take O(log(N) * log(A[i]))). After finding j for every i(let's call j as p[i]), it is easy to answer queries in offline. Just go from 1 to n and every time increase for every i the range between 1 and p[i](you can use lazy propagation to increase range or you can easily use Fenwick tree instead of it). Then for every i, just answer all queries which R = i, which answer will sum of range (L, R).