Hello, Codeforces!
We intend to share some ACM-ICPC regional contests with you! Here is one of them.
An online-mirror contest of 2018-2019 ACM-ICPC, Asia Nanjing Regional Contest will start on Saturday, November 17, 2018 at 18:00 (UTC+8). You may register for this contest 6 hours before it starts, but it is temporarily inaccessible before registration starts.
By the way, this contest will consist of 13 problems and you can solve them within 5 hours.
Wish you will learn great experience through that time!
Waaaaait!
There is another online-mirror contest, The 2018 ACM-ICPC Asia Qingdao Regional Contest (Mirror), which will be held at acm.zju.edu.cn on Saturday, November 10, 2018 at 12:00 (UTC+8), a week before the contest on Gym!
This contest is prepared by our friends from Zhejiang University and indeed a very interesting contest. If you are eager to participate, please do not hesitate to register a handle on it and take part in time!
P.S. Please do not discuss any solution before contests are finished. Thanks for your cooperation.
UPD1: Ranking that suits for Gym has been parsed from data provided by the host school (Nanjing University of Aeronautics and Astronautics). Enjoy it.
UPD2: Registration starts. You may view this page to register.
UPD3: In order to be consistent with the onsite one, the duration is extended by 10 minutes.











Bravo! Many thanks to skywalkert for sharing this contest on Codeforces and also recommending the Qingdao Regional Contest prepared by us~
I am pretty sure that these two contests are both very interesting and worth practicing since I watched the whole match on the spot. From my opinion, I am very excited to see the result of talented teams from all over the world participating in Chinese ICPC Regionals. The comparison must be very interesting.
BTW, I hope there will be more and more Chinese ACM-ICPC Regional Contests being shared on Codeforces Community. So we can practice and discuss about them afterwards~
Is it rated?
Of course not
Oops, it is coincided with an opencup round. May you change the time?
Thanks for your reminder! Would it coincide with other contests if online-mirror contest starts one day in advance? If suitable, we can shift it to an earlier date.
UPD: Starting time is advanced from Sunday to Saturday. Wish you all have known.
Can't wait to take part in the online-mirror of Asia Xuzhou Regional Contest! Should I expect it or not? Whatever, thank you, skywalkert.
Indeed, You can see it sooner or later. BTW, Asia Xuzhou Regional Contest is extremely difficult, compared to this one. :)
(:ᗤ」ㄥ)
The link is unavailable now....I just enterd the home page of codeforces when I click on it.
As it is temporarily inaccessible, please be back just 6 hours before the starting time.
Is there a tutorial available for the Quindao Regional contest? I want to know the solution for problem I and L.
L: if m > n, the answer is 0, and if m = n, it's just number of ways to make a single cycle.
if m < n, then the graph is just k = n - m paths (some may be trivial though). Let's say we fix that there are d non-trivial components (have at least 2 vertices).
Then there are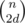 ways to choose the endpoints of the non-trivial components, and for each choice, we want to find number of ways to pair them up, which is
ways to choose the endpoints of the non-trivial components, and for each choice, we want to find number of ways to pair them up, which is 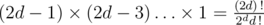 .
.
From the remaining vertices, there are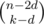 ways to choose the vertices in the trivial components.
ways to choose the vertices in the trivial components.
And finally, the remaining vertices can be freely permuted and then distributed à la balls and bins, in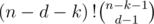 ways -- during the contest, I did this part with Exponential Generating functions; it requires more theory, but very little creativity, so it's easier for me.
ways -- during the contest, I did this part with Exponential Generating functions; it requires more theory, but very little creativity, so it's easier for me.
We also had to add an edge case for m = 0 (the answer is 1).
(edited to fix grammar)
I: There are at most O(n) segments to group. So let's sort them and make a two-pointer. What we need to do is to check whether there is a valid division. Segment tree works here, since the information of two segments can be merged easily.
I: Sort the valid 2 * N - 1 intervals by their weight. Let's enumerate the minimum and find the corresponding maximum. Consider a simpler problem: Given some intervals (Li, Ri], find whether we can cover the interval (0, N] without overlapping. It's equivalent to finding whether we can reach N from 0 by the edges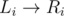 . Because the length of a interval is at most 2, we can maintain a segment tree, where the segment [L, R] stores the connectivity between [L, L + 1] * [R - 1, R]. It's easy to merge the information. Using a 2-pointer and maintaining the connectivity dynamically, we can solve the problem in
. Because the length of a interval is at most 2, we can maintain a segment tree, where the segment [L, R] stores the connectivity between [L, L + 1] * [R - 1, R]. It's easy to merge the information. Using a 2-pointer and maintaining the connectivity dynamically, we can solve the problem in  .
.
M is too difficult for me TAT. How to solve it using SAM? I know I should use manacher first, and then I can do nothing using SAM qwq.
First, count how many palindromes begin with si and let the number be fi.
Then, find the maximum length d (d ≥ 0) such that si - k = tk for each k = 1, 2, ..., d and let the length be gi.
The answer should be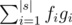 .
.
The first part can be solved using manacher algorithm as you know, and the second part is equivalent to calculate for every suffix of the reversed string rev(s) the longest common prefix (LCP) with t, which can be solved using Z algorithm.
Maybe it's an overkill to use suffix array or suffix automaton solving this problem, isn't it?
Thank you! I understand your solution. It's too difficult for SAM to solve it. I want to use SAM because ... my friend that took part in Nanjing regional contest told me: "There was a problem using SAM in this contest, I couldn't accept it because I have not learned it." So I try SAM all the time orz. And finally I think I should use prefix automation but I have not learned it LOL.
Did you know of the following solution for K (Kangaroo Puzzle)?
Just print a uniformly random button 50000 times.
This was much easier than
Iteratively finding a short sequence of moves that merges two kangaroo groups.
Why does the randomized solution work for K?
How to solve problem D — Country Meow?
I was thinking of radius of smallest sphere that can enclose all the points
I did ternary search on all 3 coordinates. Do a ternary search on x first, now for getting optimal answer for this x, do ternary search on y keeping x fixed, repeat this for z, keeping x and y fixed.
Thanks buddy. :)
Is there any proof of the monotonicity (I mean increasing first, and then decreasing.) of the answer respect to x so that we can use ternary search? Or is it just about intuition?
How to solve E — Eva and Euro coins ?
delete the k-continuous 0/1 in the 2 string and compare them
Thanks :)
Can you give a proof?
We should first show that deleting k 0s or k 1s leads to a unique result from a starting string S. This is true as if a string of k 0s is deleted in some deletion sequence from S, then in any other sequence, eventually, at least one of these 0s must be deleted, and it has the same result as deleting all k of these 0s.
Now we should show that two strings which result in the same base string can be transformed to each other. However, it's possible to move a block of k 0s or k 1s past any single character, so each string can arrive at the state 00000000 + base string by moving the blocks to the left, in order of their deletion.
I enjoyed the problemset. Thanks!
How to solve F? I had a N^3 divide-and-conquer solution for it. It has a big constant factor and gets TLE. Any better algorithm?
The first thing to explain is that the following one is not the standard solution. We just tested all the problems but didn't understand solution from the problem author. Never mind.
Let the answer matrix be F (the expected steps moving from u to v), the normalized adjacency matrix be E (the probability of one step moving from u to v), the identity matrix of size n be I and the all-one matrix of size n be J, there exists a diagonal matrix G such that F = EF + J - G. If G has been determined, what remains is to solve the equation (I - E)F = J - G.
Since the rank of (I - E) is (n - 1), we cannot directly solve the equation. But we know some additional conditions, such as Fi, i is always 0. What can we do with this condition? We may construct infinite solutions of the above equation by setting the values F1, 1, F2, 2, ..., Fn, n freely and then determining other values in the matrix. It can tell us each solution is in the form of Fi, j = FFi, j + xj where x1, x2, ..., xn are free variables and FF is any solution, so we can simply apply Gaussian elimination to reduce the first (n - 1) rows and get a specific solution FF. Then, fix the values by the condition Fi, i = 0.
Did I miss something? Emmm... The calculation of G. Actually, I don't know how to explain it easily, but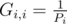 where Pi is the stationary probability (in stationary distribution of a Markov chain) that a random-walking object appears at i. You may calculate the vector P by the equations PE = P and
where Pi is the stationary probability (in stationary distribution of a Markov chain) that a random-walking object appears at i. You may calculate the vector P by the equations PE = P and 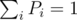 .
.
The above solution is in time complexity O(n3). However, as you've seen, there exists a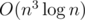 solution which applies Gaussian elimination to each (n - 1)-subsets of vertices by divide and conquer. The onsite judges thought participants who have learned this solution could soon come up with the optimized solution, so the time limit is a bit strict. facepalm.jpg
solution which applies Gaussian elimination to each (n - 1)-subsets of vertices by divide and conquer. The onsite judges thought participants who have learned this solution could soon come up with the optimized solution, so the time limit is a bit strict. facepalm.jpg
By the way, I tested the divide-and-conquer solution (without setting an epsilon) and it passed all the test cases with 1513ms, while the first one passed with 202ms. Maybe you just need some optimization on CodeForces?
The matrices are similar for all terminals. They differ by only two rows. Thus you use Sherman–Morrison formula to maintain the inverse matrix.
My solution also gets TLE during the contest.
I remember that problem setter said they used this formula in the standard solution.
Excuse me, I'm a rookie. Can you help me with problem A and B, please?
Have you ever tried to solve them independently? I'm not sure about that. But if you solved them by yourself, you might obtain some great experience, won't you?
Would someone explain the solution for H(Nanjing)?
I have a complicated idea and it runs in time complexity , which may be worse than many others.
, which may be worse than many others.
First, if there is one type of digit (at most one) that appears at least m / 2 times in the price tag of length m, the only best way is to eliminate this type of digits with other types as many as possible, and thus the cost will be calculated easily since it looks like 00... 0, 11... 1 or 22... 2.
But if no such type of digit exists, we can eliminate almost all the digits. That is, if the length of the price tag is even, we can eliminate all digits, or we have to keep one digit otherwise.
Which digit should be reserved? That digit should meet the condition that, if we remove this digit and split the price tag into two parts, each part must be able to be eliminated completely.
To find such digit, we may define ci, j as 1 if the i-th lowest digit of the first price tag is j or - 1 otherwise. For the lowest m digits, we need to find a position k such that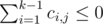 and
and 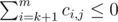 for j = 0, 1, 2. A brute-force solution runs in O(n2), so we need optimizations.
for j = 0, 1, 2. A brute-force solution runs in O(n2), so we need optimizations.
Let si, j be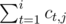 . We first pick up all possible k such that sk - 1, j ≤ 0, and then we determine if it is possible to find a digit x at position k such that k ≤ m and sm, j ≤ sk, j. Since it is a typical partial order problem in four dimensions, it can be solved by divide and conquer (offline) in time complexity
. We first pick up all possible k such that sk - 1, j ≤ 0, and then we determine if it is possible to find a digit x at position k such that k ≤ m and sm, j ≤ sk, j. Since it is a typical partial order problem in four dimensions, it can be solved by divide and conquer (offline) in time complexity 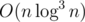 . That is, we regard each position i at (i, si, 0, si, 1, si, 2) and sort them in order of the first coordinate non-increasing, and then, during the process of divide and conquer, we sort them recursively in order of the second coordinate non-increasing, maintain the minimum x in the first divided part with the third and fourth coordinates by persistent segment tree and answer for each position in the second divided part.
. That is, we regard each position i at (i, si, 0, si, 1, si, 2) and sort them in order of the first coordinate non-increasing, and then, during the process of divide and conquer, we sort them recursively in order of the second coordinate non-increasing, maintain the minimum x in the first divided part with the third and fourth coordinates by persistent segment tree and answer for each position in the second divided part.
However, we only have to check three types of x, so we can use a segment tree (no need to be persistent) to maintain the maximum fourth coordinate in a range of the third coordinate such that this position is obtained from picked positions with digit x. The time complexity is .
.
Thank you for the clear explanation! During the contest, I reached the final part but didn't come up with the way of judging it in O(n·polylog(n)).
With your idea I think I may have found a bit easier way of solving this:
First, as you said, if the length of the price tag is odd and the numbers of each digit(i.e. 0, 1, 2) satisfy a kind of triangle inequality, then we can eliminate all of the other digits except one digit.
Actually this implies the answer must be lower than 2 under such circumstances(this is what the triangle inequality says). So what we are interested in is only whether the answer can be 0(otherwise the answer should be 1).
For each digit, let c0, c1, c2 be the number of occurrences of 0, 1, 2 in the left side of the digit respectively(because we can easily calculate the conditions for the right side, we don't care about it). Then, again from the triangle inequality, in order to keep some digit till the end, three inequalities c0 + c1 ≥ c2, c2 + c0 ≥ c1, c1 + c2 ≥ c0 must hold.
However, actually we don't have to care about the last inequality because it would be preferable if some 0s are left over. Therefore after each query we only have to judge whether there is at least one '0' digit that satisfies c0 ≥ abs(c2 - c1).
This can be checked with 2 segment trees. Both of segment trees should support Range Maximum Query with Range Update.
One of them maintains the value c0 - (c2 - c1) while the other one does c0 - (c1 - c2). The elements should be sorted in the order of c2 - c1. This order can be calculated in advance and won't change.
During each query, we can check if the maximum values of those segment trees(in the appropriate range) are non-negative. After that we can just update those segment trees with Range Update.
I just came up with this solution so I don't test this solution yet. I'll update this comment if I get AC or notice I am wrong :)
I got AC :) https://codeforces.me/gym/101981/submission/46396181
But I think most of you cannot see my submission right?
Edit: I am refering to the first contest (Nanjing).
I am trying to solve problem C. The following is the beginning of the solution but I cannot finish it:
Therefore, given that I placed at node v, and that he placed in subtree T of v, then u must be the centroid of T (because he is playing optimally).
Therefore, given that I placed first at node v, he places at centroid of subtree which maximizes (subtree size — size of biggest subtree of centroid).
Therefore, I must place at a node v such that it minimizes the maximum of (subtree size — size of biggest subtree of centroid). How do I find this node?
Thanks!
Let's assume that you chose any vertex v as first pink node and found an optimal brown node u. It can be seen that moving away from u would make one of its subtrees larger, which won't improve the solution. So we will only move closer to u.
Let's start from the centroid of the tree and call it Pink1. then find a optimal second node and call it Brown. Move Pink1 to the centroid of the subtree closer to Brown and run again. At each step we discard all the current Pink1 subtrees (except the subtree that is closer to Brown) from the potential optimal Pink1. So the number is halved each time, resulting in the complexity .
.
How to solve L?
We (testers) thought it is a notorious coincidence with Balkan OI 2017 Day 2 A. Cats. If you need a solution, just check it out.
How to solve B? IMO, this problem aims to seperate an array into k parts, such that the sum over the distance of every position to the median of its part is minimal. To solve this kind of problem in less than O(nk) time, we must assume that it satisfies the inequality ans(i) - ans(i - 1) ≤ ans(i + 1) - ans(i), and therefore we can do a binary search on the slope.
And thus, the problem is reduced to the version of no restriction on the number of parts, and thus we may let dpx denote the answer for the first x numbers, and the transferring equation is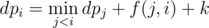 where k is the slope we have binary searched on, f(l, r) is the cost of an interval with is exactly f(l, r) = sumr - 2summid + suml - 1 where sum is the array of partial sum and
where k is the slope we have binary searched on, f(l, r) is the cost of an interval with is exactly f(l, r) = sumr - 2summid + suml - 1 where sum is the array of partial sum and 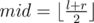 .
.
Apparently we should solve this DP in less than O(n2) time. An observation is that this DP satisfies quadruple inequality: that is, for any l ≤ a ≤ b ≤ r, f(a, b) + f(l, r) ≤ f(l, a) + f(b, r), and therefore we can use D&Q optimization to solve the DP in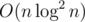 time.
time.
However, when I try to verify my idea by examing someone else's code in coach mode, I find out that most of them used Convex Hull Trick, which shaves one log factor out the complexity. Can some one please explain how this is done? Thanks in advance!
The first part of your solution is correct where you binary search on the cost associated with increasing one partition. So, now the problem reduces to solve the recurrence you mentioned optimally. As the above recurrence satisfies quadrangle inequality, you can solve it in O(n) using 1D-1D Dp optimisation. Hence the complexity would be O(n logA) where A is upper bound of cost.
How can we solve the above recurrence in O(n)?. Normally to achieve this complexity, we should notice that the equation has a form of a line on the plane and apply Convex Hull Trick. But how can this equation be rewritten in that form? Or is there anyway we can solve it in O(n) without the Convex Hull Trick, just using the property of quadrangle inequality?
The above equation can be solved without the convex hull trick in O(n). We just need to use the property of quadrangle inequality. You can look for 1D-1D Dp optimisation. It solves the above recurrence in O(n). For more details, you can refer to my code.
Thanks!
Is there any place where i can see time limit per problem ?
You can see the time limit and memory limit of each problem in Dashboard. When you submit code in a specific problem, you can see the limit in Submit Code as well.