Hello everyone,
I'm creating this blog post to know about the problems that you once solved and thought to yourself Man I feel amazing after solving this problem. If you remember those favourite problems or you know some problems which requires amazing concepts to learn and you were in awe of the beauty of the problem then post their link in the comments and share them with us.The problem need not be necessarily from codeforces it could be from any judge.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3898 |
| 2 | tourist | 3840 |
| 3 | orzdevinwang | 3706 |
| 4 | ksun48 | 3691 |
| 5 | jqdai0815 | 3682 |
| 6 | ecnerwala | 3525 |
| 7 | gamegame | 3477 |
| 8 | Benq | 3468 |
| 9 | Ormlis | 3381 |
| 10 | maroonrk | 3379 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 165 |
| 3 | Dominater069 | 161 |
| 4 | Um_nik | 159 |
| 4 | atcoder_official | 159 |
| 6 | djm03178 | 157 |
| 7 | adamant | 153 |
| 8 | luogu_official | 150 |
| 9 | awoo | 149 |
| 10 | TheScrasse | 146 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jan/31/2025 10:12:50 (g1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











A few months ago I have come across with this Power Tower problem and I was fascinated by the problem and then learnt a cool trick.
You can check out the problem if you want!
This blog is my favorite one.
One of the most beautiful things that ever happened to me in CP is Factoradic Number!
Using this you can find k-th lexicographically smallest permutation of size n and vice versa in O(nlogn)
You can apply this cool trick in this Misha and Permutations Summation problem.
Happy Coding!
This is a well-known trick but I first discovered it when solving Zebra from Olympiad of Metropolises 2016.
Proof (in the terrible figure below, n = 20)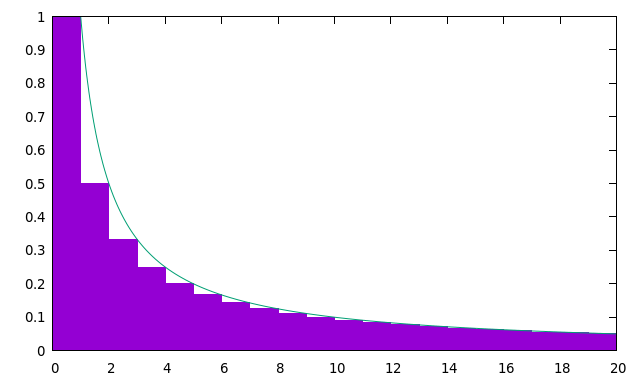
The sum is simply the area covered by the purple boxes. To give an upper bound, we can calculate the area under the green curve, which is piecewise defined as f(x) = 1 for x < 1 and
is simply the area covered by the purple boxes. To give an upper bound, we can calculate the area under the green curve, which is piecewise defined as f(x) = 1 for x < 1 and 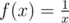 for x ≥ 1. This area is, naturally:
for x ≥ 1. This area is, naturally:
Therefore,
How does this help in solving problems? This gives some algorithms unexpectedly good complexities. For example, suppose you have an array with length n and then you:
divide the array into 1 block and do something with complexity in each block;
complexity in each block;
divide the array into 2 blocks and do something with complexity in each block;
complexity in each block;
divide the array into 3 blocks and do something with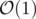 complexity in each block;
complexity in each block;
...
divide the array into n blocks and do something with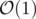 complexity in each block.
complexity in each block.
The total complexity is, magically,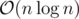 !
!
Here's another fun way to get the approximation by grouping powers of 2 terms:
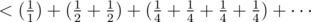
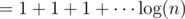 times 1
times 1
Also here you can find an application of this in an expectation problem.
A nice feature of this trick is that you can similarly group the terms of powers of 2 in a different way: , so in fact the sum is
, so in fact the sum is 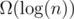 and is thus
and is thus 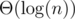 , so this is a totally accurate runtime order, not just an upper bound.
, so this is a totally accurate runtime order, not just an upper bound.
Note that the integral trick also has this property — you can establish a lower bound of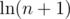 by looking at the function
by looking at the function 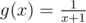 .
.
I liked USACO Censoring (Gold) because I came up with the solution myself (I thought it was quite clever) This is a somewhat well known idea, but I didn't know about it before I came up with it.
There can only be up to sqrt(N) distinct string sizes
When I was learning about dfs, I found 2 very simple questions which can be solved just by dfs and doesn't require any complex idea, just understanding the question and a simple required thought . I found those 2 problems to be quite interesting, even though it might not teach you a lot.
Cycle in Graph
Quantity of Strings
Talking about dfs I found the recent question of lyft round pretty interesting too. Intersecting Subtrees
[fixed the links, were not working earlier]
In recent contests I liked this one - Power tree And its Solution/Proof
This is indeed a good problem. Thank you for showing it to us.
Airport prom ICPC 2017