I have noticed that educational rounds like to use mod 998244353 instead of mod 109 + 7. Does anyone know the reason for this? One idea that comes to mind is since 998244353 < 109 there might be opportunities to troll contestants by breaking division and forcing them to calculate things like 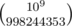 mod 998244353. However I have yet to see this used in an educational round, although this idea was used to good effect in 272D - Dima and Two Sequences.
mod 998244353. However I have yet to see this used in an educational round, although this idea was used to good effect in 272D - Dima and Two Sequences.
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | jiangly | 3976 |
| 2 | tourist | 3815 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3614 |
| 5 | orzdevinwang | 3526 |
| 6 | ecnerwala | 3514 |
| 7 | Benq | 3482 |
| 8 | hos.lyric | 3382 |
| 9 | gamegame | 3374 |
| 10 | heuristica | 3357 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | -is-this-fft- | 165 |
| 3 | Um_nik | 161 |
| 3 | atcoder_official | 161 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 154 |
| 8 | luogu_official | 152 |
| 9 | awoo | 151 |
| 10 | TheScrasse | 147 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2025 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 19.01.2025 01:56:54 (k1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











As far as I know, 998244353 allows you to do interesting stuff related to polynomial multiplication I haven't fully studied yet. See this CF tutorial and this note in Petr's blog.
Other times, 998244353 is used because it's prime, much like 109 + 7, or 109 + 9, or 106 + 69. There can also be a mind-game factor involved: one time, I thought a problem needed the above tricks to be solved simply because the modulo was 998244353, but in the end, I was fooled!
Why it appears often in educational rounds? I don't know, you'll have to ask the setters for that.
This is nice because it lets you do Fast Fourier Transforms (mod p) using only the integers. In other words, the setters don't want to give away whether the problem is supposed to be done using FFT or not.
I think FFT can be done even with modulo 109 + 7. You can do it by FFT with some large two modulos, for example, modulo 1 + 7·226 and 1 + 5·225. Then you can restore the value using Chinese Remainder Theorem (or extended Euclidean algorithm). And finally modulo it by 109 + 7.
Obviously, this way also works for 109 + 9, 998244353, or some other modulos. But, if the modulo is 109 + 7, I think that some people may think "the solution is definitely not FFT" even if FFT is actually involved. Finally, I think taking modulo with 109 + 7 or 109 + 9 is the best way to hide the solution (whether FFT or not).
Recently, problem setters found that giving every problem modulo 998244353 is the best way to hide the solution :( Now 998244353 doesn't mean anything. There are so many problems not using FFT but having modulo 998244353...
Sorry, I wasn't necessarily talking about polynomial multiplication: I agree you can do CRT to do polynomial multiplication mod 109 + 7 say. 998244353 is special because you can actually do a fourier transform with a 2n-th root of unity.
Also, I would say that I also agree that it's just more convenient to have a template to do polynomial multiplication modulo p for any prime p.
desert97 Can you explain what you meant?
I wonder what people will do if I invent an algorithm which only works on mod 696969420...
People won't do this problem since they will get the ultimate orgasm with the first glance.
Just imagine what will happen if people realize there were already some good problems about mod 2!!
usernameson Did you find the reason?
I guess the reason to use 998244353 instead of 10**9+7 is that this hides the answer better... Can't seem to find anything else... This number has again been used in Educational Round 79 (1279D - Santa's Bot)
The FFT answer above made sense to me so I assumed it was correct.
I'm still waiting for 1000696969 to become a popular mod prime.
In china it's more commonly written as (119<<23)+1
Say my question asks mod 10^9 + 7 but I use 998244353 to take advance of the polynomial operations . Now how do I transform my answer back to modulo 10^9+7 ?