Codeforces Round 1133 (Div. 1, Div. 2) is coming soon! Register here. ×

UBERMENSCH.'s blog

Divide Large Number Represented as String

By UBERMENSCH., history, 8 years ago, In English

What are some efficient ways to divide 'a' by 'b' where the range is :

-10^300 <= a,b <= +10^300

  • Vote: I like it
  • +10
  • Vote: I do not like it

»
8 years ago, hide # |
 
Vote: I like it -19 Vote: I do not like it

Since the answer of a/b is between 0 and a, we could use binary_search. Complexity: log(a), which is around 1000.

→ Reply
  • »
    »
    8 years ago, hide # ^ |
     
    Vote: I like it +9 Vote: I do not like it

    That's actually since in every iteration of binary search you need to multiply two numbers.

    Fortunately there's an easier and faster way in O(n2) (hereafter n is the number of digits), assuming the numeric base d is a small constant (typically 2, 10, or 16).

    Start with x = 0, then, for each i from n down to 0, keep incrementing x by di as long as xb ≤ a. This "increment and compare" operation can be done in O(n) by performing it not on x, but on the product xb — you can add bdi to any number by simply appending i zeroes to the d-ary representation of b and performing addition as usual. Running time of this algorithm is O(d·n2). For large values of d you can use binary search inside each iteration of the outer loop, instead of a simple loop which keeps adding di, so the complexity becomes .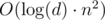

    → Reply
»
8 years ago, hide # |
 
Vote: I like it +23 Vote: I do not like it

There is a way to do it in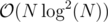 , where N is the sum of lengths of the numbers. Link. But it's masochistic to implement it (as far as I remember).

→ Reply