awoo's blog

Educational Codeforces Round 50 Editorial
By awoo, history, 6 years ago, translation, In English

1036A - Function Height

Tutorial
Solution (Vovuh)

1036B - Diagonal Walking v.2

Tutorial
Solution (Vovuh)

1036C - Classy Numbers

Tutorial
Solution with combinatorics (PikMike)
Solution with precalc (PikMike)

1036D - Vasya and Arrays

Tutorial
Solution (Ajosteen)

1036E - Covered Points

Tutorial
Solution (PikMike)

1036F - Relatively Prime Powers

Tutorial
Solution (PikMike)

1036G - Sources and Sinks

Tutorial
Solution (BledDest)
  • Vote: I like it
  • +44
  • Vote: I do not like it

Comments Comments (39)
| Write comment?
»
6 years ago, # |
← Rev. 2   Vote: I like it +16 Vote: I do not like it

I found a strange thing in F. Two ACs codes output different result. Detail in https://codeforces.me/blog/entry/61728. Can anyone help me?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone prove the author's solution for B?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +1 Vote: I do not like it

    i thought about this problem lot after the contest.

    what i came up with is that there is 8 cases for m,n,k: odd/odd/odd, odd/odd/even....even/even/even. all cases reduce down to the odd/odd/odd case or the even/even/even case. we can see that it is possible to solve the odd/odd/odd or even/even/even case using all diagonal moves as long as m,n is reachable in k moves.

    for an example of "reduction", the even/odd/odd case reduces to the even/even/even case because you can "spend" one non-diagonal move in the n-direction. [1]

    the author's solution is basically "reducing" down all cases to o/o/o or e/e/e cases with mod. see my coded sol here: 42690270

    [1] in fact, the o/o/o case reduces down to the e/e/e case by spending 1 diagonal move

    → Reply
»
6 years ago, # |
  Vote: I like it +26 Vote: I do not like it

Randomized solution for problem G: here

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    cool.

    → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 3   Vote: I like it +12 Vote: I do not like it

    I will try to explain why this solution works: obviously (unless I missed some bug of course, but from conceptual standpoint the solution seems pretty sound), the solution in question can make only one type of mistake: answer "YES" when the actual answer is "NO".

    When the answer is "NO"? When there is at least one "bad" permutation of numbers from 1 to k. I will show that in this cases there are actually a lot more bad permutations than just one. Indeed, consider the set X from the editorial.

    To explain the main idea lets consider the simplest case when |X| = |f(X)|. Then any permutation that matches elements of X only with elements of f(X) and matches elements {1, 2, ..., k} - X with elements {1, 2, ..., k} - f(X) is a bad permutation: when doing a graph walk starting with some source in X, we will never leave reach any source not from X. Therefore there is at least |X|!(k - |X|)! ≥ [k / 2]![(k + 1) / 2]! bad permutations.

    To deal with the case |f(X)| < |X|, we will take some subset Y of X with size |f(X)|, then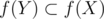 and we can similarly show that all permutations that match sources from Y to sinks in f(X) and sources not from Y to sinks not from f(X) are bad permutations. Therefore there is at least |Y|!(k - |Y|)! ≥ [k / 2]![(k + 1) / 2]! bad permutations.

    All in all, if there is one bad permutation, there are at least [k / 2]![(k + 1) / 2]! of them. So the probability of finding a bad permutation randomly is at least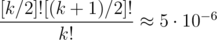 in the worst case of k = 20. From the other hand, on my computer, the code in question checks 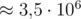random permutations before timing out. In the end, the probability of failure is something of the order  ≈ 10 - 8, which is good enough.

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    cool

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Wasted 1 hour trying to solve a harder version of Problem C. I thought classy numbers were those number which had the number of distinct non zero digits <= 3. And when TC 2 and 3 were not passing, I tried so hard debugging.

After successfully wasting 1 hour, read the question again and BAM!!

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

The data for G maybe too weak? I can easily hack my code.

→ Reply
»
6 years ago, # |
  Vote: I like it +18 Vote: I do not like it

The problem A is so easy, but I solved it late because of my poor English and my poor wi-fi.

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem E, Can anyone please give proof of why exactly GCD + 1 value will give integer co-ordinates?

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

[Deleted]

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In Problem G, it is possible to find for every sources all achievable sinks in a linear time. For this it is necessary to store in each visited vertex an integer (the set of bits of achievable sinks).

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can problem F be solved with some precalculations (generations of correct numbers), simular to problem C?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

there is a easy way to solve problem C with DP :) 42742195

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It seems to be an interesting approach, but I don't really understand it. Could you please explain it briefly?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      f(i,j) means The i th bit of a number(unit's digit,ten's digit...) and already has j non-zero digits.

      DP uses flag to control upper bound.If it is not the upper bound,we can remember the result of f(x,y).(That's why I initialize f to -1 and update f(x,y) when flag=0).f(x,y) will be accessed multiple times, so we can speed it up by remember it .

      My English is poor( I use the google translate QAQ ).

      → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why dont we use -C instead of C? I read in internet that the formula will use -C instead of C? I mean this fragment: long long dx = det(l1.C, l1.B, l2.C, l2.B); long long dy = det(l1.A, l1.C, l2.A, l2.C);

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    By the properties of determinant det(-a, b, -c, d) = det(a, -b, c, -d) = -det(a, b, c, d)

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Ahh it is used then when he does: x = -dx / d; y = -dy / d; right?

      → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why is Problem A tagged with FFT ? Is there a solution with FFT as well ?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Nope, it means an idiot is going around and trolling.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

very very good~ !!

→ Reply
»
6 years ago, # |
  Vote: I like it -6 Vote: I do not like it

E has a tag "fft". Can it be done using FFT too? If yes, then how?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For problem 1036E — Covered Points , can anybody explain what's special with the test 14? I've seen some people failing this test.

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Could someone explain how mobius function could be used in problem F. All I understood is that we are trying to remove the bad elements from the answer. Basically, could someone explain me the formula?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

in problem G, how about a 4-vertex graph: 1->2, 3->2, 3->4 ??? It's obvious that 1 is a source but the set of sink it can reach is just {2}???

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

is there a proof for problem b ?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain the brute force generation for C

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    pos represents the number of digits,cnt represents count of non-zero digits and cur represents the value generated. first we take the generated number and multiply by 10 and increasing number of digits. if a number is classy number then its multiple of 10 will also be a classy number. then we check if the number has less than 3 non-zero digits or not.if it has less than 3 non-zero digits then we can put any number between 1 to 9 at units place and generate another classy number(multiply by 10 and adding the number). we also increase the count of non-zero digit.

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I was really confused. thanks for the explanation.

      → Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

please can anyone explain the formula in problem C, i dont know why it return exactly the beautiful numbers on [1,X), why cur-- like that, that means for(int cur = 3; cur>=0; cur --) , i think i'll insert s[i] in a set so that its size is cur ... A lot of things i cant understand. I've read PikMike's code and the formula for hours. Help me please.

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Proof why GCD works in E

→ Reply
»
5 years ago, # |
  Vote: I like it +26 Vote: I do not like it

The solution to G reminds me of Hall's marriage theorem, and I finally figured out how to solve it in polynomial time.

Take the graph of sources and reachable sinks. If no perfect matching exists, by Hall's marriage theorem, there is a nonempty proper subset of sources $$$X$$$ such that $$$|X|>|f(X)|$$$, so the answer is NO. Otherwise, we need to ensure that $$$|X|<|f(X)|$$$. This means $$$f(X)$$$ has sinks besides the ones matched to sources in $$$X$$$. Connect each sink to the source it is matched to in the perfect matching. The answer is YES if and only if the the resulting graph is strongly connected.

Code: 67053099

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone explain F with little more details ?

→ Reply